На каждой ступеньке записано задание в одно действие. Класс делится на команды по 6 человек. Каждый ученик решает по очереди свой пример, и записывает ответ на своей «ступеньке». Шестой ученик ответы складывает. Результат записывает в треугольник.
0,7+8= ?
11,2+4=
7,3+6,7= +
+
0,3+5=
+
1,5+2,3= +
3. Работа по теме урока
3.1. №1203 (устно)
3.2. №1207 (у доски)
3.3. №1211 (2 человека у доски, остальные в тетрадях)
3.4. Задание на карточке
4. Домашнее задание №1236(в, г) №1240
5. Итог урока. Самостоятельная работа
Самоанализ
На уроке была использована групповая форма работы. Сообщены тема и цели урока. Время на уроке распределено. Устные упражнения проведены в форме игры «Умная лесенка». Это задание заинтересовало всех детей без исключения. Во время игры дети активно решали примеры, чтобы как можно быстрее решить пример и передать эстафету другому ученику. Групповая форма помогла организовать детей. Во время игры развивала умение работать в группе. Данная игра настроила детей на работу. На уроке были использованы разные виды проверки, формы организации работы учащихся. Учащиеся работали активно, поэтому поставленные цели реализованы. План был выполнен. Итог урока подведен. Самостоятельная работа дала следующие результаты: «5»- 12, «4»- 8, «3»- 4, «2»-нет.
Конспект урока по теме «Сложение и вычитание десятичных дробей»
Цели урока: - закрепление навыков сложения и вычитания десятичных дробей при решении задач «на движение по реке»;
- развитие вычислительных навыков, математической речи;
- воспитание интереса к предмету.
Оборудование: карточки для игры, для работы по теме урока, индивидуальные карточки.
Ход урока
1. Сообщение темы и целей урока
2. Устные упражнения. Игра «Сигнальное устройство»
Перед вами сигнальное устройство, которое пропускает только карточки с верными равенствами. Запишите последовательно буквы с «верных карточек», то есть с тех, которые пройдут через устройство. Прочитать полученное слово и что оно обозначает.
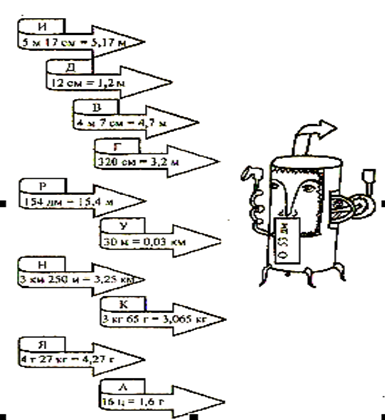
Полученное слово является названием самой маленькой в мире обезьянки. Выразите ее длину в сантиметрах, а массу в граммах:
длина: 0,23 м=23см
масса: 0,05 кг=50 г.
Ответ: Игрунка
3. Изучение нового материала
3.1. Объяснение учителем
3.2. №1193 (у доски)
3.2. Работа с карточками
4. Домашнее задание №1235 №1239 №1241
5. Итог урока (индивидуальные карточки с задачами).
Самоанализ
На уроке были использованы метод объяснения нового материала учителем. Сообщены тема и цели урока. Время на уроке распределено. Устные упражнения проведены в форме игры «Сигнальное устройство». Игра заинтересовала всех детей без исключения. Во время игры дети активно решали примеры, чтобы узнать какую длину и массу тела имеет самая маленькая в мире обезьянка. Большинство учеников пришли к правильному ответу, но некоторые не могли перевести сантиметры в метры. Игра носит познавательный характер, так как во время игры дети получают дополнительные знания. Данная игра настроила детей на работу. На уроке были использованы разные виды проверки, формы организации работы учащихся. Учащиеся работали активно, поэтому поставленные цели реализованы. План был выполнен. Итог урока подведен.
Конспект урока по теме « Приближенные значения чисел. Округление чисел»
Цели урока: - знакомство с округлением чисел, записью приближенных значений числа с недостатком и с избытком;
- развитие вычислительных навыков, математической речи;
- воспитание аккуратности, интереса к предмету.
Оборудование: карточки для игры
Ход урока
1. Сообщение темы и целей урока
2. Устные упражнения Игра «В мире животных»
В нашей стране водится много бобров. Бобр – крупный грызун, ведет полуводный образ жизни, обитает по лесным рекам, сооружает из ветвей и ила домики, поперек реки делает плотины длиной 5-6 метров. Узнать длину тела бобра (в дециметрах) поможет вам удивительный квадрат:
| 5,9 | 6,3 | 3,6 |
| 2,3 | 2,7 | 0 |
| 3,7 | 4,1 | 1,4 |
1. Из первой строки выберите наименьшее число [3,6].
2. Из второй строки выберите наибольшее число [2,7].
3. Из третьей строки выберите не наименьшее и не наибольшее число [3,7].
4. Найдите сумму выбранных чисел – и вы получите ответ на вопрос [10дм=1м].
3. Математический диктант
4. Изучение нового материала
5. Закрепление изученного материала
5.1. №1243 (устно)
5.2. №1245 (по цепочке у доски)
5.3. №1247 (а - мальчики, б - девочки)
6. Домашнее задание: №1271 №1273 (а,б) №1274
7. Итог урока (вопросы после параграфа)
Самоанализ
На уроке были использованы метод объяснения нового материала учителем. Сообщены тема и цели урока. Устные упражнения проведены в форме игры «В мире животных». Во время игры дети активно решали примеры, чтобы узнать какую длину тела имеет бобр. Большинство учеников пришли к правильному ответу, но некоторые не могли перевести дециметры в метры. Игра носит познавательный характер, так как во время игры дети получают дополнительные знания. Данная игра настроила детей на работу. На уроке были использованы разные виды проверки, формы организации работы учащихся. Учащиеся работали активно, поэтому поставленные цели реализованы. Этапы урока распределены по времени. Проводились микрообобщения после каждого пункта плана. Итог урока подведен.
Конспект урока по теме «Приближенные значения чисел. Округление чисел»
Цели урока: - закрепление умения округлять числа, записывать приближенные значения чисел с недостатком и с избытком;
- развитие вычислительных навыков, математической речи;
- воспитание интереса к предмету, аккуратности.
Оборудование: карточки для игры, для самостоятельной работы.
Ход урока
1. Сообщение темы и целей урока
2. Устные упражнения. Игра «Смотри, не зевай, быстро считай»
Учащиеся делятся на две команды. Участники команд прикалывают на грудь номера от 0 до 9. У первой команды номера синего цвета (из разряда единиц). У второй команды номера цифр зелёного цвета (из разряда десятых). У доски стоят два стула. Каждый из играющих считает и думает, входит ли его число в ответ или нет. «Единицы» садятся на свой стул, «десятые» - на свой.
Если ответ правильный и члены команд сели одновременно, то им присуждается по 1 баллу. Если одна из команд выполнила задание позже, то она не получает баллов. Запомнить на слух трудно, поэтому примеры автор писала на табличках и показывала детям.
Примеры: 1) 4,7+2,9; 2) 6,3+3,5; 3) 8,5 + 0,8; 4) 2,3 + 0,9; 5) 7,4+2,3; 6) 4,2 + 3,4;
7) 1,3 + 0,4; 8) 1,8 + 3,5; 9) 3,4 + 1,7; 10) 5,6 + 3,9.
3. Работа по теме урока
3.1. № 1246 (у доски)
3.2. № 1248 (самостоятельно)
3.3. № 1249 (на оценку у доски)
3.4. №1267 (на 4 варианта)
4. Самостоятельная работа
5. Домашнее задание: №1270 № 1273 (в, г) № 1272(а, б).
6. Итог урока (рефлексия)
Самоанализ
Сообщены тема и цели урока. Время на уроке распределено. Устные упражнения проведены в форме игры « Смотри, не зевай, быстро считай». Это задание заинтересовало всех детей без исключения. Во время игры дети активно решали примеры, чтобы как можно быстрее прибежать на свой стул. Большинство учеников пришли к правильному ответу, но некоторые не могли долго сосчитать. Игра носит познавательный характер, так как во время игры дети стремились быть первыми, им было интересно. Данная игра настроила детей на работу. На уроке были использованы разные виды проверки, формы организации работы учащихся. Учащиеся работали активно, поэтому поставленные цели реализованы. План был выполнен. Итог урока подведен.
Конспект урока по теме «Приближенные значения чисел. Округление чисел»
Цели урока: - развитие познавательного интереса учащихся
путем использования дидактических игр на уроке;
- формирование умения выполнять арифметические действия
с десятичными дробями;
- формирование умения работать в парах и микрогруппах;
- воспитание интереса к предмету.
Оборудование: карточки
Ход урока
1.Устная работа.
Сегодня мы с вами отправимся в путешествие. Путь наш лежит в средневековый город на рыцарский турнир.
Перед дальней дорогой необходимо подкрепиться. А так как мы отправимся в математический город на математический рыцарский турнир, то нам необходимо подкрепиться знаниями.
Повторение теории по пунктам 30-32 учебника.
Вопросы: 1). Какие обыкновенные дроби можно записать в виде десятичных дробей?
2). Как определить количество цифр после запятой в десятичной записи
дроби?
3).Назовите первые 4 разряда после запятой в десятичных дробях.
4). Сформулируйте правило сложения (вычитания) десятичных дробей.
5). Сформулируйте правило сравнения десятичных дробей.
Хорошо, молодцы!Ну, а теперь можно и в путь!
2.Игра: «Рыцарский турнир».
1). Попасть в средневековый город непросто. Чтобы преодолеть временное пространство, необходимо пройти через математический лабиринт.
Время на прохождение лабиринта у вас ограничено; первые три человека, прошедшие лабиринт будут тремя рыцарями –участниками рыцарского турнира, все остальные – это их команда.
Учащимся предлагается задание «Математический лабиринт»
Математический лабиринт.
Вход в лабиринт: задание № 1
Выход из лабиринта: ответ совпадает с номером задания.
№ 1. Выполните действия: 8,65 - 5,7 + 1,05
№ 2. Решите уравнение: ( х + 1,7 ) – 3,3 = 0,4
№ 3. Решите задачу:
Расстояние между городами 120 км. Из городов навстречу друг другу одновременно выехали два велосипедиста со скоростью 13,6 км/ч и 10,4 км/ч соответственно. Через сколько часов они встретятся?
№ 4. Найдите периметр треугольника АВС, если АВ = 0,4 м, ВС больше АВ на 0,65 м, но меньше АС на 0,5 м.
№ 5. Вычислите: ( 24,67 + 15,33 ) : ( 88,9 – 68,9 )
( Примечание: Ключ к лабиринту: № 1 № 4 № 3№ 5 № 2 ).
2). Рыцарский турнир: «Кто быстрее?». Математическая эстафета.
Бланк с заданием получают ученики, сидящие за первой партой. Каждый решает одно задание и передает назад. Ученики, сидящие за последней партой, называют окончательный ответ.
1 вариант.
|
| |
+ 2,8 + 4,9 + 2,4 : 2
2 вариант.
|
| |
+ 1,8 12 + 1,3 - 5,3
3).2.рыцарский турнир: «Кто дальше?».
Рыцари – участники соревнования по стрельбе из лука. Сначала с помощью жеребьевки определяем номер лука. Далее надо найти значение выражения, соответствующего данному номеру. Полученный ответ будет определять дальность полета стрелы каждого участника. Отметив положение стрелы на числовом луче, определите, кто победил!
Каждая парта получает бланк с соответствующим заданием. На доске (или с помощью кодоскопа) изображен числовой луч, на котором цветными магнитами первые выполнившие задание отмечают полученные числа.
Бланк с заданием:
II рыцарский турнир:«Кто дальше? ».
1). Методом жеребьевки определите номер своего лука со стрелой.
2). Найдите значение выражения соответствующего указанному номеру.
3). Полученный ответ определяет дальность полета стрелы каждого
участника.
4).Отметив положение стрелы на координатном луче, определите, кто победил.
№ 1. ( 6.42 + 4,9 ) + ( 17,26 – 16,08 )
№ 2. 2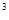 
+ ( 2,82 + 4,36 ) – ( 0,67 + 3,41 )
№ 3. ( 25,9 - 6,2 ) – ( 19,374 + 4,626) : 3
№ 4. ( 42,75 – 37,26 ) + ( 17,32 – 12,31 ) + 
№ 5. 3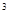 
- ( 6,03 + 4,27 ) – ( 3,7 + 1,2 ) -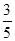 
4). 3. рыцарский турнир: «Самый зоркий».
Расшифруй слово. Что оно означает?
Учащиеся получают бланк с заданием, на котором зашифровано два слова (1 и 2 варианты).
Ответы: Мицар и Алькор - звезды в созвездии Большой медведицы.
С помощью кодоскопа рассмотреть изображение Большой медведицы и расположение указанных звезд.
Бланк с заданием:
III рыцарский турнир: «Самый зоркий!».
1 вариант.
Расшифруйте слово! Что оно обозначает?
Ц 12,1 – ( х + 5.8 ) = 1,7
Р( у – 3,7 ) – 1,8 = 4,7
М ( 2,9 + х ) – 3,5 = 4,5
И14,08 – ( 52,3 – х ) = 1,003
А 6,793 х + 0,007 х +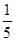 
х = 7042
| 5,1 | 39,223 | 4,6 | 1006 | 10,2 |
2 вариант.
Расшифруй слово! Что оно обозначает?
Р ( у – 3,7 ) – 1,8 = 4,7
Ь 13,2 - ( 5,7 + х ) = 3,9
О ( 39,4 – х ) + 2,004 = 27,03
А 6,793 х + 0,007 х +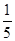 
х = 7042
К 3,97 х + 20, 4 х + 0,63 х = 5050
Л ( 52,3 – х ) – 4,08 = 17,3
| 1006 | 30,92 | 3,6 | 202 | 14,374 | 10,2 |
4.. Итог урока.
Ну, вот и закончился рыцарский турнир. Победитель -
В ходе нашей игры мы повторили сложение и вычитание десятичных дробей, решение уравнений, построение точки на числовом луче.
Пора возвращаться домой из средневековья. Но чтобы вернуться, нужно разгадать анаграммы:
ТАМЕЛЬНАЗЕН (знаменатель)
ИЛЕТСИЧЛЬ(числитель)
ИНОЖЕЛЕС (сложение)
ИВЕТЫЧАНИ(вычитание)
ОДАНОТИКАР(координата)
БОРЬД(дробь)
Молодцы!
5. Домашнее задание (подготовиться к контрольной работе).
Самоанализ
Урок-игра «Рыцарский турнир» начинается с устной работы, где идет объяснение правил игры. Четко были сформированы тема, цели и тип урока. Все учащиеся были хорошо подготовлены к уроку, легко включались в работу. На уроке использовалась наглядность, кодоскоп. Время было распределено рационально. Все учащиеся были вовлечены в работу. При помощи игр у детей автор развивала внимание, память, интерес к математике через использование различных видов заданий. Чередовались письменные виды деятельности с устными. За счет смены видов деятельности обеспечивалась высокая работоспособность учащихся на уроке. Урок был эмоционален и спокойно завершен.
Таким образом, применение дидактических игр на уроках помогает добиться того, чтобы каждый ученик работал активно и увлеченно, используя игру как отправную точку для возникновения и развития любознательности, глубокого познавательного интереса. Подобранные игры способствуют развитию у учащихся памяти, внимания, наблюдательности, интереса. В этих играх важным стимулом является элемент соревнования, так как в соревнованиях проявляются активность ученика и воля к победе. Дидактические игры хорошо сочетались с серьезным учением.
2.2. Опытно-экспериментальная работа. Анализ ее результатов
Для подтверждения гипотезы и выполнения поставленных задач была проведена экспериментальная работа, которая проходила в три этапа:
1) Констатирующий эксперимент.
2) Формирующий эксперимент
3) Контрольный эксперимент.
Цель исследования: убедиться в эффективности использования различных видов дидактических игр для развития познавательного интереса на уроках математики.
Исследование проходило на базе Опачевской школы Ординского района. Были взяты два класса: 5а - экспериментальный и 5б – контрольный.
В 5а классе учатся 24 человека: 11 мальчиков и 13 девочек. Класс занимается по учебнику Виленкина Н.Я.Математика 5 класс.
В 5б классе учатся 18 человек: 10 мальчиков и 8 девочек. Класс также занимается по учебнику Виленкина Н.Я. Математика 5 класс.
1. Констатирующий эксперимент.
Цель: выявить, на сколько дети активны и заинтересованы на уроках математики на исходном этапе эксперимента.
1.1. Анкетирование экспериментального класса
Учащимся была предложена следующая анкета:
Фамилия, имя
1) какой предмет в школе тебе больше всего нравится?
2) Ты быстрее решаешь устно или письменно?
3) Нравится ли тебе, когда на уроке математики проводят игры?
4) Тебе больше нравится выполнять задания по русскому языку, литературе или по математике?
5) На какой бы урок ты опоздал? (русский, математика, литература)
Основное внимание при анализе анкет учащихся уделялось 1 и 5 вопросам, 3 и 4, 2 вопросы дополняли ответ. Проанализировав протокол, были выявлены следующие результаты.[См.приложение 2]
При ответе на первый вопрос не всем учащимся нравятся уроки математики. 58% учащихся больше всего нравится математика, 9% - ИЗО, еще 9% нравится технология,12% нравится история и также 12% нравится русский язык. Таким образом, не всем учащимся легко заниматься математикой.
Результаты второго вопроса были следующими: 71% учащихся быстрее решают устно, чем письменно; 29% учащихся быстрее решают письменно, чем устно.
Ответы на третий вопрос были такими: 90% учащихся нравится, когда с ними проводят игры, 10% - не нравится, когда с ними проводят игры.
Результаты четвертого вопроса были такими: 50% учащихся больше всего нравится выполнять задания по математике, 29% –нравится выполнять задания по русскому языку, 21% - нравится выполнять задания по литературе. Можно сказать, что половина учащихся этого класса не заинтересована в математике.
Ответы пятого вопроса: 33% учащихся – прогуляли бы математику, 46% - русский язык, 21% - прогуляли бы литературу.
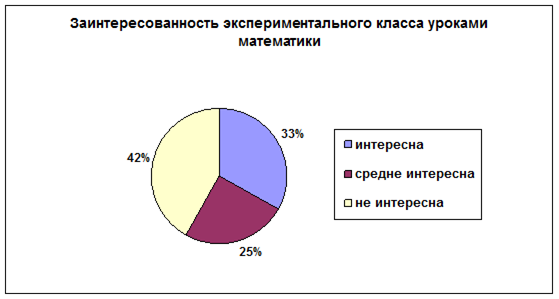
Таким образом, у 33% учащихся экспериментального класса высокая заинтересованность в математике. Учащимся нравятся уроки математики, они активны на уроке, им нравится выполнять различные задания по математике, никогда бы не пропустили урок математики.
25% учащихся экспериментального класса имеет средний уровень заинтересованности в математике. На уроках учащиеся активны, но требуют систематических побуждений учителя. При разборе трудных вопросов прибегают к помощи учителя. Самостоятельное выполнение зависит от ситуации, наличия побуждения учителем или товарищем. Трудности преодолевают с помощью других.
У 42% учащихся экспериментального класса низкий уровень заинтересованности в математике. Учащимся не нравятся уроки математики, наблюдается познавательн6я инертность. Не стремятся разобраться в трудных вопросах. Мнимая самостоятельность действий (списывание с доски, у соседа по парте), частые отвлечения. Полная бездеятельность при затруднениях, отсутствие интереса к математике.
Дата: 2019-12-22, просмотров: 426.
