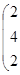
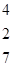
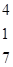
Однородный продукт, сосредоточенный в 3 пунктах производства (хранения) в количествах 40; 60; 70 единиц, необходимо распределить между 4 пунктами потребления, которым необходимо соответственно 36; 32; 40; 53 единиц. Стоимость перевозки единицы продукта из пункта отправления в пункт назначения известна для всех маршрутов и равна С = 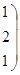. Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были минимальными.

Для решения транспортной задачи чаще всего применяется метод потенциалов.

Общий объем производства åа_i =40+60+70=170 больше, чем требуется всем потребителям åb_i = 36+32 +40 +53 =161, т.е. имеем открытую модель транспортной задачи. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления 170-161 = 9 единиц, причем тарифы на перевозку в этот пункт условимся считать равными нулю, помня, что переменные, добавляемые к левым частям неравенств для превращения их в уравнения, входят в функцию цели с нулевыми коэффициентами.

Первое базисное допустимое решение легко построить по правилу ²северо-западного угла².

Потребление	b1 =36	b2 =32	b3 =40	b4 =53	b5 =9
Производство
а1 =40	36	4				p1 =0
a2 =60		28	32			p2 =
a3 =70	*		8	53	9	p3 =
	q1 =	q2 =	q3 =	q4 =	q5 =

Общая стоимость всех перевозок для первого базисного допустимого решения:

L = 36* 2 + 4 *3 + 28 *2 + 32 + 8* 7+ 53 =281

Один из потенциалов можно выбрать произвольно, так как в системе (3), (4) одно уравнение линейно зависит от остальных. Положим, что р₁ = 0. Остальные потенциалы находим из условия, что для базисных клеток 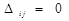. В данном случае получаем

        D₁₁ = 0,      p₁ + q₁ - c₁₁ = 0,     0+q₁ -2 = 0, q₁ = 2

        D₁₂ = 0,      p₁ + q₂ - c₁₂ = 0,     0+q₂ -3 = 0, q₂ = 3

D₂₂ = 0,       p₂ + q₂ - c₂₂ = 0,     р₂ +3-2 = 0, р₂ = -1

и т.д., получим: q₃=2, p₃=5, q₄= -4, q₅= -5.

Затем по формуле (6) вычисляем оценки всех свободных клеток:

        D₂₁ = p₂ + q₅ - c₂₁ = -1+2-4 = -3

        D₃₁ = p₃ + q₁ - c₃₁ = 5+2-2 = 5

        D₃₂ = 1; D₁₃ = -2; D₁₄ = -5; D₂₄ = 0; D₁₅ = -5; D₂₅ = -6.

Находим наибольшую положительную оценку max ( 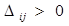) = 5 =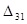

Для найденной свободной клетки 31 строим цикл пересчета - замкнутую ломаную линию, соседние звенья которой взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке, а все остальные - в занятых клетках. Это будет 31-11-12-22-23-33. Производим перераспределение поставок вдоль цикла пересчета

36	4			36-r	4+r			28	12
	28	32			28-r	32+r			20	40
		8		r		8-r		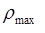8

= 8

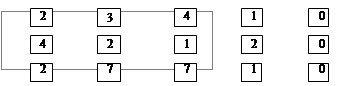
Получаем второе базисное допустимое решение:

bj	b1 =36	b2 =32	b3 =40	b4 =53	b5=9
ai
а1 =40	28	12		*		p1 =0
a2 =60		20	40			p2 = -1
a3 =70	8			53	9	p3 =0
	q1 =2	q2 = 3	q3 = 2	q4 = 1	q5=0

Находим новые потенциалы, новые оценки.

D₁₃ = -2; D₁₄ = 0; D₁₅ = 0; D₂₁ = -3; D₂₄ = -2; D₂₅ = -1; D₃₂ = -4; D₃₃ = -5,

т.е. все D_ij £ 0 i = 1,m; j = 1,n

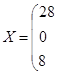
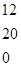
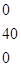
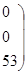
 Общая стоимость всех перевозок для второго базисного допустимого решения:

L = 28* 2 + 12 *3 + 20 *2 + 40 + 8* 2+ 53 =241 – минимальная стоимость.