КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

КУРСОВАЯ РАБОТА

по дисциплине "Прикладная математика"

Москва 2001

ОГЛАВЛЕНИЕ

ЛИНЕЙНАЯ ПРОИЗВОДСТВЕННАЯ ЗАДАЧА

ДВОЙСТВЕННАЯ ЗАДАЧА

ЗАДАЧА О "РАСШИВКЕ УЗКИХ МЕСТ ПРОИЗВОДСТВА"

ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. РАСПРЕДЕЛЕНИЕ КАПИТАЛЬНЫХ ВЛОЖЕНИЙ

ДИНАМИЧЕСКАЯ ЗАДАЧА УПРАВЛЕНИЯ ПРОИЗВОДСТВОМ И ЗАПАСАМИ

МАТРИЧНАЯ МОДЕЛЬ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ПРЕДПРИЯТИЯ

МАТРИЧНАЯ ИГРА КАК МОДЕЛЬ КОНКУРЕНЦИИ И СОТРУДНИЧЕСТВА

АНАЛИЗ ДОХОДНОСТИ И РИСКА ФИНАНСОВЫХ ОПЕРАЦИЙ

ЗАДАЧА ФОРМИРОВАНИЯ ОПТИМАЛЬНОГО ПОРТФЕЛЯ ЦЕННЫХ БУМАГ

ЛИТЕРАТура

ДВОЙСТВЕННАЯ ЗАДАЧА

Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.

Теперь представим себе, что знакомый предприниматель П, занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у₁ рублей за каждую единицу первого ресурса, у₂ руб – второго, у₃ руб – третьего. Возникает вопрос: при каких ценах у₁, у₂, у₃ мы можем согласиться с предложением П.

Величины у₁, у₂, у₃ принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.

Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имели вид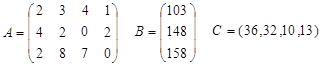

Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 2 единицы ресурса первого вида, 4 единицы ресурса второго вида и 2 единицы третьего (элементы первого столбца матрицы). В ценах у₁, у₂, у₃ наши затраты составят 2у₁+ 4у₂+ 2у₃, т.е. столько заплатит предприниматель П за все ресурсы, идущие на производство единицы продукции первого вида. На рынке за единицу первой продукции мы получили бы прибыль 36 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше 2у₁+ 4у₂+ 2у₃³ 36.

Аналогично, для трех оставшихся видов продукции:

3у₁+ 2у₂+ 8у₃³32

4у₁+ 7у₃³10

у₁+ 2у₂ ³13

Учтем, что за все имеющиеся у нас ресурсы нам должны заплатить 103у₁+ 148у₂+ 158у₃ рублей. При поставленных нами условиях предприниматель П будет искать такие значения величин у₁, у₂, у₃, чтобы эта сумма была как можно меньше. Подчеркнем, что здесь речь идет не о ценах, по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.

Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок у(у₁, y₂, y₃) минимизирующий общую оценку всех ресурсов f = 103у₁+ 148у₂+ 158у₃(1)

при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции

2у₁+ 4у₂+ 2у₃³ 36

3у₁+ 2у₂+ 8у₃³32 (2)

4у₁+ 7у₃³10

у₁+ 2у₂ ³13

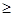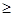причем оценки ресурсов не могут быть отрицательными y₁ 0, y₂ 0, y₃ 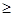0. (3)

Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений 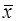(х₁, х₂, х₃, х₄) и 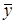(y₁, y₂, y₃) пары двойственных задач необходимо и достаточно выполнение условий

x ₁ (2у₁+ 4у₂+ 2у₃- 36) = 0 y₁ (2x₁ +3x₂+ 4x₃+ x₄- 103) = 0

x ₂ (3у₁+ 2у₂+ 8у₃- 32) = 0 y₂ (4x₁ +2x₂ + 2x₄- 148) = 0

x ₃(4у₁+ 7у₃- 10) = 0 y₃ (2x₁ +8x₂+ 7x₃- 158) = 0 .

x ₄(у₁+ 2у₂ - 13) = 0

Ранее было найдено, что в решении исходной задачи х₁>0, x₂>0. Поэтому

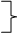2y₁+ 4y₂+ 2y₃ - 36 = 0

3y₁+ 2y₂+ 8y₃- 32 = 0

Если же учесть, что первый ресурс был избыточным и, согласно той же теореме двойственности, ее двойственная оценка равна нулю у₁=0,

то приходим к системе уравнений

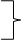4y₂+ 2y₃ - 36 = 0

2y₂+ 8y₃- 32 = 0

откуда следует у₂=8, у₃=2.

Таким образом, получили двойственные оценки ресурсов у₁=0; у₂=8; у₃=2, (4)

причем общая оценка всех ресурсов равна 1500.

Заметим, что решение (4) содержалось в последней строке последней симплексной таблицы исходной задачи. Важен экономический смысл двойственных оценок. Например, двойственная оценка третьего ресурса у₃=2 показывает, что добавление одной единицы третьего ресурса обеспечит прирост прибыли в 2 единицы.

ЗАДАЧА О "РАСШИВКЕ УЗКИХ МЕСТ ПРОИЗВОДСТВА"

При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, т.е. образуют ² узкие места производства ² . Будем их заказывать дополнительно. Пусть T(t₁,t₂,t₃)- вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие H + Q^-1T 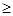0.

Задача состоит в том, чтобы найти вектор T (0, t₂, t₃), максимизирующий суммарный прирост прибыли W = 8t₂ + 2t₃ (1) при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)

(2)

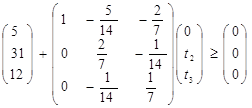
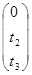
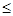
предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида 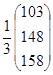(3)

причем по смыслу задачи t₂ 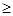0, t₃ 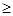0. (4)

Переписав неравенства (2) и (3) в виде:

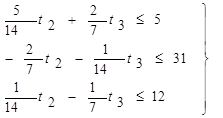(5)

из условия (3) следует t2£148/3, t3£158/3 (6)

приходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).

Эту задачу легко решить графически: см. рис. 2. Программа ²расшивки² имеет вид

t₁=0, t₂=14, t₃=0 и прирост прибыли составит 112.

Сводка результатов приведена в таблицe 2.

с_j	36	32	10	13	b	x_4+i	y_i	t_i
	2	3	4	1	103	5	0	0
a_ij	4	2	0	2	148	0	8	14
	2	8	7	0	158	0	2	0
xj	31	12	0	0	1500			112

D_j	0	0	4	3

Таблица 2

 - x2 0 100 200 300 400 500 600 700

x2 F1( - x2)

F2(x2) 0 15 24 30 36 40 43 45

0 0 15 24 30 36 40 43 45

100 18 18* 33* 42* 48 54 58 61

200 26 26 41 50* 56 62 66

300 34 34 49 58* 64* 70*

400 39 39 54 63 69

500 42 42 57 66

600 44 44 59

700 46 46

Таблица 3

 0 100 200 300 400 500 600 700

F2() 0 18 33 42 50 58 64 70

 ()

0 0 100 100 200 300 300 300

Таблица 4

 - x3 0 100 200 300 400 500 600 700

x3 F2( - x3)

F3(x3) 0 18 33 42 50 58 64 70

0 0 18* 33 42 50 58 64 70

100 16 16 34* 49* 58 66 74 80

200 27 27 45 60* 69 77 85

300 37 37 55 70* 79* 87*

400 44 44 62 77 86

500 48 48 66 81

600 50 50 68

700 56 56

Таблица 5

 0 100 200 300 400 500 600 700

F3() 0 18 34 49 60 70 79 87

()

0 0 100 100 200 300 300 300

Таблица 6

 - x4 0 100 200 300 400 500 600 700

x4 F3( - x4)

F4(x4) 0 18 34 49 60 70 79 87

0 0 87

100 10 89*

200 17 87

300 23 83

400 29 78

500 34 68

600 38 56

700 41 41 .

Наибольшее число на этой диагонали: Zmax = 89 тыс. руб.,

причем четвертому предприятию должно быть выделено х*4 = 4 (700) = 100 тыс. руб.

На долю остальных трех предприятий остается 600 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено x*3 = 3 (700-x*4) = 3 (600) = 300 тыс. руб.

Продолжая обратный процесс, находим x*2 = 2 (700 - x*4 - x*3) = 2 (300) = 100 тыс. руб.

На долю первого предприятия остается x*1 = 700 - x*4 - x*3 - x*2 = 200 тыс. руб.

Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:

x*1 =200; x*2 =100; x*3 = 300; x*4 = 100.

2 11 18 29 42 57

x1(=y2) 0 1 2 3 4 5

Переходим ко второму этапу. Полагаем k = 2 и табулируем функцию F2( = y3)

Или 3 3

Переходим к следующему этапу. Полагаем k=3 и табулируем функцию F3 ( = y4):

Вычисляем значение функции состояния только для одного значения аргумента  = у4 = 0, так как не хотим оставлять продукцию в запас в конце исследуемого периода.

0y40; =y4; 0  x3  d3 + y4 → 0  x3  3; y3 = y4 + d3-x3= y4+3- x3;

3(x3, y4) = a + bx3 + c + h3y4 + F2(y3)= +2 x3+2 + 2 y4 + F2(y3)

x3=0 y3=3 3(0;0)=02 + 20 +2 +20 +F2(3)=2 +44=46

x3=1 y3=2 3(1;0)=12 + 21 +2+20 + F2(2)=5 +34=39

x3=2 y3=1 3(2;0)=22 + 22 +2+20 + F2(1)=10+22=32*

x3=3 y3=0 3(3;0)=32 + 23 +2+20 +F2(0)=17 +18=35

Получаем F3 ( = y4) = min 3 (x3,0) = 32, причем минимум достигается при  3 ( = y4 = 0) = 2.

Таким образом, мы получили не только минимальные общие затраты на производство и хранение продукции, но и последнюю компоненту оптимального решения. Она равна = 2.

Остальные компоненты оптимального решения найдем по обычным правилам метода динамического программирования. Чтобы найти предпоследнюю компоненту, учтем, что х3 + у3 - -d3 = y4 или 2 + у3 - 3 = 0, oткуда у3 = 1. Из таблицы (2) значений находим

Аналогично, продолжая двигаться в обратном направлении и учтя, что х2 + у2 - d2 = y3 или 3 + у2 - 2 = 1, получаем у2 = 0; из таблицы (1) значений х1() находим .

Итак, оптимальный план производства имеет вид х1 = 0, х2 = 3, х3 = 2, а минимальные общие

Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку и цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками. Почти всегда финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль так и убыток (или не очень большая прибыль по сравнению с той, на что надеялись проводившие эту операцию). Существует несколько разных способов оценки операции с точки зрения ее доходности и риска. Наиболее распространенным является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.

Даны четыре операции Q1, Q2, Q3, Q4. Найдите средние ожидаемые доходы и риски ri операций. Нанесите точки ( , ri) на плоскость, найдите операции, оптимальные по Парето. С помощью взвешивающей формулы найдите лучшую и худшую операции. Взвешивающая формула одна и та же:

(Q) = 2 - r.

Q1 : 2 4 6 18

1/2 1/4 1/8 1/8

Q2 : 0 4 6 12

1/4 1/4 1/3 1/6

Q3 : 2 5 8 14

ј ј 1/3 1/6

: 0 1 2 8

1/3 1/3 1/6 1/6

Q1 = qipi = 2*1/2+4*1/4+6*1/8+18*1/8=5

Q21 = 25

M [Q21] = 4*1/2+16*1/4+36*1/8+324*1/8=51;

Q2 = 1+2+2=5

Q22 = 25

M [Q22] = 16*1/4+36*1/3+144*1/6=40;

Q3 = 2+5=7

Q23 = 49

M [Q23] = 4*1/4+36*1/4+64*1/3+196*1/6=64;

Q4 = 2

Q24 = 4

M [Q24] = 1*1/3+4*1/6+64*1/6=70/6;

Нанесем средние ожидаемые доходы Q и риски r на плоскость - доход откладываем по горизонтали, а риски по вертикали (см. рис.):

Получили 4 точки. Чем правее точка (Q, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (Q, r) доминирует точку (Q, r) если Q Q и r  r.

Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар (Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть  (Q)= 2Q - r . Тогда получаем:

 (Q1)= 2*5-5,1 = 4,9;  (Q2)= 2*5-3,9=6,1;  (Q3)= 2*7-3,9=10,1;  (Q4)= 2*2-2,8=1,2

ЛИТЕРАТУРА

1. Математические методы принятия решений в экономике. Учебник под ред. проф. Колемаева В.А. -М.: ЗАО "Финстатинформ", 1999.

Ершов А.Т., Карандаев И.С., Шананин Н.А. Планирование производства и линейное программирование. МИУ, М., 1981.