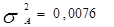Доходность облигаций характеризуется несколькими показателями. Различают купонную, текущую, и полную доходность.

Купонная доходность определена при выпуске облигаций, и нет необходимости её рассчитывать. Текущая доходность характеризует отношение поступлений по купонам к цене приобретения облигаций. Этот параметр не учитывает второй источник дохода – получение номинала и выкупной цены в конце срока. Поэтому он не пригоден при сравнении доходности разных видов облигаций. Достаточно отметить, что у облигаций с нулевым купоном ткущая доходность равна нулю. В то же время они могут быть весьма доходными, если учитывать весь срок их «жизни».

Наиболее информативным является показатель полной доходности, который учитывает оба источника дохода. Именно этот показатель пригоден для сравнения доходности инвестиций в облигации и другие ц.б. Итак, полная доходность измеряет реальную эффективность инвестиций в облигацию для инвестора в виде годовой ставки сложных процентов. Иначе говоря, начисление процентов по ставке помещения на цену приобретения облигации полностью обеспечивает выплату купонного дохода и сумму для погашения облигации в конце срока.

Облигации без обязательного погашения с периодической выплатой процентов.

Хотя подобного вида облигации встречаются крайне редко, их нужно рассматривать для получения полного представления о методике измерения полной доходности. При анализе данного вида облигаций выплату номинала в необозримом будущем во внимание не принимаем.

Текущая доходность находится следующим образом:

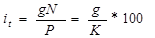где, g – объявленная норма годового дохода(купонная ставка процента);

i-текущая доходность;

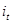 - полная доходность (ставка помещения);

Если по купонам выплата производится p раз в году (каждый раз по ставке g/p), то и в этом случае на практике применяется вышеприведённая формула, хотя суммирование доходов, выплачиваемых в разные моменты времени, строго говоря, некорректно.

Поскольку купонный доход постоянен, то текущая доходность продаваемых облигаций изменяется вместе с их изменением их рыночной цены. Для владельца облигаций, который уже инвестировал некоторые средства, эта величина постоянна.

Поскольку доход по купонам является единственным источником текущих поступлений, то очевидно, что полная доходность у рассматриваемых облигаций равна текущей в случае, когда выплаты по купонам – ежегодные: i= 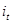. Если же проценты выплачиваются р раз в год, тогда получим:

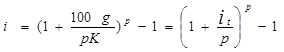Облигации без выплаты процентов.

Данный вид облигации обеспечивает её владельцу в качестве дохода разность между номиналом и ценой приобретения. Курс такой облигации всегда меньше 100. Для определения ставки помещения приравняем современную стоимость номинала цене приобретения:

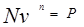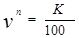       или                      где, n – срок до выкупа облигации.

После чего получим: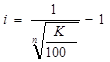

Облигации с выплатой процента и номинала в конце срока.

Проценты здесь начисляются за весь срок и выплачиваются одной суммой вместе с номиналом. Купонного дохода нет. Поэтому текущую доходность условно можно считать нулевой, поскольку соответствующие проценты получают в конце срока.

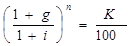
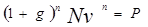Найдём полную доходность, приравняв современную стоимость дохода цене облигации:

                    или

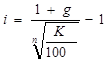Из последней формулы следует, что :

Если курс облигации меньше 100, то i>g.

Облигации с периодической выплатой процентов и погашением номинала в конце срока.

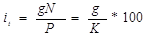Этот вид облигаций получил наибольшее распространение в современной практике. Для такой облигации можно получить все три показателя доходности – купонную, текущую и полную. Текущая доходность рассчитывается по полученной выше формуле.

Что касается полной доходности, то для её определения необходимо современную стоимость всех поступлений приравнять цене облигации. Дисконтированная величина номинала равна Nvⁿ. Поскольку поступления по купонам представляют собой постоянную ренту постнумерандо, то член такой равен gN, а современная её стоимость составит gNa_{n; i} (если купоны оплачиваются ежегодно) и gNa_{n; i} ^p, если эти выплаты производятся р раз в год. В итоге получим следующие равенства:

для облигаций с годовыми купонами

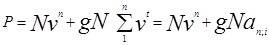Разделив на N, находим

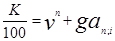Для облигаций с погашением купонов по полугодиям и поквартально получим

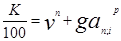где коэффициент a_{n; i} ^p - коэффициент приведения р-срочной ренты (р=2,р=4)

Во всех приведённых формулах Vⁿ означает дисконтный множитель по неизвестной годовой ставке помещения i.

Облигации с выкупной ценой, отличающейся от номинала.

В этом случае проценты начисляются на сумму номинала, а прирост капитала равен С-Р, где С – выкупная цена. Соответственно при оценке ставки помещения необходимо внести соответствующие коррективы в приведённые выше формулы:

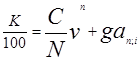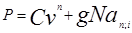Все приведённые выше формулы для расчёта полной доходности предполагают, что оценка производится на начало срока или на дату выплаты процентов. Для случаев, когда оценка производится на момент между двумя датами выплат процентов, приведённые формулы дадут смещённые оценки.

Портфельные инвестиции.

Портфельные инвестиции связаны с формированием инвестиционного портфеля и приобретением ц.б. и других активов.

Относительно небольшие денежные суммы, необходимые для приобретения финансовых активов, позволяют даже индивидуальному инвестору формировать портфель (портфель – это совокупность собранных воедино разнообразных инвестиционных ценностей или определённый набор различных ц.б. и активов). Формирование портфеля ц.б. – это комплекс операций, стратегия, умелое распределение инвестиционных сумм между набором ликвидных финансовых операций, исходя из своих возможностей.

Для коллективных инвесторов и финансовых институтов законодательство требует формирование портфеля ц.б. Владея портфелем, инвестор в большей степени заинтересован в оценке риска и доходности портфеля, чем отклонений фактических значений доходности отдельных ц.б. от ожидаемого значения. Риск и доходность отдельной ценной бумаги должны оцениваться по тому эффекту, который оказывает их включение в набор активов на риск и доходность портфеля.

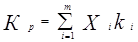Доходность портфеля (Кр) из m ц.б. есть средневзвешенная доходность по включаемым ц.б.:

Веса Xi – доля инвестирования в данную ц.б. i.

Так как рассматриваемые ц.б. рисковые, то в расчёте доходности портфеля фигурируют ожидаемые значения доходности по включенным ц.б. Ki – ожидаемая доходность ц.б. i. Полученное значение доходности портфеля также является ожидаемым значением, фактическая доходность будет отличаться от этого значения.

Например, в будущем году акции А могут обеспечить доходность не 15% (ожидаемое значение), а 30%, что увеличит фактическую доходность портфеля до 26,4% (0,6*30%+0,4*21%=26,4%). Если увеличение доходности по акциям А будет сопровождаться падением доходности акций Б, то доходность портфеля может и не отклониться от ожидаемого значения. Например, если доходность А – 30%, а доходность Б – 1.5%, то доходность портфеля не изменится: 0,6*30%+0,4*(-1,5%)=17,4

В отличие от доходности риск портфеля (как стандартное отклонение по доходности портфеля) не является средневзвешенным значением из стандартных отклонений включаемых ц.б. Стандартное отклонение портфеля может быть меньше, чем средневзвешенное значение отклонений. Теоретически возможно подобрать активы таким образом, чтобы .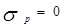

Риск портфеля из m ц.б. зависит от:

риска отдельных ц.б., включённых в него ( 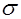i, где i – ц.б. в портфеле, i=1,2…m)

Корреляции ц.б. (синхронности изменения доходности)

доли инвестирования в каждую ц.б. Xi, Xi=Ii/I,где I – денежные средства, инвестированные в портфель; I_i – денежные средства, инвестированные в ц.б. I,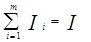

Так если по прошлым годам среднеквадратическое отклонение доходности по акциям А было 28%, а по Б – 42% и предполагается, что риск инвестирования в эти акции не изменится, то риск портфеля будет зависеть от синхронности движения цен на рассматриваемые акции и, следовательно, от реально обеспечиваемой доходности. Если цены на акции движутся синхронно (акции положительно коррелируют), то среднеквадратическое отклонение доходности портфеля (А+Б) будет равно средневзвешенному значению среднеквадратических отклонений по двум акциям: 0,6*28%+0,4*42%=33,6%. При любой другой зависимости между движением цен (и соответственно изменением доходности) на акции А и Б диверсификация капитала будет сокращать риск и среднеквадратическое отклонение по портфелю будет меньше 33,6%.

Для оценки тесноты связи используют два показателя:

1. ковариации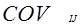

2. коэффициент корреляции (Pij)

Коэффициент корреляции более удобен для сравнения различных активов. Его значения находятся в интервале от –1 до +1.

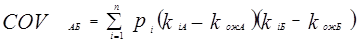
n – число возможных результатов.

Таблица №4. Пример оценки ковариации по активам А и Б.

Вероятность	Доходность по активу А	Доходность по активу Б
0,2 0,2 0,2 0,2 0,2	11% 9% 25% 7% -2% КожА=10%	-3% 15% 2% 20% 6% КожБ=8%

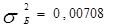
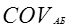=0,2*(0,11-0,1)*(-0,03-0,08)+0,2(0,09-0,1)*(0,15-0,08)+0,2*(0,25-0,1)*(0,02-0,08)+0,2*(0,07-0,1)*(0,2-0,08)+0,2*(-0,02-0,1)*(0,06-0,08)= - 0,0024.

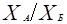
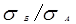Наилучший результат диверсификации достигается, если два актива (акции) отрицательно коррелируют. На практике это наблюдается крайне редко, однако для примера предположим, что Р_АБ=-1. В этом случае дисперсия портфеля равна нулю. Для такого случая портфельная стратегия в установлении весов Х_А и Х_Ббудет строиться на выполнении соотношения:             =