Рисковые активы характеризуются вероятностями значениями получения результата. Если известны все возможные значения результата (значение дохода в абсолютном выражении или относительное значение - доходность) и вероятности получения этих значений (сумма вероятностей равна 1), то такое представление называется вероятностным распределением.
Вероятностное распределение может быть представлено виде таблицы или графически. Например, если рассматривать владение недвижимостью и известны возможные цены продажи через год при различной ситуации в спросе, то вероятностное распределение может быть представлено в виде следующей таблицы №1:
Таблица №1.
| Капитал (инвестируемые средства) | Цена продажи | Вероятность (Рi), % | Отдача (доход) | Доходность (Кi), % Кi=(Цена - Инвестиции)/Инвестиции |
| 350 | 420 400 380 | 25 50 25 | 70 50 30 | 20 14,3 8,6 |
Ожидаемое значение результата определяется как сумма произведений возможных значений результата на соответствующее значение вероятности. Так ожидаемая доходность по инвестированию в недвижимость есть средневзвешенная величина возможных значений доходности: 20*0,25+ 14,3*0,5+8,6*0,25= 14,3%
Непрерывно распределение вероятности.
В данном примере предполагается, что вероятность продать актив дешевле, чем за 350 т. $ и дороже чем за 450т.$ равна нулю. Чем более заострённой будет форма кривой непрерывного распределения вероятности, тем больше вероятность, что фактическая доходность будет ближе к ожидаемому значению, и тем ниже риск принимаемого решения.
Например, инвестирование в нежилое помещение обеспечит вероятностное распределение доходности, представленное в таблице №2:
Таблица №2.
| Капитал (инвестируемые средства) | Цена продажи | Вероятность (Рi), % | Отдача (доход) | Доходность (Кi), % |
| 350 | 500 400 262,5 | 25 50 25 | 150 50 -87,5 | 42,8 14,3 -25 |
Такой вариант инвестирования более рискован, чем инвестирование в квартиру. При высоком спросе доходность может быть значительно выше (в 2 раза), однако низкий спрос приведёт к потере капитала. Непрерывное распределение вероятности по двум вариантам инвестирования представлено в Приложении на рис. №1
Первый вариант инвестирования характеризуется более заострённой формой кривой. Это означает, что фактическая доходность будет ближе к ожидаемому значению доходности 14,3%, чем по второму варианту – первый вариант менее рискован.
2.2 Нормальное распределение вероятности.
Во многих исследованиях, включающих оценку вероятности, предполагается, что вероятностное распределение является нормальным. Нормальное распределение симметрично относительно ожидаемого значения Кож. Площадь под кривой нормального распределения между любыми 2-я точками X1 и X2 является вероятностью получения результата между этими 2-я значениями.
Если Х1=10% и Х2=16%, то вероятностью получения результата в интервале (10%;16%) показана на рис..№2.
Таблица нормального распределения[3] показывает площадь под кривой, соответствующей вероятности того, что имело место z стандартных отклонений от средней. Таблица строится для нормированной величины z, которая вычисляется следующим образом: z=(Кi-Кож)/s, где Кi – наблюдаемое значение доходности. F(z)=F(-z).
Например, при z=0,7 табличное значение вероятности составит 25,8% . Попадание значений в пределах одного стандартного отклонения (z =1)происходит с вероятностью 34,13%. Это отклонение в одну сторону. Вероятность попадания в интервал (Кож-s;Кож+s) составит 68,26%, а в интервал (Кож-3s; Кож+3s) – 99,74%.
Мера риска.
Для сравнения активов и принятия решений необходима количественная оценка риска. В практике финансового менеджмента нашли отражение несколько оценок риска:
Дисперсия, как мера разброса возможных значений доходности
Стандартное отклонение. Как мера разброса, выраженная в тех же единицах, что и результат
Коэффициент вариации для ранжирования активов с различными значениями ожидаемой доходности.
Мерой разброса возможных результатов вокруг ожидаемого значения является дисперсия. Чем больше дисперсия, тем больше разброс.
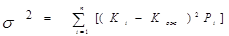 Дисперсия дискретного распределения рассчитывается по формуле:
Дисперсия дискретного распределения рассчитывается по формуле:
где n – число возможных отклонений от ожидаемого значения.
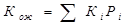 Дисперсия доходности есть сумма произведений всех возможных отклонений фактических значений доходности от ожидаемого значения на вероятность этого отклонения. Дисперсия измеряется в тех же единицах, что и результат, но возведённых в квадрат.
Дисперсия доходности есть сумма произведений всех возможных отклонений фактических значений доходности от ожидаемого значения на вероятность этого отклонения. Дисперсия измеряется в тех же единицах, что и результат, но возведённых в квадрат.
Для облегчения сравнения и анализа риска различных активов чаще используется квадратный корень из дисперсии – среднеквадратическое отклонение:
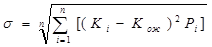
Стандартное отклонение удобнее чем дисперсия, т.к. измеряется в тех же единицах, что и результат.
Пример. Рассмотрим возможные значения общей доходности по акциям АО «Красный октябрь». Прогноз строится на возможном изменении спроса на выпускаемую продукцию и макроэкономических факторов (экономический подъём или спад. Табл. №3.1).
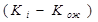 Для оценки риска через стандартное отклонение необходимо (Табл.№3.2): 1) рассчитать абсолютные отклонения возможных значений доходности
Для оценки риска через стандартное отклонение необходимо (Табл.№3.2): 1) рассчитать абсолютные отклонения возможных значений доходности
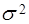 от ожидаемого значения ; 2) возвести в квадрат полученное отклонение
от ожидаемого значения ; 2) возвести в квадрат полученное отклонение 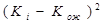 3) домножить квадраты отклонений на соответствующее значение вероятности. Сумма произведений составит значение дисперсии . Извлечём квадратный корень и получим стандартное отклонение.
3) домножить квадраты отклонений на соответствующее значение вероятности. Сумма произведений составит значение дисперсии . Извлечём квадратный корень и получим стандартное отклонение.
Таблица №3.1
| Прогноз | Доходность при рассматриваемой ситуации, % | Вероятность, % | Ожидаемая доходность, % |
| Оптимистичный Нормальный Пессимистичный | 120 70 30 | 30 40 30 | 120%*0,3+70%*0,4+30%*0,3=73 |
| Вероятность | 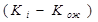
| 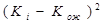
| 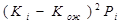
| 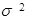
| 
|
| 0,3 0,4 0,3 | 47 -3 -43 | 2209 9 1849 | 662,7 3,6 554,7 | 1221 | 35% |
Таблица №3.2
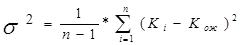 Для оценки риска по прошлым данным дисперсия рассчитывается следующим образом:
Для оценки риска по прошлым данным дисперсия рассчитывается следующим образом:
Если сравниваются активы, имеющие различную доходность, то по значению стандартного отклонения нельзя сделать вывод, какой из них является более рискованным. Для сравнения активов с различной доходностью по степени риска необходимо уравнять разброс с учётом доходности, т.е. рассчитать риск на единицу доходности, Более рискованный тот актив, по которому выше риск на единицу доходности. Таким нормированным показателем степени риска является коэффициент вариации, как отношение стандартного отклонения к ожидаемому значению результата:
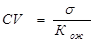
Чем выше CV, тем больше риск владения ц.б. Такое утверждение верно при равной ликвидности рассматриваемых ц.б.
Дата: 2019-12-22, просмотров: 341.