В GaAs полевая зависимость дрейфовой скорости более сложная, чем в других полупроводниках (Si, Ge), что обусловлено особенностями энергетического спктра зоны проводимости этого материала. Основной минимум зоны проводимости (долина) здесь расположен в центре зоны Бриллюэна и характеризуется высокой подвижностью (μ = 4000-8000 см2В-1с-1), а на осях ‹111› расположены долины с малой подвижностью (μ = 100 см2В-1с-1) и энергиейна 0,3 эВ выше основного минимума. В нижней долине эффективная масса m* = 0,068 m0, а в верхних долинах m* = 1,2m0. Следователь, плотность состояний в верхней долине примерно в 70 раз больше, чем в нижней. Рассмотрим малые и большие значения напряженность электрического поля.
При малых напряженностях электрического поля функция распределения электронов по энергии не меняется. В зависимости от типа полупроводника, степени совершенства и количества примеси в слабых электрических полях преобладает рассеяние на тепловых колебаниях решетки (фононах) или ионов примеси. В этом случае подвижность является постоянной величиной и дрейфовая скорость носителей пропорциональна напряженности электрического поля.
В сильных электрических полях функция распределения электронов по энергии существенно меняется. В полярных полупроводниках, таких как GaAs, определяющую роль начинает играть неупругое рассеяние на оптических фононах. Это приводит к насыщению дрейфовой скорости носителей и уменьшению подвижности с ростом напряженности электрического поля.
Получим соотношение между дрейфовой скоростью и напряженностью электрического поля, опираясь на предположение о равенстве электронных температур верхней и нижней долинах Te. Величина энергетического зазора между минимумами зоны проводимости ∆E = 0,31 эВ для GaAs. Введем обозначения: m*1 и m*2 – эффективные массы, μ1 и μ2 – подвижности, n1 и n2 – концентрации электронов в нижней и верхней долинах, причем полная концентрация носителей заряда равна n = n1 + n2. Плотность стационарного тока в полупроводнике можно представить следующим образом:
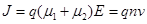
| (3.1) |
где v – средняя дрейфовая скорость
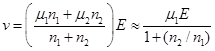
| (3.2) |
так как μ1 >> μ2. Отношение заселенностей верхней и нижних долин, разделенных энергетическим зазором ∆E, равно:
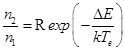
| (3.3) |
где R – отношение плотностей состояний и
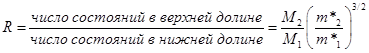
| (3.4) |
M1 и M2 – число верхних и нижних долин соответственно. Для GaAs M1 = 1, а число верхних долин равно 8, но они расположены у края зоны Бриллюэна, и поэтому M2 = 4. Используя значение эффективных масс электронов в GaAs m*1 = 0,067m0, m*2 = 0,55 m0, получим R=94.
Поскольку электрическое поле ускоряет электроны и увеличивает их кинетическую энергию, электронная температура Te превышает температуру решетки T. Электронная температура определяется с помощью времени релаксации энергии:
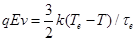
| (3.5) |
где время релаксации энергии τe предполагается равным 10-12с. Подставив v из выражения (3.30) и n2/n1 из выражения (3.31) в последнюю формулу, получим
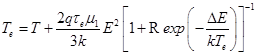
| (3.6) |
Используя это равенство, можно рассчитать зависимость Te от напряженности электрического поля при заданной величине T. Из выражений (3.2) и (3.3) следует соотношение между дрейфовой скоростью и полем:
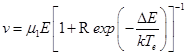
| (3.7) |
Рассчитанные с помощью этих выражений типичные зависимости v от E для GaAs при трех температурах решетки приведены на рисунке.
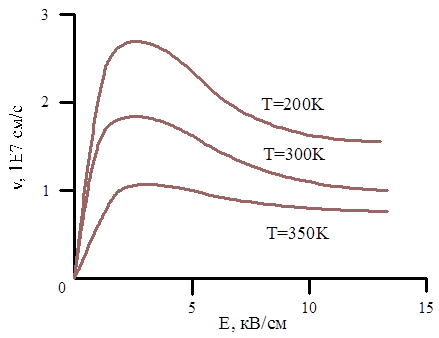
Рис.8 Зависимости дрейфовой скорости от напряженности электрического поля для GaAs при трех температурах решетки.
ВАХ в линейной области
Математическое описание ВАХ AlGaAs/InGaAs/GaAs псевдоморфного транзистора с высокой подвижностью электронов (pHEMT). Для описания модели ВАХ сделаны следующие предположения для AlGaAs/InGaAs/GaAs pHEMT:
· постепенное приближение канала;
· как только происходит насыщение скорости около стока в конце канала, ток стока начинает увеличиваться только благодаря модуляции длины канала;
· двухкусочная аппроксимация используется, чтобы представить отношение между скоростью и электрическим полем.
ВАХ AlGaAs/InGaAs/GaAs pHEMT получена для случая, когда сопротивление источника и сопротивление стока предполагают равным нолю. Кривая ВАХ имеет две области: линейную область (VDS <VDSAT) и область насыщенности (VDS> VDSAT).
Рассмотрим линейную область. Ток стока в линейной области записывается:
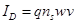
| (3.8) |
где q – заряд электрона, ns=2D электронный газ, w - длина канала и v – скорость электрона. Скорость, с которой 2DEG электроны перемещаются в канале InGaAs, определяется электрическим полем в канале и подвижностью электронов. Однако если электрическое поле превышает некоторое критическое значение - Ec, в этом случае скорость достигает насыщения. Зависимость v(E) можно представить следующим образом:
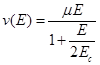 для для 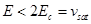 , для , для 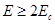
| (3.9) |
где E - продольная составляющая электрического поля, μ – подвижность электронов, 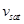 - скорость насыщения и
- скорость насыщения и 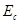 - критическое значение электрического поля.
- критическое значение электрического поля.
Вторая особенность при описании ВАХ HEMT транзистора заключается в зависимости концентрации носителей в канале HEMT в неравновесных условиях при приложении напряжения к затвору.
Из уравнения Пуассона для p-типа:
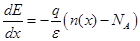
| (3.10) |
при интегрировании от области истощения E=0 до E следует, что
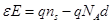
| (3.11) |
где d – толщина узкозонного полупроводника GaAs и E(d)=0. При достаточно малых d и NA, получаем связь электрического поля и концентрации носителей:
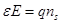
| (3.12) |
Исходя из физических соображений и согласно рисунку:
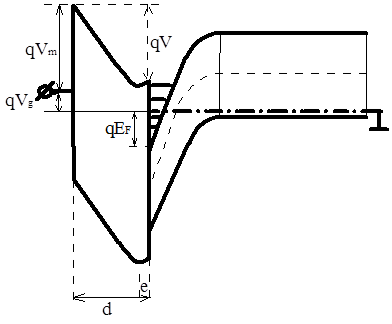
Рис.9 AlGaAs/GaAs гетеростуктура.
мы можем записать зависимость концентрации носителей в канале HEMT при приложении напряжения к затвору в виде:
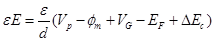
| (3.13) |
так как 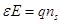 , то отсюда следует:
, то отсюда следует:
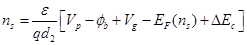
| (3.14) |
или
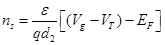
| (3.15) |
здесь Ef – это уровень Ферми относительно дна зоны проводимости в канале и является функцией концентрации носителей на поверхности ns в канале, d2 – это полная толщина слоя AlGaAs, ∆Ec – неоднородность зоны проводимости в гетероструктуре и φb – высота барьера (затвора) Шоттки.
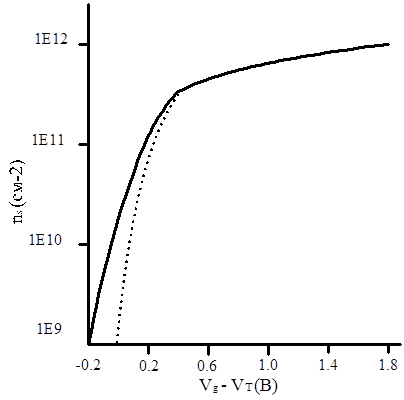
Рис.10 Зависимость концентрации носителей заряда от приложенного напряжения на затвор при температуре 300К: прямая – точное значение, а точечная кривая – Das Gupta.
Для моделирования ВАХ по модели Das Gupta предлагается записать зависимость Ef псевдоморфного транзистора AlGaAs/InGaAs/GaAs (pHEMT) от ns в виде полинома:
| EF=K1+K2ns1/2+K3ns, | (3.16) |
значение Ef рассчитано для трех значений ns, а именно 2 × 1010, 2 × 1011 и 2 × 1012 /см. После замены значений Ef в выражении, стоящем выше, и решения системы из трех уравнений, можно оценить значения коэффициентов К1, К2, К3. Тогда в системе AlGaAs/GaAs, ns запишется как:
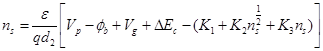
| (3.17) |
Преобразуя это выражение, мы получим квадратичное уравнение относительно ns1/2 :
| K4ns+K2ns1/2−(Vg−VT−K1)=0, | (3.18) |
где 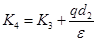 . Решение данного уравнения может быть записано в виде:
. Решение данного уравнения может быть записано в виде:
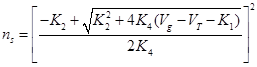
| (3.19) |
Оно обеспечивает отношение для ns в 2-хмерном газе (2-DEG) как функцию напряжения на затворе. В случае напряжения канала V(x) из-за присутствия Vd (напряжения на стоке) выражение для ns запишется:
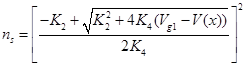
| (3.20) |
где Vg1=Vg−VT−K1.
Подставляя уравнение (3.8) в (3.9), ток стока в линейной области выражается:
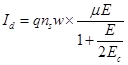
| (3.21) |
Заменяя E = dV / dx в уравнении (3.32) и преобразуя, мы получаем:
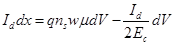
| (3.22) |
Интегрируя это уравнение от источника (x=0, V=0) до стока (x=L, V=Vd), мы получаем:
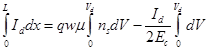
| (3.23) |
ток стока Id может бить записан как:
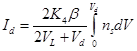
| (3.24) |
где 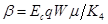 и
и 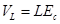 .
.
Подставляя величину ns из уравнения (3.20) в уравнение выше (3.24) и преобразуя, получаем:
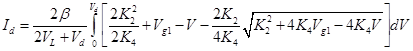
| (3.25) |
После интегрирования:
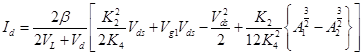
| (3.26) |
где 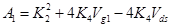 и
и 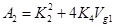 .
.
ВАХ в области насыщения
Дата: 2019-12-22, просмотров: 397.