Для решения дифференциального уравнения (2.6) необходимо определить граничные условия для волновой функции ξ(z). Для этого необходимо сшить на границе значения функции в виде стоячей волны в потенциальной яме и в виде затухающей экспоненты в барьере, а также ее производной. Ис­пользуя аналогию потенциальной ямы в ОПЗ с прямоугольной потенциаль­ной ямой и приводя соответствующие выкладки, имеем для величины на­чальной фазы ∆ _I стоячей волны в ОПЗ:

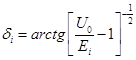                                                 .                            (2.10)

Значение типа sin (∆_i) будет соответствовать значению волновой функции на границе, в то время как максимальное значение волновой функции sin (ξ(z)) будет порядка единицы. В реальных условиях величина потенциального барьера U₀ на границе полупроводник-диэлектрик, например Si-SiO₂, порядка U₀ ~ 3 эВ, в то время как величины Е _i составляют сотые доли электронвольта Е _i < 0,05 эВ. Таким образом, как следует из приведенных оценок, значение волновой функции ξ(z) на границе полупроводника составляет десятые или сотые доли максимального значения волновой функции, достигаемого на не­котором расстоянии z. Этот факт позволяет полагать величину волновой функции равной нулю, ξ(z) = 0, при z = 0. Отметим, что этот момент является исключительно важным, поскольку соответствует нулевой вероятности на­хождения электрона на границе ОПЗ. Следовательно, квантовое рассмотре­ние уже в силу постановки граничных условий на волновую функцию требу­ет нулевой плотности n(z) на поверхности полупроводника, в то время как классическое рассмотрение дает здесь максимальное значение. Аналогично, при 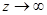 величина .

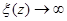Таким образом, для решения (2.6) требуются граничные условия:

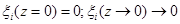                                                                        (2.11)
и необходимо выполнение условия нормировки:

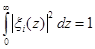                                                                                  (2.10)                                                 

Предположим, что мы решили уравнение (2.6) и знаем величины энер­гии 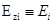 и соответствующие волновые функции ξ_i(z). Тогда полное число электронов N_i в i-той квантовой подзоне на единицу площади будет:

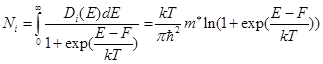                                           (2.13)

При наличии нескольких минимумов энергии Е( k ) в двумерной подзоне Бриллюэна на поверхности значения E_i и ξ_i(z) будут еще иметь метку, соот­ветствующую выбранному минимуму J .

Распределение электронов по толщине канала будет в этом случае опре­деляться степенью заполнения подзон поперечного квантования и видом функции в каждой подзоне:

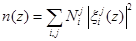                                                                                       (2.14)

Полное число носителей в канале Г_п на единицу площади будет:

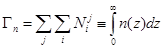                                                                                 (2.15)

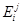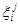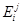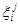Таким образом, основная задача при квантовомеханическом рассмотре­нии электрона в потенциальной яме состоит в решении уравнения (2.6) и нахождении спектра энергий  и вида волновых функций . Оказывается, что в аналитическом виде выражение  и  можно получить только в случае треугольной потенциальной ямы, которая реализуется в об­ласти слабой инверсии и в квантовом пределе, когда заполнена только одна квантовая подзона.