Известно, среднее расстояние, на котором локализо­ваны свободные носители в ОПЗ от поверхности полупроводника, невелико и составляет величину λ_с = (20*200)А. Оценим величину дебройлевской дли­ны волны λ электрона в кристалле. Считая энергию электрона тепловой, ве­личину эффективной массы равной массе свободного электрона т₀, имеем для величины λ:

                                                         λ = h[2m₀kT]                                                (2.1)

Подставляя в (2.1) значения постоянных величин, получаем при ком­натной температуре величину длины дебройлевской волны λ~ 200 А. Как следует из приведенных оценок, в инверсионных слоях и слоях обогащения длина дебройлевской волны электрона становится сравнима с его областью локализации в потенциальной яме вблизи поверхности. Очевидно, что при этом становится существенным учет квантовомеханического характера дви­жения свободных носителей в ОПЗ.

Стационарное состояние, описывающее состояние электрона в ОПЗ в одноэлектронном приближении, будет определяться из решения уравнения Шредингера:

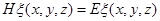                                     (2.2)

где ξ(х, у, z ) - волновая функция, описывающая движение электрона, Е -энергия электрона.

Решение (2.2) будем искать, используя метод эффективных масс. Отме­тим, что при применении метода эффективных масс требуется, чтобы потен­циал внешнего поля ψ(z) менялся значительно слабее потенциала поля кри­сталлической решетки. В ОПЗ, в случае сильного обогащения или инверсии, это условие, вообще говоря, может не выполняться.

Оператор Гамильтона Н для ОПЗ с использованием метода эффективных масс будет:

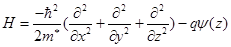                                                                (2.3)

Движение электрона в потенциальной яме ОПЗ локализовано только в направлении, перпендикулярном поверхности, вдоль же поверхности, в на­правлении х и у, электрон движется как свободный с эффективной массой m *. Будем также считать величину эффективной массы скалярной величиной. В этом случае волновую функцию электрона ξ(х, у, z ) можно представить в виде суперпозиции волновой функции для электрона, двигающегося свободно параллельно поверхности:

,

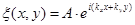и волновой функции для дви­жения перпендикулярно поверхности ξ(z):

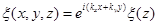                                                                                 (2.4)

Решение уравнения (2.2) с учетом выражения для Н в виде (4.3) и ξ(х,у, z ) в виде (2.4) приводит к следующему выражению для энергии элек­трона в ОПЗ:

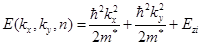                                  ,                          (2.5)

где Е _zi имеет смысл энергии электрона для движения перпендикулярно по­верхности и описывается уравнением:

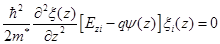                                                                   (2.6)

Решение (2.6) дает квантованный, т.е. дискретный, спектр значений энергии Е _zi (i=0, 1, 2...). Величина Е _zi вид волновых функций ξ_i(z)опреде­ляются, как следует из (2.6), величиной и законом изменения потенциала ψ(z) т.е. глубиной и формой потенциальной ямы.

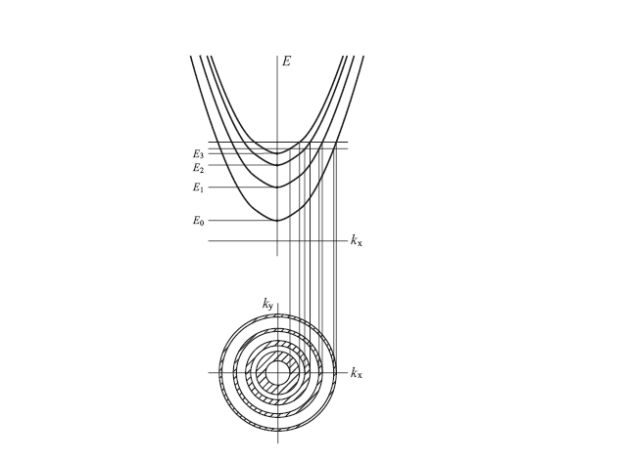
Рис.6 Зависимость энергии E от волнового числа k для двумерного электронного газа. Расстояние между подзонами ∆E соответствует расстоянию между квантовыми уровнями в одномерной потенциальной яме.

Из (2.5) и (2.4) следует, что при каждом значении i= 0, 1, 2... элек­тронный газ в ОПЗ двумерен, т.е. полностью описывается волновыми числа­ми k_x , k_y и обладает согласно (2.5) квазинепрерывным спектром энергии. Область энергий, которыми в соответствии с (2.5) может обладать электрон при данном квантовом числе i = 0, 1, 2..., называется поверхностной подзо­ ной. Поверхностные подзоны представляют собой параболоиды вращения, отстоящие друг от друга по оси энергий на расстояние 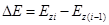. На рисунке 2. 1 приведена зонная диаграмма таких поверхностных подзон.