Исследовательской частью данного курсового проекта является адаптивное регулирование скорости двигателя по моменту инерции механизма.
Для осуществления автоматического управления объектами, параметры которых меняются и для получения хорошей динамики, используем систему адаптивного управления. Существует два типа адаптации : параметрическая адаптация и сигнальная адаптация. Наиболее простым для синтеза является способ сигнальной адаптации.
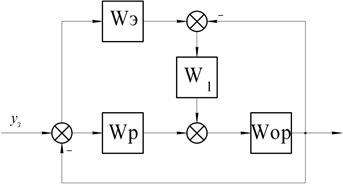
Рис.15
На рисунке 8.1 изображена система с сигнальной адаптацией, здесь
Wэ – эталонная модель электропривода.
Wр – передаточная функция регулятора.
Wop – передаточная функция объекта регулирования.
Определяем параметры, необходимые для моделирования адаптивного регулятора скорости по моменту инерции.
При моделировании используем двигатель постоянного тока 2ПБ132LГУХЛ4, используемый в данном курсовом проекте, со следующими параметрами:
- номинальная мощность: 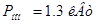 ;
;
- номинальная скорость вращения вала: 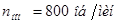 ;
;
- номинальное напряжение питания: 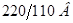 ;
;
- номинальный ток якоря: 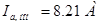 ;
;
- суммарный момент инерции: 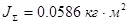 .
.
По номинальным данным двигателя рассчитаем следующие величины:
Номинальный момент: 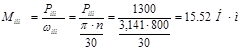 ;
;
Постоянная двигателя: 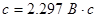 .
.
Сопротивление цепи якоря: 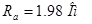 .
.
Индуктивность цепи якоря: 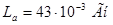 .
.
Угловая скорость холостого хода: 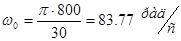 .
.
Коэффициент передачи тиристорного преобразователя:
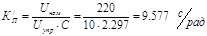
Определяем электромеханическую и механическую постоянные времени:
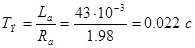
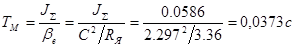
Определяем естественную жёсткость механической характеристики:
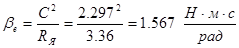
Коэффициент обратной связи по скорости:
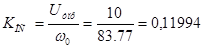
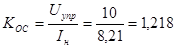
Для расчета адаптивного регулятора скорости двигателя по моменту инерции двигателя произведём расчет системы адаптивного управления подчинённого регулирования без учёта момента инерции двигателя, т.е. примем 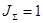 .
.
* Контур момента *:
Контур момента системы подчинённого регулирования настраиваем на технический оптимум:
Передаточная функция объекта регулирования:
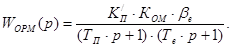
Желаемая функция условно разомкнутой системы:
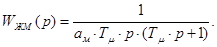
Передаточная функция регулятора:
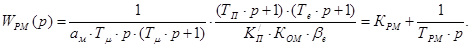
где 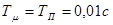 ;
;
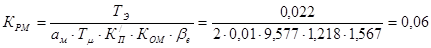 ;
;
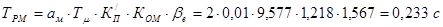 .
.
* Контур скорости *:
Контур скорости системы подчинённого регулирования настраиваем на технический оптимум:
Передаточная функция объекта регулирования:
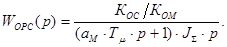
Желаемая функция условно разомкнутой системы:
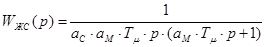 .
.
Передаточная функция регулятора:
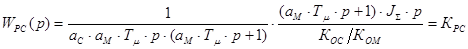 ,
,
где 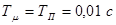 ;
;
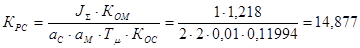
Составляем модель на языке структурных схем в среде MаtLab:
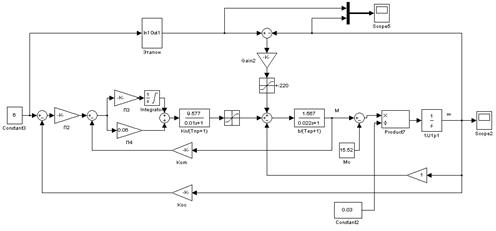
Рис.16.Программа на языке структурных схем в среде MatLab
При моделировании использованы следующие параметры:
− Напряжение управление Uy = 6B, что соответветствует напряжению питанию Uп = 132 В.
− двигатель нагружен номинальным моментом,равным 15.52 Н·м.
− Моделирование произведем при трех значениях момента инерции: J1 = 0.03 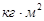 , J2 = 0.0586
, J2 = 0.0586 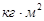 (номинальный момент инерции ), J3 =0.15
(номинальный момент инерции ), J3 =0.15 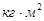
Дата: 2019-12-22, просмотров: 364.