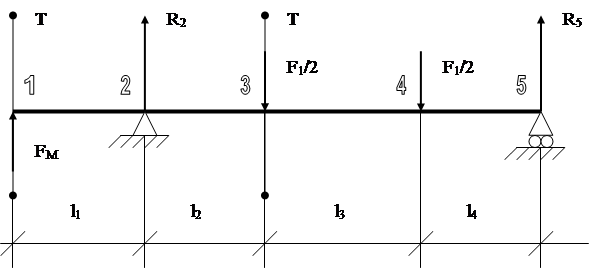
Расчетная схема вала
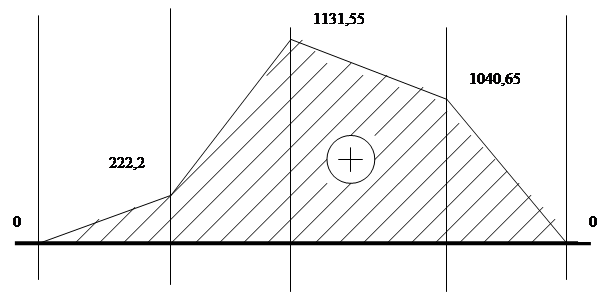
Эпюра изгибающих моментов Мизг, кН мм
 |
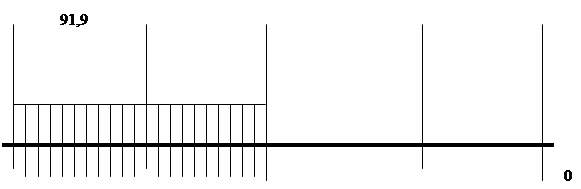Эпюра крутящих моментов Ткр, кН мм
Исходные данные: l1 = 100 мм; l2 = l4 = 325 мм; l3 = 450 мм;
Т – крутящий момент на валу, Т = Т4 = 817,7 кН мм.
R2 и R5 – силы реакции опоры в соответствующих точках.
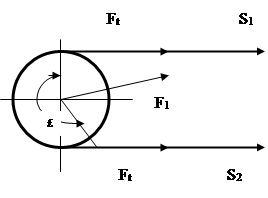
F1 – сила, действующая на вал в следствии натяжения ветвей конвейера, кН; Эта сила определяется из следующего условия:
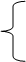F1 = S1 + S2, (28)
Ft = S1 – S2.
где: Ft – окружное усилие на рабочем элементе ИМ (см. исходные данные на курсовой проект);
S1 и S2 – силы натяжения ветвей конвейера, кН; которые определяются из следующего соотношения:
S1/ S2 = ef £ (29)
где: e – основание логарифма;
f – коэффициент трения между лентой и барабаном; для данного случая принимается равным f = 0,3;
£ - угол обхвата, рад. (см. исходные данные на курсовой проект).
Значит сила натяжения первой ветви конвейера S1 будет:
S1 = ef £ * S2 (30)
Тогда, используя второе уравнение нашей системы (28), найдем силу натяжения второй ветви S2:
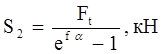(31)
Следовательно:
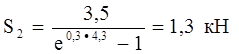
Значит, сила натяжения первой ветви:
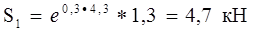
Отсюда, сила, действующая на вал в следствии натяжения ветвей конвейера, будет:
F1 = 4,7 + 1,3 = 6,0 кН
Fм – сила муфты, которая определяется по формуле:
Fм = Kм * Ftм, кН (32)
где: Kм – коэффициент, учитывающий тип муфты; так как в нашем случае муфта цепная, то принимаем Kм = 0,2;
Ftм – сила внутри муфты, определяется по следующей формуле:
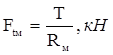(33)
где: Rм – радиус муфты, который в данном случае будет определятся по формуле:
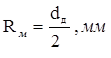(34)
Тогда, радиус муфты будет:
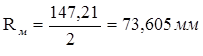
Отсюда сила внутри муфты будет:
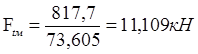
Следовательно, сила муфты:
Fм = 0,2 * 11,109 = 2,222 кН
Для того чтобы проверить вал на статическую прочность, необходимо рассчитать вал на изгиб с кручением. Определим для начала реакции в опорах вала R2 и R5.
Составляем уравнения равновесия вала:
 |
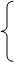Σ F = 0; Fм + R2 – F1/2 – F1/2+ R5 = 0; (35)
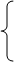Σ M(*)2 = 0. -Fм * l1 – F1 * l2/2 – F1 * (l2 + l3)/2 + R5 * (l2 + l3 + l4) = 0.
Тогда:
 |
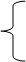R2 = F1 – Fм – R5; (36)
R5 = (Fм * l1 +( F1 (2 l2 + l3))/2)/( l2 + l3 + l4).
Отсюда: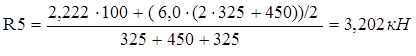 
Тогда: R2 = 6,0 – 2,222 – 3,202 = 0,576 кН
Определяем моменты в различных точках приводного вала:
М(.)1 = 0 кН мм;
М(.)2 = Fм * l1 = 2,222 * 100 = 222,2 кН мм;
М(.)3 = Fм * (l1 + l2) + R2 * l2 = 2,222 (100 + 325) + 0,576 * 325 = 1131,55 кН мм;
М(.)4 = Fм * (l1 + l2 + l3) + R2 * (l2 + l3) – F1 * l3/2 = 2,222 (100 + 325 + 450) + + 0,576 (325 + 450) – 6,0 * 450/2 = 1944,25 + 446,4 – 1350 = 1040,65 кН мм;
М(.)5 = Fм * (l1 + l2 + l3 + l4) + R2 * (l2 + l3 + l4) – (F1 * (l3 + l4))/2 – F1 * l4 = = 2,222 (100 +2 * 325 + 450) + 0,576 (2 * 325 + 450) – (6,0 (325 + 2 * 450))/2 =2666,4 + 633,6 – 3675 = 0.
При расчете вала на статическую прочность, он рассчитывается на совместное действие изгиба и кручения. Прочность характеризуется внутренними механическими напряжениями в деталях.
Прочность – способность сопротивляться разрушению при действии заданных нагрузок.
Внутренние силы (межатомные, межмолекулярные), действующие на единичной площадке, называются внутренними механическими напряжениями. Они появляются при действии внешних сил. Они бывают нормальные и касательные.
σ = √ σизг2 + 4 τкр2 ≤ [σ] (37)
где: σизг – действующее нормальное напряжение кручения;
τкр – касательное напряжение кручения.
Действующее нормальное напряжение кручения определяется по формуле:
(38)
где: Мизг – изгибающий момент, действующий в сечении вала, кН мм2 (см. эпюру изгибающих моментов);
Wx – осевой момент сопротивления сечения вала, мм3.
Осевой момент сопротивления сечения вала равен:
Wx = 0,1 d3, мм3 (39)
где: d – диаметр вала в данном сечении, мм (см. п.2.1.5)
Касательное напряжение кручения определяется по формуле:
(40)
где: Ткр – крутящий момент, кН мм (см. эпюру крутящих моментов);
Wр – полярный момент сопротивления сечения вала, мм3.
Полярный момент сопротивления сечения вала равен:
Wр = 0,2 d3, мм3 (41)
Тогда: σ = √ (Мизг/0,1 d3)2+ 4(Tкр/ 0,2d3)2 ≤ [σ] (42)
Допустимые значения напряжений для стали марки Ст 45 при одновре-менном действии изгиба и кручения равны 80 МПА.
Проверку производим в точках 2 и 3:
σ(.)2 =√ (222,2/0,1 * 653)2 + 4(91,9/0,2 * 653)2 = 8,7 МПа
σ(.)3 =√ (1131,55/0,1 * 853)2 =18,4 МПа
Условие прочности выполняется
Дата: 2019-12-22, просмотров: 232.
