Законы Кеплера.

Движение планет Солнечной системы по их орбитам вокруг Солнца удовлетворяет трем законам Кеплера. Эти законы можно получить из закона всемирного тяготения Ньютона, рассматривая в первом приближении Солнце и планеты как материальные точки.

1. Все планеты Солнечной системы движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

2. Радиус-вектор, проведенный от Солнца к планете, за одинаковые промежутки времени прочерчивает одинаковые площади.

3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей эллиптических орбит этих планет

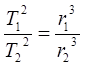
Закон всемирного тяготения И. Ньютона.

Сила всемирного тяготения F прямо пропорциональна произведению масс m₁ и m₂ тел и обратно пропорциональна квадрату расстояния г между телами:

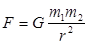
- (справедлив для точечных масс, для однородных шаров и однородных шаровых слоев)

Гравитационная постоянная, её физический смысл и опытное определение.

G-гравитационная постоянная. Определена Кавендишем в 1797г. с помощью крутильных весов. Гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек единичной массы, находящихся на единичном расстоянии одна от другой.

Кавендиш измерил разницу между углами закручивания :

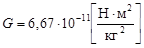
Гравитационное поле.

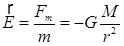
Гравитационное взаимодействие между тепами осуществляется посредством создаваемого гравитационного поля, называемого также полем тяготения. Силовой характеристикой поля служит его напряженность: (вблизи поверхности Земли напряженность поля тяготения равна ускорению свободного падения) Энергетической характеристикой поля является потенциал:

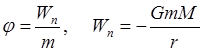
(потенциальная энергия поля тяготения называется взятая с обратным знаком работа по перемещению тела на бесконечность).

Законы сохранения в нерелятивистской механике, их связь со свойствами симметрии пространства и времени. Законы сохранения энергии, импульса и момента импульса. Примеры их проявления

В механике сформулированы законы сохранения: закон сохранения импульса, закон сохранения энергии, закон сохранения момента импульса. Для некоторых систем их можно получить из законов Ньютона.

1) Закон сохранения импульса

p = mυ

p=∑mυ=const

Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (он подчиняется законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импульса – фундаментальный закон природы.

Закон сохранения импульса является следствием определенного свойства симметрии пространства – его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются; иными словами, не зависят от выбора положения начала координат ИСО.

Отметим, что импульс сохраняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю.

Второй закон Ньютона F=dp/dt. В замкнутой системе F=0, dp=0, p=const.

Импульс системы = произведению массы системы на скорость ее центра масс p=mV_c.

Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неизменным.

Примеры проявления закона сохранения импульса:

Отдача при стрельбе 0 = m₁υ₁+Mυ₂

Реактивное движение (ракета движется в безвоздушном пространстве).

Абсолютно упругий удар

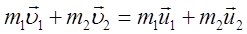
Абсолютно неупругий удар

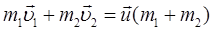
Закон сохранения импульса для механических систем используется и действует при всех известных взаимодействиях, т. к. импульсом обладает и поле.