Пространство и время в нерелятивистской физике. Система отсчета. Кинематика материальной точки. Прямолинейное равномерное и равноускоренное движение. Криволинейное движение

Стр 1 из 17Следующая ⇒

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Движение происходит в пространстве.

Механическое движение – это изменение положения тела в пространстве с течением времени относительно других тел.

Понятие пространства определяет протяженность предметов и их взаимное расположение.

Описание:

Пространство описывается двумя способами:

1. Эвклидово ΕΔ=180°

2. Не эвклидово E≠180°

Свойства пространства:

1. Однородность (безразличие к переносам)

2. Изотропность (безразличие к поворотам)

3. непрерывность

4. трехмерность

Изменение времени происходит с помощью периодических процессов.

Свойства времени:

1. Непрерывность

2. Однонаправленность

3. Одномерность

4. Изотропность

Система отсчета: тело отсчета, система координат, вектор, часы

Кинематика материальной точки

Материальная точка – тело, размерами и формой которого можно пренебречь в данных условиях движения.

Кинематика изучает только движение тел без внимания на причины его возникновения.

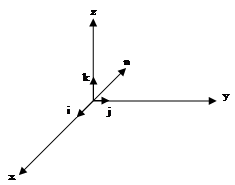
Декартова система координат

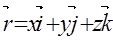
Кинематические уравнения движения:

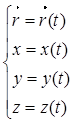
Указать траекторию – задать путь, пройденный матер. точкой по траектории.

Траектория – это линия, вдоль которой движется тело.

Путь – длина траектории

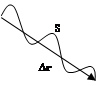
S – длина траектории

Δr – перемещение за время Δt

Перемещение – вектор, соединяющий нач. и конечную точки траектории.

Скорость точки – первая производная перемещения по времени

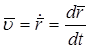
Направление вдоль траектории

Ускорение –быстрота изменения скорости (это вторая производная перемещения по времени)

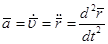
Ускорение раскладывается на нормальное и тангенциальное:

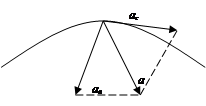
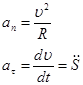
Частные виды движения

I. Прямолинейное

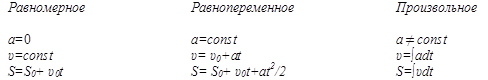
Равномерное движение по окружности

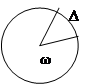
Δφ – угловое перемещение

ω – угловая скорость

ω=dφ / dt

υ=[ ω, r]

ω определяется по правилу буравчика

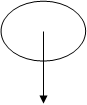
Угловое ускорение

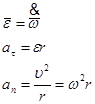
2. Принцип относительности Галилея. Преобразования Галилея. Законы Ньютона и границы их применимости. Принцип суперпозиции сил

ИСО – это система отсчета, относительно которой все тела, не взаимодействующие с другими телами, движутся прямолинейно и равномерно.

Принцип относительности Галилея: законы динамики одинаковы для всех ИСО.

Преобразования Галилея: для координат и времени.

При переходе из одной С. О. в другую.

u – скорость K’ относительно K

r = r ’+ ut

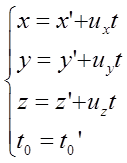
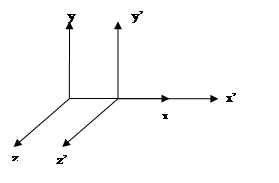
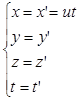
Если преобразования Галилея продифференцировать по времени, то получается закон сложения скоростей:

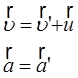
Законы Ньютона

I Закон Ньютона: существуют такие С. О., относительно которых тело покоится или движется равномерно и прямолинейно, если на него не действуют другие тела или действие других тел скомпенсировано

II Закон Ньютона: ускорение, полученное телом, прямо пропорционально равнодействующей сил, приложенных к телу и обратно пропорционально массе тела.

III Закон Ньютона: сила действия = силе противодействия.

F₁₂= -F₂₁

Границы применимости законов Ньютона:

Законы Ньютона выполнимы при движении со скоростями v<<c

Законы Ньютона не выполняются в НИСО

Силы инерции

Рис. 1 – шар движется с ускорением a =- ω . Шар ведет себя так, как если бы на него действовала некоторая сила:

I = ma = - mω

Рис. 2 – на шар действует деформированная пружина с силой F = -kx. Она же сообщает шару ускорение относительно вагона.

Дело обстоит так, как если бы на шар действовала некая сила: I = ma =- mω , которая уравновешивала бы силу F.

Особенности сил инерции

Силы инерции вызваны ускоренным движением самой СО, поэтому к силам инерции не применим второй закон Ньютона

Силы инерции действуют на тело только в НИСО.

Для любой системы тел, находящейся в НИСО, силы инерции являются внешними силами, следовательно, нет замкнутых систем, и поэтому не выполняются законы сохранения.

I~m. Поэтому в поле сил инерции, как и в поле сил тяготения, все тела движутся с одним и тем же ускорением.

Пространство в НИСО неоднородно, неизотропно.

Время в НИСО: неоднородно, ∑Δ≠180°

Гравитационное поле.

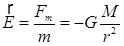
Гравитационное взаимодействие между тепами осуществляется посредством создаваемого гравитационного поля, называемого также полем тяготения. Силовой характеристикой поля служит его напряженность: (вблизи поверхности Земли напряженность поля тяготения равна ускорению свободного падения) Энергетической характеристикой поля является потенциал:

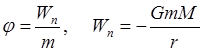
(потенциальная энергия поля тяготения называется взятая с обратным знаком работа по перемещению тела на бесконечность).

Законы сохранения в нерелятивистской механике, их связь со свойствами симметрии пространства и времени. Законы сохранения энергии, импульса и момента импульса. Примеры их проявления

В механике сформулированы законы сохранения: закон сохранения импульса, закон сохранения энергии, закон сохранения момента импульса. Для некоторых систем их можно получить из законов Ньютона.

1) Закон сохранения импульса

p = mυ

p=∑mυ=const

Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (он подчиняется законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импульса – фундаментальный закон природы.

Закон сохранения импульса является следствием определенного свойства симметрии пространства – его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются; иными словами, не зависят от выбора положения начала координат ИСО.

Отметим, что импульс сохраняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю.

Второй закон Ньютона F=dp/dt. В замкнутой системе F=0, dp=0, p=const.

Импульс системы = произведению массы системы на скорость ее центра масс p=mV_c.

Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неизменным.

Примеры проявления закона сохранения импульса:

Отдача при стрельбе 0 = m₁υ₁+Mυ₂

Реактивное движение (ракета движется в безвоздушном пространстве).

Абсолютно упругий удар

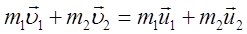
Абсолютно неупругий удар

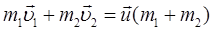
Закон сохранения импульса для механических систем используется и действует при всех известных взаимодействиях, т. к. импульсом обладает и поле.

Гармонические колебании

x = Asin ( ω ₀ t + φ ₀ )

ω ₀ – циклическая частота – число полных колебаний, которые совершаются за 2П единиц времени φ=2πν

T=2π/ω – период колебаний

Вынужденные механические колебания – колебания, возникающие под действием внешней периодически изменяющейся силы

x = Acos ( ω ₀ t + φ ₁ )

В пружине

F = F ₀ cos ωt

Резонанс: явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы

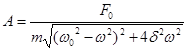
δ – коэффициент затухания

Образование и спектр энергетических зон в кристалле

Спектр возможных значений энергии валентных электронов распадается на ряд чередующихся разрешенных и запрещенных зон. Физическая причина этого в том, что электроны в кристалле движутся не свободно, а в периодическом электрическом поле кристаллической решетки. Запрещенная энергетическая зона соответствует значениям энергии, которыми не могут обладать электроны в кристалле. Каждая из разрешенных зон состоит из близко расположенных дискретных уровней энергии, число которых равно N – количеству атомов в кристалле. Так как энергетическое расстояние между отдельными уровнями в зоне около 10^–23 эВ, то разрешенная зона характеризуется квазинепрерывным спектром энергии.

Внешние (валентные) электроны взаимодействуют сильнее, поэтому перекрытие волновых функций, а следовательно и расщепление уровней для них больше. Соответственно, заметно расщепляются лишь уровни энергии, занимаемые этими электронами, как и более высоко лежащие свободные (не занятые электронами) уровни: электроны перестают быть локализованными вблизи своих атомов, они перемещаются по всему кристаллу – образуется система электронов проводимости.

Состояния внутренних атомных электронов столь мало перекрываются в кристалле, что образуется локализованных электронов, и можно считать ядро вместе со всеми внутренними электронами единым целым – ионом, или атомным остовом. В зонной теории твердое тело рассматривается как совокупность ионов и электронов проводимости.

Закон Кулона (в 1785)

Он гласит, что сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними.

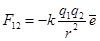
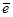- единичный векторный орт, имеющий поправку от q₁, на который действует сила F₁₂

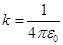
ε₀=8,85 · 10^-12 Ф/м

Опыт Милликена

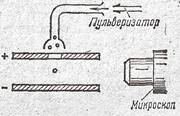
Заряд электрона был определен с большой точностью Милликеном в 1909 г. В закрытое пространство между горизонтально расположенными пластинами конденсатора (рис) Милликен вводил мельчайшие капельки масла. При разбрызгивании капельки электризовались, и их можно было устанавливать неподвижно, подбирая величину и знак напряжения на конденсаторе. Равновесие наступало при условии

P’=e’E (1)

Здесь e’ – заряд капельки, P’ – результирующая силы тяжести и архимедовой силы, равная

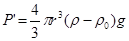(2)

ρ – плотность капельки, r – ее радиус, ρ₀ – плотность воздуха).

Из формул (1) и (2), зная r, можно было найти e. Для определения радиуса измерялась скорость равномерного падения капельки в отсутствие поля. Равномерное движение капельки устанавливается при условии, что сила P’ уравновешивается силой сопротивления 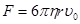(η – вязкость воздуха):

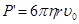(3)

Движение капельки наблюдалось с помощью микроскопа. Для измерения υ₀определялось время, за которое капелька проходила расстояние между двумя нитями, видимыми в поле зрения микроскопа.

Точно зафиксировать равновесие капельки очень трудно. Поэтому вместо поля, отвечающего условию (1), включалось такое поле, под действием которого капелька начинала двигаться с небольшой скоростью вверх. Установившаяся скорость подъема υ_Е определяется из условия, что сила P’ и сила 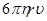в сумме уравновешивают силу e’E:

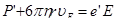(4)

Исключив из уравнения (2), (3) и (4) P’ и r, получим выражение для e’:

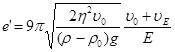
(в эту формулу Милликен вносил поправку, учитывающую, что размеры капелек были сравнимы с длиной свободного пробега молекул воздуха).

Итак, измерив скорость свободного падения капельки υ₀ и скорость ее подъема υ_Е в известном электрическом поле Е, можно было найти заряд капельки e’. Произведя измерение скорости υ_Е при некотором значении заряда e’, Милликен вызывал ионизацию воздуха, облучая пространство между пластинами рентгеновскими лучами. Отдельные ионы, прилипая к капельке, изменяли ее заряд, в результате чего скорость υ_Е также менялась. После измерения нового значения скорости снова облучалось пространство между пластинами и т. д.

Измеренные Милликеном изменения заряда капельки Δe’ и сам заряд e’ каждый раз получались целыми кратными одной и той же величины e. Тем самым, была экспериментально доказана дискретность электрического заряда, т. е. тот факт, что всякий заряд слагается из элементарных зарядов одинаковой величины.

Значение элементарного заряда, установленное с учетом измерений Милликена и данных, полученных другими методами, равно

e = 1,6 · 10^-19 Кл

Опыт Томсона

Удельный заряд электрона (отношение e/m) был впервые измерен Томсоном в 1897 г. с помощью разрядной трубки, изображенной на рисунке. Выходящий из отверстия в аноде А электронный пучок проходил между пластинами плоского конденсатора и попадал на флуоресцирующий экран, создавая на нем светящееся пятно. Подавая напряжение на пластины конденсатора, можно было воздействовать на пучок практически однородным электрическим полем. Трубка помещалась между полюсами электромагнита, с помощью которого можно было создавать на том же участке пути электронов перпендикулярное к электрическому однородное магнитное поле (пунктирная окружность на рисунке). При выключенных полях пучок попадал на экран в точке О. Каждое из полей в отдельности вызывало смещение пучка в вертикальном направлении.

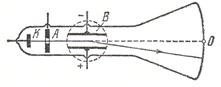
Включив магнитное поле и измерив вызванное им смещение следа пучка,

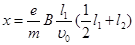(1)

Томсон включал также электрическое поле и подбирал его значение так, чтобы пучок снова попадал в точку О. В этом случае электрическое и магнитное поля действовали на электроны пучка одновременно с одинаковыми по величине, но противоположно направленными силами. При этом выполнялось условие

eE= eυ₀B (2)

Решая совместно уравнения (1) и (2), Томсон вычислил e/m и υ₀.

Серия Брэкета

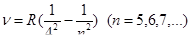
Пфунда

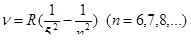
Хэмфри

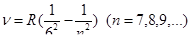
Все приведенные выше серии в спектре атома водорода могут быть описаны одной формулой, называемой формулой Бальмера:

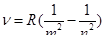
Где m имеет в каждой данной серии постоянное значение, m =1, 2, 3, 4, 5, 6 (определяет серию), n принимает целочисленные значения, начиная с m +1 (определяет отдельные линии этой серии). Спектр атома водорода правильно описывается на основе постулатов Бора.

Первый постулат Бора: из бесконечного множества электронных орбит, возможных с точки зрения классической механики, в действительности осуществляются лишь некоторые дискретные орбиты, удовлетворяющие определенным квантовым условиям. Электрон, находящийся на одной из таких орбит, несмотря на то, что он движется с ускорением, не излучает электромагнитных волн.

Второй постулат Бора: излучение испускается или поглощается в виде светового кванта hω. При переходе электрона с одной дискретной орбиты на другую (из одного стационарного состояния в другое) величина кванта равна разности энрергий тех стационарных состояний, между которыми осуществляется квантовый скачок электрона:

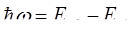
Набор возможных дискретных частот, квантовых переходов и определяет линейчатый спектр водорода.

Спектральный анализ

Исследование линейчатого спектра вещества позволяет определить, из каких веществ он состоит и в каком количестве содержится каждый элемент. Количественное содержание элемента в исследуемом образце определяется путем сравнения интенсивности отдельных линий спектра этого элемента с интенсивностью линий другого химического элемента, количественное содержание которого известно. Спектральный анализ широко применяется при поисках полезных ископаемых для определения химического состава образцов руды. В промышленности спектральный анализ позволяет контролировать состав сплавов и примесей, вводимых в металл.

Достоинства: высокая чувствительность и быстрота получения результатов. Спектральный анализ позволяет определить химический состав небесных тел, удаленных от Земли на расстоянии в миллиарды световых лет, для этого используют спектры поглощения (по этим спектрам определяют температуру звезд, состав, и по смещению – скорость движения).

25. Опыты Резерфорда, планетарная модель строения атома Резерфорда – Бора. Составные элементы атомного ядра. Ядерные силы

В развитии представлений о строении атома велико значение опытов английского физика Э. Резерфорда (1871 — 1937) по рассеянию альфа-частиц в веществе. Альфа-частицы возникают при радиоактивных превращениях; они являются положительно заряженными частицами с зарядом 2е и массой, примерно в 7300 раз большей массы электрона. Пучки альфа-частиц обладают высокой монохроматичностью (для данного превращения имеют практически одну ж ту же скорость (порядка 10⁷м/с)).

Резерфорд, исследуя прохождение альфа-частиц в веществе (через золотую фольгу толщиной примерно 1 мкм), показал, что основная их часть испытывает незначительные отклонения, но некоторые альфа-частицы (примерно одна из 20 000) резко отклоняются от первоначального направления (углы отклонения достигали даже 180°). Так как электроны не могут существенно изменить движение столь тяжелых и быстрых частиц, как альфа-частицы, то Резерфордом был сделан вывод, что значительное отклонение альфа-частиц обусловлено их взаимодействием с положительным зарядом большой массы. Однако значительное отклонение испытывают лишь немногие альфа-частипы; следовательно, лишь некоторые из них проходят вблизи данного положительного заряда. Это, в свою очередь, означает, что положительный заряд атома сосредоточив в объеме, очень малом по сравнению с объемом атома.

На основании своих исследований Резерфорд в 1911 г. предложил ядерную (планетарную) модель атома. Согласно этой модели, вокруг положительного ядра, имеющего заряд Zе ( Z— порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер 10^-15 — 10^{-14 м и массу, практически равную массе атома, в области с линейными размерами порядка 10-10} м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Z электронов.

Для простоты предположим, что электрон движется вокруг ядра по круговой орбите радиуса r. При этом кулоновская сила взаимодействия между ядром и электроном сообщает электрону центростремительное ускорение. Второй закон Ньютона для электрона, движущегося по окружности под действием кулоновской силы, имеет вид

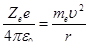(1)

где m и υ — масса и скорость электрона на орбите радиуса r, ε₀ — электрическая постоянная.

Уравнение (1) содержит два неизвестных: r и υ. Следовательно, существует бесчисленное множество значений радиуса и соответствующих ему значений скорости (а значит, и энергии), удовлетворяющих этому уравнению. Поэтому величины г, υ (следовательно, и Е) могут меняться непрерывно, т. е. может испускаться любая, а не вполне определенная порция энергии. Тогда спектры атомов должны быть сплошными. В действительности же опыт показывает, что атомы имеют линейчатый спектр. Из выражения (1) следует, что при r≈10^{-10 м скорость движения электронов}υ≈10⁶ м/с, а ускорение υ²2/r = 10²² м1001ммм/с². Согласно электродинамике, ускоренно движущиеся электроны должны излучать электромагнитные волны и вследствие этого непрерывно терять энергию. В результате электроны будут приближаться к ядру и в конце концов упадут на него. Таким образом, атом Резерфорда оказывается неустойчивой системой, что опять-таки противоречит действительности.

Попытки построить модель атома в рамках классической физики не привели к успеху: модель Томсона была опровергнута опытами Резерфорда, ядерная же модель оказалась неустойчивой электродинамически и противоречила опытным данным.

Преодоление возникших трудностей потребовало создания качественно новой — квантовой — теории атома.

Ядерные силы.

Между составляющими ядро нуклонами действуют особые, специфические для ядра силы, значительно превышающие кулоновские силы отталкивания между протонами. Они называются ядерными силами.

С помощью экспериментальных данных (рассеяние нуклонов на ядрах, ядерные превращения и т. д.) доказано, что ядерные силы намного превышают гравитационные, электрические и магнитные взаимодействия и не сводятся к ним. Ядерные силы относятся к классу так называемых сильных взаимодействий.

Перечислим основные свойства ядерных сил,

1) ядерные силы являются силами притяжения;

2) ядерные силы являются короткодействующими — их действие проявляется только на расстояниях примерно 10^-15м. При увеличении расстояния между нуклонами ядерные силы быстро уменьшаются до нуля, а при расстояниях, меньших их радиуса действия, оказываются примерно в 100 раз больше кулоновских сил, действующих между протонами на том же расстоянии;

3) ядерным силам свойственна зарядовая независимость: ядерные силы, действующие между двумя протонами, или двумя нейтронами, иди, наконец, между протоном и нейтроном, одинаковы по величине.

Отсюда следует, что ядерные силы имеют неэлектрическую природу;

4) ядерным силам свойственно насыщение, т. е. каждый нуклон в ядре взаимодействует только с ограниченным числом ближайших к нему нуклонов. Насыщение проявляется в том, что удельная энергия связи нуклонов в ядре (если не учитывать легкие ядра) при увеличении числа нуклонов не растет, а остается приблизительно постоянной;

5) ядерные силы зависят от взаимной ориентации спинов взаимодействующих нуклонов. Например, протон и нейтрон образуют дейтрон (ядро изотопа (Н)) только при условии параллельной ориентации их спинов;

6) ядерные силы не являются центральными, т. е. действующими по линии, соединяющей центры взаимодействующих нуклонов.