Установим связь между потенциалом 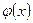, напряженностью электрического поля E(х) в ОПЗ и плотность объемного заряда ρ(х) в полупроводнике.

Примем потенциал в глубине полупроводника за нуль. Значение потенциала на границе раздела диэлектрик – полупроводник (х=0) обозначим через 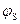. Величина  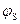называется поверхностным потенциалом.

При изгибе зон вниз поверхность полупроводника n–типа проводимости обогащается основными носителями. Этому режиму согласно выражению (1) соответствует потенциал 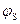>0. Изгибу зон вверх соответствует потенциал 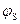<0.

Величина и знак поверхностного потенциала 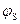 однозначно определяют соотношения между концентрациями основных и неосновных носителей на поверхности полупроводника n_S и p_S.

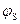>0 – режим обогащения (n_S>n₀, n_S»p_S);

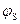=0 – режим плоских зон (n_S=n₀, p_S=p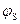₀);

<0, 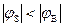 - режим обеднения (n_S<n₀, n_S»p_S);

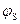<0, 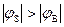 - режим инверсии (p_S»n_S, n₀»n_S).

Связь потенциала 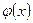 с плотностью объемного заряда ρ(х) определяется уравнением Пуассона, которое для одномерного случая записывается в виде

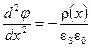,                                                        (11)

где 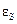 - диэлектрическая проницаемость полупроводника, 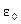=8,86·10^-12 Ф/м – диэлектрическая постоянная.

В общем случае

ρ(х)= e(N_D– N_A+ p– n),                                    (12)

где N_D и N_A – концентрации ионизированных доноров и акцепторов. В глубине полупроводника (за пределами ОПЗ) объемный заряд равен нулю. Отсюда

N_D– N_A= n₀– p₀.

Используя выражения (9) и (10), получим

n–p=n₀exp(βφ)–p₀ exp(-βφ).

Уравнение Пуассона принимает вид:

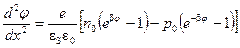.                                        (13)

Интегрируя уравнения (13), находим

,

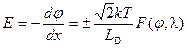где

;

;

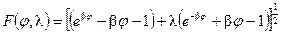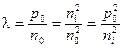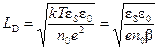.                                           (14)

Величина L_D - длина экранирования Дебая.

Напряженность электрического поля в полупроводнике положительна при 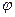>0 (зоны изогнуты вниз) и отрицательна при 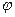<0 (зоны изогнуты вверх). На границе с диэлектриком напряженность электрического поля E_S равна

E_S= .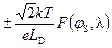

Плотность пространственного заряда Q_SC в приповерхностной области полупроводника по теореме Гаусса связана с напряженностью электрического поля соотношением

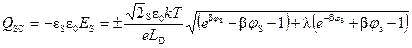.        (15)

Рассчитанная по формуле (15) зависимость модуля плотности пространственного заряда Q_SC от поверхностного потенциала 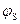 для кремния n – типа представлена на рис.10.

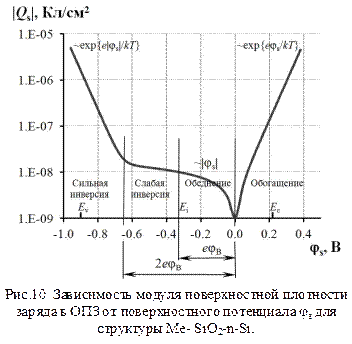При положительных значениях  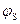(обогащение) заряд Q_SC отрицателен. Учитывая, что уже при 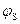, равном нескольким φ_T (при комнатной температуре  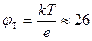мВ) экспоненциальный член в выражении (15) значительно больше остальных, то заряд Q_SC можно представить в виде

.

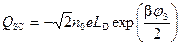При 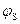=0 зоны плоские и Q_SC=0. Пр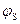и <0 и 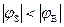 (обеднение) заряд в ОПЗ обусловлен главным образом положительными ионами доноров:

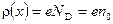
Решение уравнения Пуассона в этом случае имеет вид

,

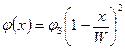где

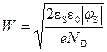                                                          (16)

- толщина области обеднения.

Можно убедиться, что связь между 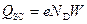 и j_S определяется выражением

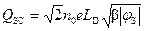.                                               (17)

При достаточно больших отрицательных значениях ( 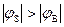) осуществляется режим инверсии. В области слабой инверсии  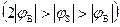зависимость заряда Q_SC  от поверхностного потенциала по-прежнему выражается функцией (8). Сильная инверсия наступает при поверхностном j_S, равном

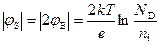.                                           (18)

Это условие соответствует равенству поверхностной концентрации p_S неосновных носителей (дырок) и концентрации основных носителей (электронов) 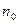 в объеме полупроводника.

В режиме сильной инверсии 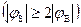 выражение для заряда Q_SC приобретает вид

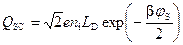.                                      (19)

Изменение Q_SC с увеличением φ_S согласно выражению (19) происходит лишь за счет изменения концентрации неосновных носителей в инверсном слое 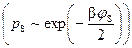, заряд  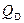и толщина обедненного слоя W остаются неизменными. Максимальное значение ширины ОПЗ найдем, воспользовавшись формулами (16) и (18):

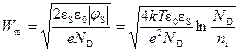.                       (20)