Предварительный расчет валов состоит в определении диаметров из условия изгибной прочности.
Определяем крутящий момент на 1-ом ведущем валу:
T1=9550·P/n1=9550·5,5/965=54,43 Н·м;
Уровень прочности при расчете вала на кручение имеет вид: T=T/Wp<=[T];
Принимаем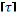 
=20МПа.
Wp=0,2·d13;
Откуда
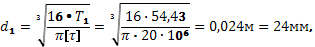
из конструктивных соображений d1=24 мм.
Определяем предварительно по крутящему моменту диаметр 2-го вала ступени редуктора;
T2=T1·U12· 
=54,43·7,5·0,98·0,995=398Н·м;
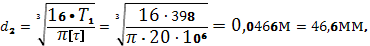
Принимаем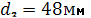 
Проверочный расчёт быстроходного вала
Для расчета вала необходимо составить его расчетную схему. Вал представим как балку на двух опорах: шарнирно-подвижной и шарнирно-неподвижной. После этого необходимо:
- разметить точки, в которых расположены условные опоры;
- определить величину и направление действующих на вал сил: окружной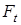 
, радиальной 
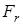. В планетарной передаче эти силы взаимокомпенсируются. Поскольку на валы не действуют осевые силы, то 
.
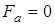- построить эпюры изгибающих и крутящих моментов.
Разбиваем вал на участки.
L1 = 65мм, L2 = 62мм, L3 = 68мм.
Силы действующие в зацеплении:
- сила от муфты Fm.
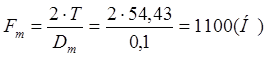, где Dm – диаметр муфты.
Найдём моменты действующие на вал и построим эпюру моментов.
.
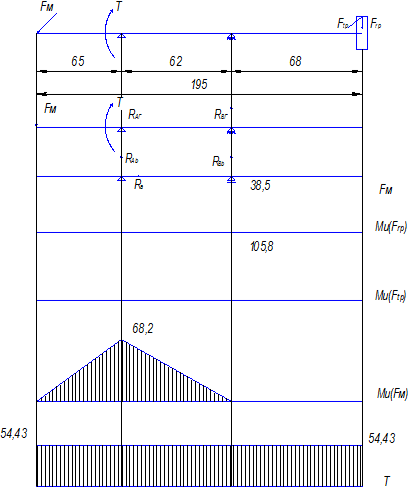
Рис. 2 – Эпюра изгибающих моментов
Определим суммарные изгибающие моменты (рис. 2):
- изгибающий момент в вертикальной плоскости:
;
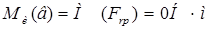- изгибающий момент в горизонтальной плоскости:
;
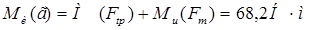- суммарный изгибающий момент в опасном сечении вала:
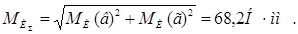
Расчёт на статическую прочность
Данный расчёт производят в целях предупреждения остаточных пластических деформаций в том случае, если вал работает работает с большими перегрузками (кратковременными).
При этом кратковременные напряжения определяют по формуле:
,
.
.
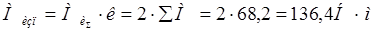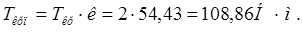
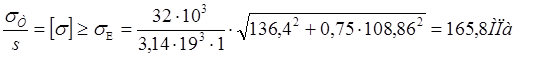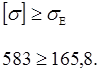
Расчёт на выносливость
Данный расчёт проводят в форме проверки коэффициента запаса прочности по усталости. Коэффициент запаса при одновременном действии нормальных и касательных напряжений
,
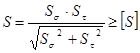где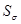 
– коэффициент запаса для нормальных напряжений;
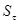– коэффициент запаса для касательных напряжений.
.
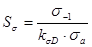Здесь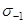 
= 250 МПа – предел выносливости гладкого образца при симметричном цикле напряжений изгиба;
, 
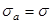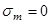– для изменения напряжений изгиба по симметричному знакопеременному циклу;
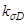– эффективный коэффициент концентрации напряжений для детали.
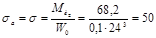МПа.
,
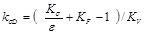где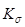 
= 1,8 – эффективный коэффициент концентрации напряжений для полированного образца;
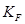= 1,25 – коэффициент состояния поверхности;
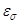= 0,86 – коэффициент влияния абсолютных размеров детали;
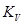= 1,5 – коэффициент влияния упрочнения.
= 1,47.
Коэффициент запаса
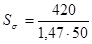= 5,7.
Коэффициент запаса для касательных напряжений
.
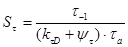Здесь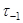 
= 210 МПа – предел выносливости гладкого образца при симметричном цикле напряжений кручения;
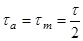– для нереверсивной передачи при изменении напряжений кручения по пульсирующему отнулевому циклу;
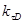– эффективный коэффициент концентрации напряжений для детали;
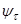= 0,05 – коэффициент чувствительности материала к асимметрии цикла напряжений при кручении.
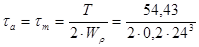= 9,8 МПа.
,
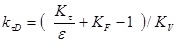где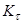 
= 1,45 – эффективный коэффициент концентрации напряжений для полированного образца;
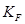= 1,25 – коэффициент состояния поверхности;
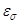= 0,86 – коэффициент влияния абсолютных размеров детали;
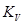= 1,5 – коэффициент влияния упрочнения.
= 1,29.
Коэффициент запаса
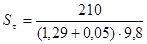= 16.
Коэффициент запаса при одновременном действии нормальных и касательных напряжений
.
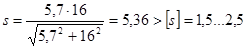Дата: 2019-12-10, просмотров: 219.
