Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Метод Ньютона може бути віднесено до оптимізаційних задач в наступній постановці

 

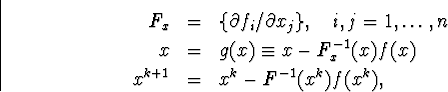         (2.2.1)

 

тобто потрібно вирішити систему F_x(x^k+1-x^k)=-f(x^k) . Будемо використовувати 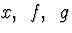- розуміючи під цим вектора.

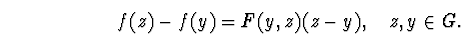
Теорема 3. Якщо f_i(x) безперервні, разом з першими похідними в опуклій області G , що містить рішення систем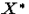и і при матриця F_x не вироджена, то існує така околиця 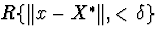що при кожнім 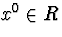метод Ньютона сходиться к.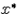

 

Доказ. Розглянемо

 

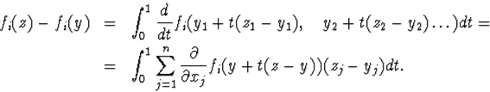(2.2.2)

 

Введемо

 

 

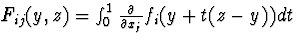
і матрицю

 

.

 

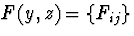Очевидно, що F(x,x)= F(x) , тобто маємо тотожності

 

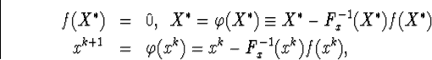(2.2.3)

тоді

 

 

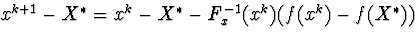
Використовуючи одержимо

 

 

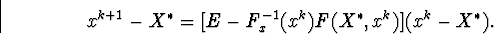
Поблизу околиці 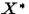для кожного 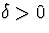найдеться таке x⁰ , що якщо

 

,

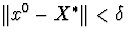то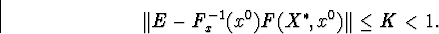

Тоді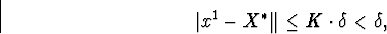

тобто

 

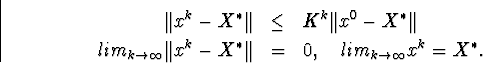
На початкове наближення x⁰ накладена умова, яку перевірити складно.

 

Теорема Канторовича 4. Якщо функції f_i(x) безперервні разом зі своїми 1 -ми і 2 -ми похідними в деякій опуклій області G , що містить крапку x⁰ разом з її околицею 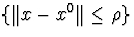і виконані наступні умови:

1) у крапці x⁰ існує матриця F^-1 така

2) 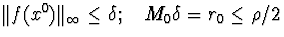                        (2.2.4)

3) 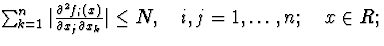         (2.2.5)

4) 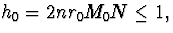   (2.2.6)

 

те послідовність x^k+1=x^k-f^-1_x(x^k)F(x^k) сходиться к. 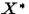 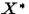є єдиним рішенням системи f(x)=0 в області 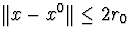і має місце оцінка

 

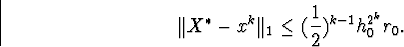
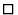
Доведемо 3 нерівності

 

а)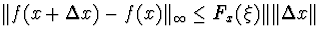

б)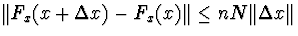

в)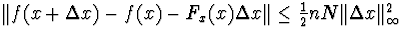

а)

б)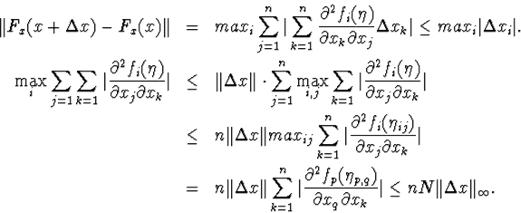

в)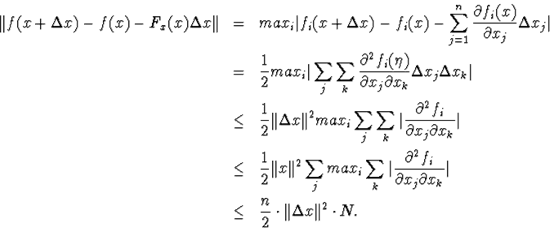

 

З ітераційного процесу при k=0

 

 

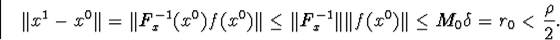
Тепер

 

 

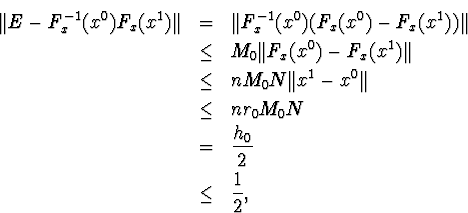
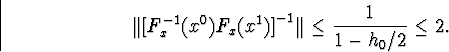
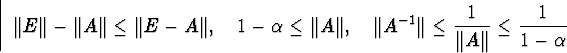
тобто матриця F^-1_x(x⁰)F_x(x¹) не вироджена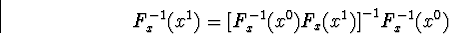, і

 

і

З F_x(x⁰)(x¹-x⁰)+f(x⁰)=0

 

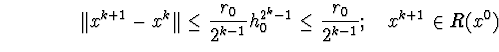
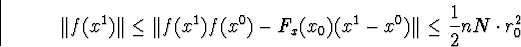
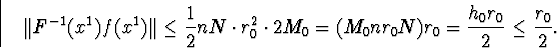
Покажемо, що при всіх k мають місце нерівності:

 

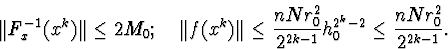(2.2.6)

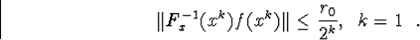
Нехай має місце m=k-1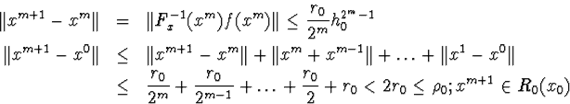

 

Повторимо нерівності

 

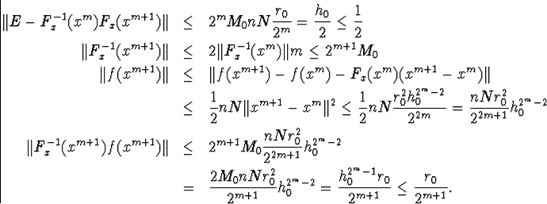
Нерівність показує, що в колі R послідовність x^k є фундаментальною, тобто мається межа.

Оцінимо збіжність

 

 

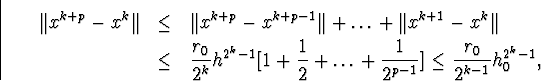
тобто, спрямовуючи 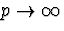права частина не міняється, 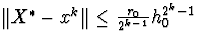, тобто при 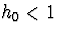дуже гарна збіжність.

Модифікація методу Ньютона в тім, що F^-1_x(x^kp) обчислюють не на кожнім кроці; при 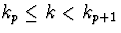матриця не міняється, що різко зменшує число арифметичних дій, але накладає більш тверді обмеження на область і швидкість збіжності.

 

Методика розрахунку точності прогнозування за критерієм Персона

 

Для визначення точності прогнозування необхідно знайти різницю між прогнозованим і реальним значенням параметра.

Нуль-гіпотеза приймається, якщо критерій узгодження Пірсона (або «хі-квадрат»)

 

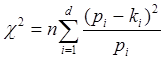,                           (2.3.1)

 

буде менший або дорівнювати табличному значенню цього критерію при достатньо великому значенні довірчої ймовірності. Фрагмент таблиці критерію Пірсона χ2(r, р) поданий нижче. Тут п – розмір вибірки, k_і – прогнозоване значення параметру; р_і – реальне значення параметру: d – загальна кількість діапазонів, на які розбита область існування випадкової величини. r= d - 1 – число ступенів свободи.

Таблиця 2.3.1. Значення χ2(r, р)

r р	1	3	5	7	10	15	20	25	30
0,99	0	0,115	0,554	1,239	2,56	5,23	8,26	11,52	14,95
0,95	0,004	0,352	1,145	2,17	3,94	7,26	10,85	14,61	18,49
0,9	0,016	0,584	1,61	2,83	4,86	8,55	12,44	16,47	20,6
0,8	0,064	1,005	2,34	3,82	6,18	10,31	14,58	18,94	23,4