Економічні цикли, сезонність продаж, цикл життя товару або послуги та інші чинники можуть суттєво впливати на економічні показники окремого підприємства. Періодичність економічних процесів викликана зміною життєвої активності людей протягом доби, тижня, місяця та року (існують і більші періоди циклічності).
Тому перед дослідниками постає задача підбору такого виду функції, яка б своєю формою відповідала основним формам періодичних і неперіодичних залежностей економічних процесів. Другою задачею є визначення коефіцієнтів обраної функції за вибіркою статистичних даних.
Існуючі в економіці залежності повинні мати не тільки періодичні функції, але й експоненціальні та степеневі. Тому була обрана наступна формула
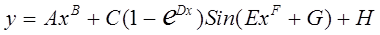 , (2.1.1)
, (2.1.1)
де х – аргумент, у – функція, A - Н – константи, e – основа натурального логарифму. В залежності від чисельних значень констант, ця формула дає множину кривих, представлену на рис.2.1.1.
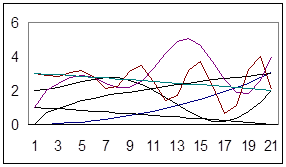
Рис. 2.1.1 Типи кривих, які можна створити за допомогою формули (2.1.1)
Вирішення другої задачі ускладнюється тим, що не існує таких математичних перетворень, які б дозволили лінеаризувати (2.1.1), щоб потім отримати значення констант A - Н методом регресії або найменших квадратів. Тому був застосований наступний оптимізаційний підхід:
1. Встановити довільні значення констант A - Н .
2. Для всіх значень аргументу і довільних значень констант розрахувати величину у, яку позначимо як ур за формулою.
3. Для кожного значення функції знайти (ур – уф)2, де уф – фактичне значення функції, отримане за статистичними даними.
4. Вирішити оптимальну задачу з функціоналом виду
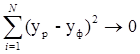 , (2.1.2)
, (2.1.2)
а параметрами, що змінюються, будуть константи A - Н . Де N – розмір статистичної вибірки.
Вже перші розрахунки за допомогою функції “Пошук рішень” електрон-них таблиць Excel показали, що константи E та G визначаються як нулі у випадку, коли амплітуда синусоїди менше середнього значення функції у 3-10 разів. Тому, для збільшення точності розрахунку, рекомендується встановлювати обмеження на значення констант за наступним правилом:
1. На графіку, який було побудовано за статистичними даними, виділяється елемент кривої, що нагадує синусоїду і знаходиться проміжок значень аргументу, на якому ця синусоїда здійснює повне коливання – Δх. Тоді, для константи E треба встановити наступне обмеження
E ≤ (0,5 – 1,5) 2π/Δх1. (2.1.3)
2. Початкові значення констант B та F рекомендується становити рівними одиниці, константи Н – середньому арифметичному статистичного значення функції, константу – D - 0.05, А=0.
3. Константа C визначається з максимальної амплітуди Δу тієї частини графіку, яка визначена як синусоїдальна, і має наступні обмеження
С ≤ (0,4 – 0,6) Δу. (2.1.4)
Наведемо приклади застосування запропонованої методики. Нижче під заголовками наведені графіки різних періодичних процесів економіка, а в таблиці 2.1.1. подані значення констант для цих графіків, знайдені з урахуванням. В малюнках прийняті наступні умовні позначення ур – ■ уф – ♦.
Таблиця 2.1.1.
| Номер рисунка | Значення констант для (1) | |||||||
| A | B | C | D | E | F | G | H | |
| 2 | 0,00145 | 7,34660 | 150000 | -29,39 | 0,9 | -0,436 | -0,39 | 98923 |
| 3 | 11042,3 | -3,901 | 25396,8 | -0,899 | 0,855 | 0,8772 | 0,409 | 226049 |
| 4 | -22,22 | 0,7731 | 4204,4 | -0,009 | 0,0006 | 4,5492 | 7,829 | 285,39 |
| 5 | 595,51 | -4,862 | 60 | 0,0235 | 1 | 0,8697 | 9,5 | 45 |
| 6 | 17,0537 | 0,57627 | 19,9770 | -0,05 | 201,32 | -94,12 | 1,684 | 30,100 |
Споживання палива енергогенеруючою компанією
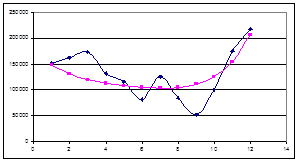
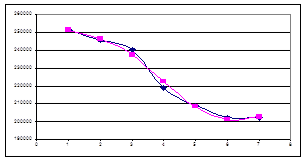
Рис. 2.1.2. За місяцями Рис. 2.1.3. За днями тижня
Потік замовлень на підприємство зв’язку
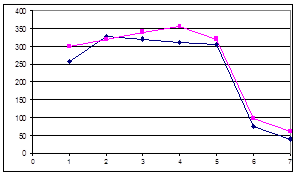
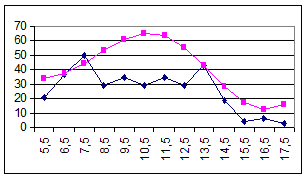
Рис. 2.1.4. За днями тижня Рис. 2.1.5. За годинами робочого дня
Залежність прибутку приватного підприємства від свого попереднього значення.
В цьому випадку була використана так звана авторегресійна модель, тобто залежність прибутків та збитків (прибутків зі знаком мінус) від своїх попередніх значень. Оскільки формула не дає бажаного результату, якщо якесь число зі статистичної вибірки має від’ємне значення (константи B та F можуть бути дробовими, а, отже, жодне значення аргументу не може бути від’ємним, бо воно знаходиться через логарифмування), то до значень статистичної вибірки було додано число більше за найбільше за модулем від’ємне значення аргументу.
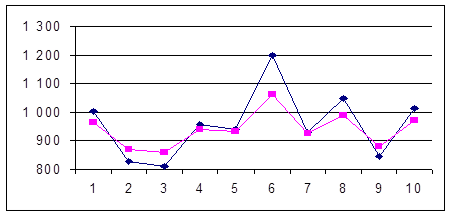
Рис.2.1.6 Прибуток за кварталами
З отриманих результатів проведених досліджень можна зробити наступні висновки:
1. Запропонований оптимізаційний алгоритм дозволяє будувати модель циклічних економічних процесів за будь-якою наперед обраною формулою.
2. Запропонована формула дозволяє будувати моделі різних за своєю природою економічних процесів.
Дата: 2019-12-10, просмотров: 416.