Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 Обоснование необходимости проведения моделирована выбранного техпроцесса (место и роль моделирования в обще схеме организации контроля качества данной ТО)

Таблица 1

Номер опыта

х0

х1

х2

х3

х1х2

х1х3

х2х3

х1х2х3

у1

y2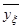

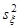
1 2 3 4 5 6 7 8

+ + + + + + + +

– + – + – + – +

– – + + – – + +

– – – – + + + +

+ – – + + – – +

+ – + – – + – +

+ + – – – – + +

– + + – + – – +

85 35 88 92 73 41 54 71

93 26 90 77 82 26 46 70

89 30,5 89 84,5 77,5 33,5 50 70,5

32 40,5 2 112,5 40,5 112,5 32 0,5

91 28,5 88,38 85,12 75,48 35,5 50,62 69,88

 

Современный ТП характеризуется повышенной сложностью и наличием множества контролируемых и неконтролируемых фак­торов, влияющих на него.

Для описания систем, представленных в виде «черного ящика», успешно применяется полиномиальная модель, даю­щая возможность учитывать множество входных факторов. Зави­симость выхода технологического процесса (вектора отклика Y) в этой модели от вход­ных факторов х_i , х _j и т. д. определяется формулой

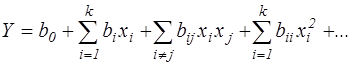
. Построение математической модели методом ПФЭ

Полиномиальная модель технологического процесса для трех входных факторов опре­деляется из уравнения

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₂x₁x₂ + b₁₃x₁x₃ + b₂₃x₂x₃+b₁₂₃x₁x₂x₃ .

Здесь х _i = (x_i – х _0i)/ D .x _i – безразмерная величина; х _0i – центр пла­на; D .x _i – интервал варьирования по i-му фактору.

Матрица планирования типа ПФЭ (2³) представлена табл. 1.

Здесь у º Е_проб, В; 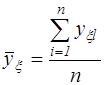 – средние значения результатов

параллельных опытов; x =1, ..., N; N = 8; п = 2. По данным табли­цы проводим следующие вычисления:

1) определяем дисперсию среднего арифметического внутри выборки

.

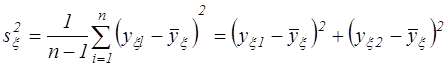2) осуществляем проверку однородности дисперсий по крите­рию Кохрена

                                ,

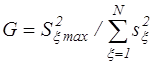Критическое значение критерия Кохрена:

,

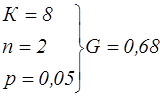G < G_T, поэтому гипотеза о равенстве выборочных дисперск верна (с определенной степенью риска р=0,05), т. е. экспериметы воспроизводимы.

3) рассчитываем коэффициенты полинома   ,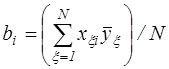

4) определяем значимость найденных коэффициентов по критерию Стьюдента

t_T = 2,31, при n = N (n –1) = 8 и р = 0,05.

    , ,

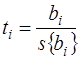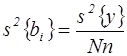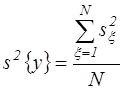
Если t₁₂₃ < t_T,  то коэффициент b₁₂₃ является незначимым. Таким образом, математическое описание функции отклика заданной области имеет вид полинома.

Дисперсия адекватности определяется из выражения

                               ,

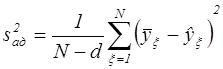Если 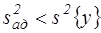, то можно сделать вывод:

разработанная математическая модель адекватна исследуемо­му технологическому процессу и может использоваться в заданной области для оптимизации его параметров.

Исходные данные для расчета:

Технологическая операция: термическое окисление кремния.

Статистические данные выборок

у1	85	35	88	92	73	41	54	71
у2	93	26	90	77	82	26	46	70

Курсовая работа

Цель - построение математической модели обтекания клина сверхзвуковым потоком. Предложить численную методику решения, основанную на конечно-разностных схемах.

   Исходные данные: Уравнения, описывающие невязкий двумерный или осесимметричный поток в области между телом (клином) и ударной волной, представлены в виде

 

где r - плотность, Р – давление, u, v – компоненты скорости вдоль осей x и y соответственно, g - отношение удельных теплоемкостей, b _к – угол полураствора тела, а s равно 0 для двумерного течения и 1 для осесимметричного. 

Граничные условия: На отошедшей от обтекаемого тела ударной волне заданы соотношения Ренкина-Гюгонио:

 

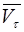- вектор скорости, лежащий в плоскости, касательной к поверхности ударной волны.

Индекс s относится к параметрам за ударной волной , v_n – нормальная составляющая скорости к поверхности ударной волны, D_n – скорость движения ударной волны.

На поверхности тела:

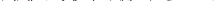Задание: Разработать теоретическую модель сверхзвуковых течений на ограниченном по протяженности участке поверхности обтекаемого тела . Задачу стационарного сверхзвукового обтекания тела решить методом установления.

Курсовая работа

Вероятность разорения представляет фундаментальный интерес для компании и служит основой для принятия важнейших решений. Для ее расчета в актуальной математике разработан целый ряд моделей разной степени сложности.

Тема: Построение модели разорения финансово-страховой компании.

Анализ простейшей модели базируется на следующих предположениях:

1. анализируется фиксированный относительно короткий (так что можно пренебречь инфляцией и не учитывать  доход от инвестирования) промежуток времени обычно это один год;

2. число договоров страхования N фиксировано и неслучайно;

3. плата за страховку полностью вносится в начале анализируемого периода; никаких поступлений в течение этого периода нет;

4.  наблюдаем каждый отдельный договор страхования и знаем статистические свойства связанного с ним индивидуального иска Х (поскольку не все договора приводят к иску, некоторые из случайных величин Х1,… ,Х N ,где Хi -  иск от i-го договора, равны нулю).

В рамках этой модели разорение определяется суммарным иском      S=X1+….+XN  к страховой компании. Если этот суммарный иск больше, чем капитал компании, то компания не сможет выполнить свои обязательства и разориться.

Поэтому вероятность разорения компании равна R=P{X1+…+XN > u}.

В качестве основной характеристики портфеля рассматривается общее число исков n за анализируемый период. Следует отметить, что n является случайной величиной и хорошо описывается с помощью пуассоновского распределения.

Предполагается одинаковая распределенность случайных величин Y1,Y2 …, описывающих величины последовательных реально поступивших исков. Иски рассматриваются как следствие общего риска компании. Разорение определяется суммарным иском:    S=Y1+…+Y n ,  вероятность разорения компании      R=P{Y1+…+Y n > u},  u- капитал компании.

Исходные данные: ПУАССОНОВСКОЕ РАСПРЕДЕЛЕНИЕ.

Свойство 1.

Предположим, что мы имеем несколько независимых групп договоров страхования; поступление исков от i-й группы за анализируемый промежуток времени описывается пуассоновской величиной со средним l i, а величина предъявляемого иска имеет распределение Fi(x). Тогда, если мы объединим все договора в одну большую группу, то поступление исков от этого суммарного портфеля будет характеризоваться распределением Пуассона со средним l = l 1+ l 2+…, а величина предъявляемого иска будет иметь распределение F(x), являющееся средним с весами l i/ l значением распределений Fi(x).

В такой формулировке результат очевиден интуитивно:

1. i-й портфель за рассматриваемый период произведет в среднем li исков; поэтому объединенный портфель произведет в среднем l = l 1+ l 2+… исков;

2.если поступил иск от объединенного портфеля, то с вероятностью li/l он порожден i-м составляющим портфеля и поэтому имеет распределение

 

.

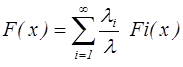Свойство 2.

Предположим, что случайная величина S имеет составное пуассоновское распределение с параметрами l и F(x) . Допусти, что распределение величины предъявляемого иска представлено в виде смеси с весами р1,р2…. распределений Fi(x):

.

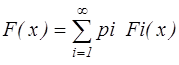Тогда S совпадает по распределению с суммой независимых случайных величин S1,S2,… , каждое из которых имеет составное пуассоновское распределение с параметрами l i = l pi и Fi(x) , i =1,2,…

Применяя свойство 2, мы можем рассматривать исходный суммарный иск S  как сумму k суммарных исков S1,…,Sk с параметрами l р1, …, l р k и детерминированными величинами исков.

Задание

Предположим, что страховая компания заключила N=10000 договоров страхования жизни сроком на один год на следующих условиях: в случае смерти застрахованного в течении одного года от несчастного случая компания выплачивает наследникам 1000000руб., а в случае смерти в течении одного года от естественных причин - 250000руб. Компания на платит ничего ,если застрахованный не умрет в течении одного года. Вероятность смерти от несчастного случая 0,0005. Вероятность смерти от естественных причин в зависимости от возраста. N1=4000, с вероятностью смерти в течении года q1=0,0040; N2=6000, q2=0,0020.

Определить зависимость вероятности разорения от величины резервов компании.

 

ЗАКЛЮЧЕНИЕ

Итак, вы познакомились с предложенным вам практическим пособием. Однако не стоит думать, что вы сразу же познали все азы новой для вас студенческой жизни. Все, что вы узнали из нашего пособия, вам придется постигать и применять на практи­ке на протяжении всего периода обучения в вузе. Но мы, авторы, надеемся, что с помощью нашей методички вам будет намного легче учиться, что она станет вам надежным и полезным помощником. Читая методические указания, следует помнить, что она не содержит готовых рецептов на все случаи научного творчества. Все дающие в ней советы и рекомендации являются наиболее общими, требующими индивидуальной корректировки в соответствии и с характером и тематической направленностью выполняемой курсовой работы. При работе над этим пособием, авторами использованы не только зна­ния, полученные из разных книг, но и свой многолетний опыт — как студенческий, так и преподавательский, а также опыт многих наших студентов, аспирантов и коллег-преподавателей. Поэтому не случайно каж­дая часть пособия содержит много реко­мендаций, которые помогут вам научиться учиться, правильно организовать свою учебную и научную работу.