Правильно определить уровень кредитного риска – достаточно сложная задача, решение которой невозможно без применения специальных методов количественной оценки и соответствующего математического аппарата. Поскольку во многих определениях понятие «риск» рассматривается как явление, подчиняющееся определенным математическим законам, то вполне обосновано изучать методы измерения банковского кредитного риска с позиций двух математических теорий: теорий игр и теории вероятностей.

В теории игр риск оценивается рядом взаимосвязанных критериев, основные из которых охарактеризованы в работах отечественных и зарубежных авторов.

Например, критерий Вальда предусматривает выбор самой осторожной пессимистической стратегии. Критерий Лапласа предполагает равновероятным наступление любого возможного варианта. Критерий Байеса применяется в случаях неопределенности при известном распределении вероятностей возможных состояний. Критерий Кофмана основан на применении понятий «неудача» и «успех». Критерий Ходжеса – Лемана предполагает использование двух субъективных показателей: параметра оатимизма из критерия Гурвица и распределения вероятностей по критерию Байеса. Для оценки риска инвестиционных проектов наиболее применим критерий Сэвиджа, который предусматривает минимизацию упущенной выгоды.

Однако в большинстве случаев при измерении кредитного риска в качестве методологической основы принимаются вероятностные расчеты. Возможность наступления тех или иных рисковых событий можно определять с помощью приемов математической теории вероятностей. Выделяют три взаимодополняемых метода измерения кредитного риска.

Точный вероятностый метод. Он считается наиболее предпочтительным, когда имеется надежная информация о всех сценариях развития событий и их вероятностях.

Приближенный вероятностный метод. В случае, когда по каким-либо причинам не удается определить искомое распределение вероятностей для множества всех сценариев, оправданным является сознательное упрощение этого множества в расчете на то, что полученная, хотя и грубая, модель окажется все-таки практически полезной.

Косвенный (качественный) метод. Если применение точной или приближенной вероятностных моделей оказывается практически невозможным, значит, количественное измерение риска недостижимо. В этом случае целесообразно ограничится измерением каких-либо других показателей, косвенно характеризующих данный риск и одновременно доступных для практического применения. Несмотря на то, что данный метод дает всего лишь качественную оценку, тем не менее, в ряде случаев он оказывается единственно возможным.

Как правило, в банке всегда испытывается определенный недостаток информации о поведении тех или иных заемщиков с точки зрения их добросовестного отношения к выполнению условий кредитного договора. В данном случае кредитный работник может воспользоваться вероятностным методом измерения кредитного риска.

В практике кредитования обычно встречаются три наиболее типичные ситуации:

* заемщик первый раз обращается за кредитом в банк, то есть кредитная история полностью отсутствует;

* заемщик много раз брал кредиты и всегда своевременно и в полном объеме их возвращал;

* заемщик много раз брал кредиты, но не всегда своевременно и в полном объеме их возвращал.

Рассмотрим каждую из трех ситуаций с позиции математической теории вероятностей.

В первом случае, когда данные о репутации заемщика отсутствуют, и кредитные отношения с ним банк оформляет в первый раз, целесообразно пользоваться принципом «fifty-fifty» (50 на 50), то есть вероятность возврата кредита равна вероятности невозврата.

Во втором случае, когда заемщик много раз пользовался кредитными услугами банка и всегда своевременно и в полном объеме выполнял взятые на себя обязательства, может сложиться мнение, что риски в отношении этого заемщика отсутствуют вовсе. Однако на практике это не всегда так.

Среднее значение вероятности невозврата кредита (Q) в данном случае рассчитывается по формуле

Q = 1 / (n + 1),

где n – количество предоставленных ранее кредитов.

В свою очередь, вероятность возврата кредита (P) рассчитывается по формуле P = 1 – Q.

Дисперсия для Q равна D (Q) = PQ / (n + 2).

С каждым полученным и возвращенным своевременно и в полном объеме кредитом вероятность невозврата долга конкретным заемщиком уменьшается. Вместе с тем даже длительная положительная кредитная история заемщика, не содержащая каких-либо отрицательных сведений о нем, не освобождает банк от кредитного риска в полной мере.

Третий случай характеризуется ситуацией, когда заемщик имеет в целом положительную кредитную историю, однако существует также и негативная информация. Она может касаться задержки платежей по основному долгу или процентам, отдельных случаев нецелевого использования полученных в прошлом кредитов и других нарушений обязательств заемщиком.

В данном случае среднее значение вероятности невозврата кредита заемщиком достаточно легко рассчитать по следующей формуле:

Q = (m + 1) / (n + 1),

где m – число нарушений заемщиком условий договоров с банком.

Вероятность возврата кредита и дисперсия для Q рассчитываются по формулам, аналогичным указанным выше.

Наглядная характеристика рассмотренных ситуаций и расчета вероятности невозврата кредитов конкретным заемщиком приведена в таблице А.1 [Приложение А].

Для измерения банковского кредитного риска может использоваться приближенный вероятностный метод, основанный на сведении множества возможных сценариев к бинарному распределению.

· клиент не выполнит свои обязательства, в результате чего банк потеряет сумму L;

· клиент выполнит свои обязательства, и банк получит некоторую прибыль F.

Оценка параметров L и F в данной модели выполняется сравнительно просто: потери равны сумме кредитов, а прибыль – это доход в соответствии с условиями договора.

С целью измерения риска конкретной кредитной операции целесообразно оценивать параметр наиболее ожидаемого результата (re) по формуле математического ожидания:

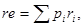
где 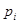 – вероятность 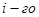результата;  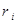– 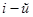возможный результат от операции.

Количественной оценкой риска конкретной кредитной операции принято считать вариацию (var), то есть разброс возможных результатов операции относительно ожидаемого значения (математического ожидания). В соответствии с теорией вероятности этот показатель рассчитывается как среднее квадратичное отклонение от ожидаемого результата по формуле:

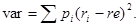
Кроме того, для оценки и измерения риска используется показатель среднего линейного отклонения, или дисперсии :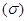

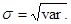
Кредитный риск в данном случае будет измеряться на базе данных среднего линейного отклонения и наиболее ожидаемого результата от операции путем их соотношения с помощью показателя стандартного отклонения. Формула расчета имеет вид:

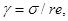
где 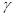 - стандартное отклонение.

Чем выше уровень данного показателя, тем более высокий кредитный риск у оцениваемой операции.

Приближенный вероятностный метод измерения риска, а также описанные выше формулы расчета показателей, характеризующих кредитный риск, целесообразно использовать при сравнении различных альтернатив вложения средств.

В практике измерения банковского кредитного риска банковским работникам приходится сталкиваться и с ситуациями, когда необходимо рассчитать вероятность невыполнения своих обязательств не одним, а сразу несколькими заемщиками одновременно. Для этого необходимо воспользоваться формулой Пуассона, поскольку вероятность невозврата долга крайне незначительна. Формула Пуассона имеет вид:

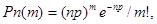
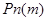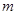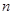где - вероятность наступления события раз в испытаниях; 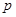- вероятность наступления события в единичном испытании; 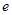- число, равное 2,718.

Измерить уровень кредитного риска можно также с помощью данных выборочного наблюдения за частотой невозвратов или потерь ссуженных средств. Однако даже самые обширные сведения о случаях кредитных потерь не способны в полной мере определить уровень кредитного риска в будущем. Поэтому всю совокупность сведений о наступлении случайного события и его частоте необходимо рассматривать как некоторую выборку, для которой обязательно должна быть рассчитана так называемая ошибка выборки.

Предельная ошибка выборки рассчитывается по следующей формуле:

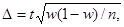
где 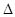- предельная ошибка выборки;  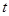- кратность ошибки, связывающая размер ошибки с заданной вероятностью;  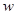- выборочная доля или частота наступления события в эксперименте;  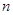- объем выборки.

Верхняя граница интервала изменения вероятности кредитных потерь (Lh) с учетом предельной ошибки выборки находится по формуле:

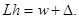
Рассмотренные экономико-математические методы отражают объективную вероятность риска и используются при наличии информации о статистике банкротств или потерь по кредитам. Когда нет таких данных и рассчитать объективную вероятность рискового события не представляется возможным, возникает необходимость применения иных методов, основанных на субъективной оценке риска.

Косвенные (качественные) методы измерения банковского кредитного риска строятся главным образом на основе метода экспертных оценок.

Данный метод используется при необходимости решения сложных, нестандартных экономических задач, требующих подключения интеллектуального потенциала профессионалов, а также в случае, когда мнение экспертов выступает практически единственным источником информации.

Метод экспертных оценок предполагает наличие определенной технологии опроса экспертов и обработки полученных сведений. Технология проведения экспертной оценки включает в себя следующие этапы:

· формирование группы экспертов;

· организацию опроса экспертов;

· анализ экспертных оценок;

· подведение итогов работы экспертов и подготовку комплексного заключения по проблеме.

Удачное формирование группы экспертов зависит от многих факторов, в частности, от степени компетентности каждого эксперта в подлежащей рассмотрению проблеме, креативности или способности к нестандартным подходам к проблеме, занимаемой должности, от опыта работы по специальности в качестве эксперта, наличия ученой степени, научных трудов, публикаций и так далее.

При формировании группы экспертов приходится решать разные проблемы. Во-первых, круг высококлассных специалистов в любой области знаний существенно ограничен. Во-вторых, среди претендентов могут быть хорошие специалисты в своей области, но одновременно не желающие раскрывать свои профессиональные секреты, представляющиеся для них особо ценными. Еще одна существенная проблема – определение количественного состава группы. С одной стороны, недостаточное количество экспертов лишает процедуру групповой экспертной оценки всякого смысла, а с другой – большое их количество может привести к трудностям при обработке данных. При выборе экспертов лучше всего руководствоваться соображениями их компетентности.

Следующий этап технологии экспертной оценки – организация опроса экспертов.

Считается, что специфика методов экспертного опроса определяется природой экспертных заключений, то есть в большинстве случаев эксперт мыслит не числами, а вербальными образами. Это значит, что требовать от него точной количественной оценки процесса или явления практически невозможно, так как это может привести к искажению окончательных выводов. Особое значение рекомендуется придавать формулировкам вопросов, на которые эксперт должен ответить. Не следует, например, составлять сложные, объемные вопросы, потому что эксперту легче дать точный ответ на большое количество простых вопросов, чем отвечать на несколько сложных. При этом, чем квалифицированнее эксперт, тем большую трудность для него составляют «неоднозначные» вопросы. Формализация индивидуальных оценок эксперта может осуществляться по следующей формуле:

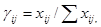
где 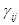 - нормированная оценка j-м экспертом i-го фактора;  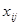- абсолютная оценка j – м экспертом i – го фактора, баллы; m – количество оцениваемых факторов; n – количество экспертов.

Процедура опроса обычно проходит в несколько этапов в зависимости от целей оценки, располагаемых средств, промежуточных результатов. На первом этапе опрос осуществляется независимо и без требований аргументации оценок. На втором этапе эксперты получают информацию о крайних оценках. Им предоставляется возможность корректировки своих заключений. На последующих этапах экспертам сообщаются усредненные оценки, после чего они могут вновь изменить свое мнение, предварительно аргументировав его. Практика показывает, что после 3 – 5 этапов опроса выводы экспертов становятся стабильными, что является сигналом для прекращения опроса и перехода к анализу экспертных оценок.

В силу того, что эксперт хорошо разбирается в предметной области, он способен выделить наиболее важные аспекты проблемы. Вместе с тем произвести комплексную оценку, сделать определенные итоговые выводы, особенно если требуется получить численные показатели, ему сложно. Эта задача решается при помощи формализованных методик анализа экспертных оценок.

Анализ экспертных оценок проводится на основе специальных математических теорий и методик. К их числу следует отнести теорию анализа иерархий, нечисловую статистику, многокритериальную оптимизацию, анализ предпочтений и другие.

Анализ экспертных оценок включает два стандартных этапа:

· анализ согласованности экспертных оценок и выявление «некомпетентных» экспертов;

· усреднение экспертных оценок.

Задачей первого этапа является достижение согласованности экспертных оценок. Так, может оказаться, что мнения экспертов по одним и тем же вопросам существенно расходятся. В такой ситуации проводить усреднение оценок экспертов для формирования окончательных выводов не представляется возможным, поэтому применяется процедура выявления «некомпетентных» экспертов.

Как правило, субъективные оценки «некомпетентных» экспертов резко выделяются из совокупности всех оценок. Поэтому анкеты таких экспертов исключаются из дальнейшего рассмотрения.

В случае достижения согласованности экспертных оценок переходят ко второму этапу, когда экспертные оценки обрабатываются, и происходит их усреднение. В результате, как правило, удается найти итоговое, наиболее оптимальное решение проблемы, которое наилучшим образом согласуется с индивидуальными выводами экспертов. При помощи формул данная процедура приобретает следующий вид:

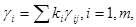
где 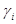 - групповая (итоговая) оценка экспертов;  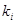- коэффициент компетентного j –го эксперта.

При этом коэффициент компетентности экспертов удовлетворяет следующей формуле:

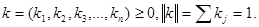
Подведение итогов работы экспертов и подготовка комплексного заключения по проблеме – заключительный этап технологии экспертной оценки. После его завершения группа экспертов расформировывается, а инициатор проведения экспертизы, которым выступает банк, получает наиболее приемлемый вариант решения стоящих перед ним задач и определенный опыт применения методов экспертной оценки.

Таким образом, использование специальных экономико-математических методов для измерения банковского кредитного риска в настоящее время рассматривается банковскими специалистами не просто как рекомендация по более эффективному управлению рисками, а как ярко выраженная потребность и необходимое условие адекватной оценки и измерения риска, от правильности проведения которых зависит результативность деятельности кредитного учреждения [16, с. 153 - 167].