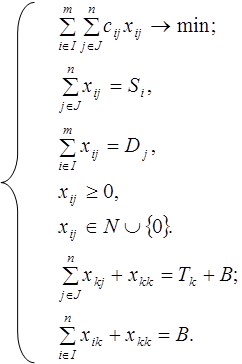Одно практически важное обобщение классической транспортной задачи связано с учетом возможности доставки товара от i-го источника к j-му стоку по маршруту, проходящему через некоторый промежуточный пункт (склад). Так, например, промежуточные пункты являются составной частью распределительной системы любой крупной компании, имеющей сеть универсальных магазинов во многих городах. Такая компания обычно имеет зональные оптовые базы (источники), снабжающие товарами более мелкие региональные склады (промежуточные пункты), откуда эти товары поступают в розничную торговую сеть (стоки). При этом товар для каждого фиксированного стока в общем случае может быть доставлен не из любого источника и по маршрутам, не обязательно проходящим через все промежуточные пункты. Кроме того, промежуточные пункты могут обладать вполне определенной спецификой. Так, например, при транспортировке товара от источника к стоку по маршруту, проходящему через склад, часть товара может быть использована для создания неприкосновенного запаса на складе.
Задачу выбора плана перевозок товаров от источников стокам с учетом промежуточных пунктов, обеспечивающего минимальные транспортные затраты и потребности стоков, в исследовании операций называют транспортной задачей с промежуточными пунктами. Для приобретения практических навыков в построении математических моделей таких задач обратимся к следующему примеру.
На рисунке 4 представлена схема размещения складов, на которой указаны: а) склады в виде узлов сети с номерами от 1 до 6; б) избыток товара на складе, который должен быть перераспределен в системе складов (указан в квадратных скобках рядом с узлом сети положительным числом и выражен в единицах измерения товара); в) недостаток товара на складе, который должен быть устранен за счет его поставок с других складов системы (указан в квадратных скобках рядом с узлом сети отрицательным числом).
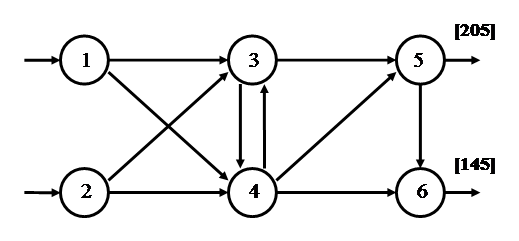
Рисунок 4 – Схема размещения складов
На рисунке 4 видно, что суммарный избыток товара, имеющийся на складах системы с номерами 1 и 2, равен суммарному недостатку товара, имеющемуся на складах с номерами 5, 6. Перераспределение товара может происходить через склады с номерами 3 и 4, которые в рассматриваемой задаче и являются промежуточными или транзитными пунктами. Истинными пунктами отправления являются лишь склады с номерами 1 и 2, на которых имеется избыток товара и с которых товар можно только вывозить, а истинным пунктом назначения является склад с номером 6, на котором есть недостаток товара, и на этот склад товары можно только завозить. Заметим также, что между складами с номерами 3 и 4 возможны перевозки в обоих направлениях, но в общем случае c34¹c43 (например, наличие одностороннего движения по кратчайшему маршруту). Объемы спроса и предложения, соответствующие этим пунктам отправления и назначения, вычисляются следующим образом.
Объем предложения истинного пункта отправления = объем исходного предложения.
Объем предложения транзитного пункта = объем исходного предложения + объем буфера.
Объем спроса истинного пункта назначения = объем исходного спроса.
Объем спроса транзитного пункта = объем буфера.
Объем буфера должен быть таким, чтобы вместить объем всего предложения (или спроса).
Пусть J — множество номеров складов, на которые товар может быть доставлен с k-го склада, а I — множество номеров складов, с которых товар может быть доставлен на k-й склад. T
k — величина чистого запаса товара, равная объему исходного предложения или исходного спроса. Тогда математическую модель данной задачи можно представить следующим образом: