Лабораторная работа №8 (4 часа). Сортировки методом прямого обмена и с помощью дерева.
Цель работы:
- исследовать и изучить методы сортировки с помощью прямого обмена и с помощью дерева;
- овладеть умениями и навыками написания на языке программирования С++ программ сортировки с использованием прямого обмена.
Порядок выполнения работы
- ознакомиться с краткой теорией и примерами решения задач, относящихся к сортировкам методом прямого обмена и с помощью дерева;
- ответить на контрольные вопросы и получить оценку по знанию теории;
- получить задание на выполнение конкретного варианта лабораторной работы и выполнить его;
- написать и отладить программу решения задачи на языке С++;
- составить отчет по лабораторной работе и защитить его у преподавателя.
Содержание отчета по ЛР
- наименование ЛР и ее цель;
- задание на ЛР согласно варианту;
- листинг приложения, обеспечивающей успешное решение студентом полученного варианта задачи;
- результаты работы программы.
Краткая теория
В предыдущей лабораторной работе оба разбиравшихся метода сортировки рассматривать как "обменные" сортировки. В данном разделе описан метод, где обмен местами двух элементов представляет собой характернейшую особенность процесса. Изложенный ниже алгоритм прямого обмена основывается на сравнении и смене мест для пары соседних элементов и продолжении этого процесса до тех пор, пока не будут упорядочены все элементы.
Сортировка методом прямого обмена (Пузырьковая сортировка).
Как в методе прямого выбора, мы повторяем проходы по массиву, сдвигая каждый раз наименьший элемент оставшейся последовательности к левому концу массива. Будем рассмтривать массив из n элементов, причем не горизонтальный, а вертикальный, тогда элементы можно интерпритировать как пузырьки в чане с водой, причем вес каждого соответствует его ключу. Массив проходится (n -1) раз сверху вниз, при этом элементы попарно сравниваются, если нижний элемент меньше верхнего, то элементы переставляются.
Алгоритмы
Алгорим метода прямого обмена (пузырковой сортировки) в псевдокоде следующий:
for i = 2 to n
for j = n to i step -1
if a(j) < a(j - 1) then
x = a(j - 1)
a(j - 1) = a(j)
a(j) = x
endif
next j
next i
return
Рассмотрим пример.
Пусть дан массив из следующих элементов: 4, 3, 7, 2, 1, 6.
На нижеприведенном рисунке изображена иллюстрация алгоритма пузырьковой сортировки для рассматриваемого массива.

В данном случае получился один проход “вхолостую”. Чтобы лишний раз не просматривать элементы, а, значит, не проводить сравнения, затрачивая на это время, можно ввести флажок fl, который остается в значении false , если при очередном проходе не будет произведено ни одного обмена. Ниже приведен усовершенствованный алгоритм.
fl = true
for i = 2 to n
if fl = false then return
endif
fl = false
for j = n to i step -1
if a(j) < a(j - 1) then
fl = true
x = a(j - 1)
a(j - 1) = a(j)
a(j) = x
endif
next j
next i
return
Еще одним усовершенствованием алгоритма является так называемая шейкерная сортировка, где после каждого прохода меняется направление во внутреннем цикле.
В случае, если реализовывать алгоритм пузырьковой сортировки без усовершенствований, то
Количество сравнений: 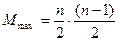
Количество перемещений: 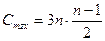
Из приведенных расчетов следует, что эффективность сортировки данным методом также имеет порядок n 2 .
В классическом виде сортировка методом прямого обмена (пузырьковая) представляет собой нечто среднее между сортировками с помощью включений и с помощью выбора. Если же в нее внесены приведенные выше усовершенствования, то для достаточно упорядоченных массивов пузырьковая сортировка даже имеет преимущество. К преимуществам пузырьковой сортировки можно также отнести простоту алгоритма ее реализации.
Прежде чем переходить к методам реализации алгоритмов пузырьковой сортировки на языке С++, рассмотрим еще один метод сортировки. Все вышерассмотренные сортировки производились на статистических структурах без динамического выделения памяти. Однако в некоторых случаях сортировка может быть более эффективной, если для ее реализации использовать динамические структуры данных. Естественно, в этом случае усложняется сам алгоритм сортировки. Одним из таких методов является сортировка с помощью бинарного дерева.
В лабораторной работе № 3 были подробно рассмотрены алгоритмы создания и обхода сбалансированного бинарного дерева. Если сортируемые элементы являются целыми числами, и при занесении их в память машины они будут являтся ключами создаваемого сбалансированного бинарного дерева, то при обходе полученного дерева слева направо получим отсортированный по возрастанию массив.
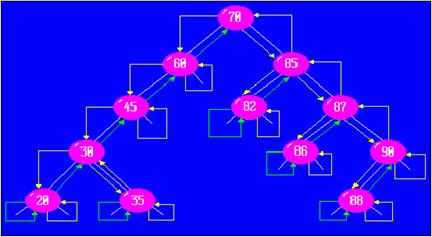
Пусть в первоначально пустой массив заносятся последовательно поступающие элементы: 70, 60, 85, 87, 90, 45, 30, 88, 35, 20, 86.
При обходе дерева слева - направо получаем отсортированный массив 20, 30, 35, 45, 60, 70, 82, 85, 86, 87, 88, 90. Элемент дерева заносится в массив при втором заходе в него (на рисунке вторые заходы показаны зелеными стрелками).
Алгоритмы создания и обхода слева направо в псевдокоде и на языке С++ упорядоченного бинарного дерева здесь не представлены, поскольку они подробно описаны в лабораторной работе № 3.
Теперь вернемся к сортировке методом прямого обмена (пузырьковой) и рассмотрим листинги реализации программ
Контрольные вопросы по теории (сортировка с помощью обмена).
1. Сколько сравнений и перестановок элементов требуется в пузырьковой сортировке?
- n * lon ( n );
- ( n * n )/4;
- ( n * n - n )/2.
2. Сколько дополнительных переменных нужно в пузырьковой сортировке помимо массива, содержащего элементы?
- 0 (не нужно);
- всего 1 элемент;
- n переменных (ровно столько, сколько элементов в массиве).
3. Как рассортировать массив быстрее, пользуясь пузырьковым методом?
- одинаково;
- по возрастанию элементов;
- по убыванию элементов.
4. Массив сортируется “пузырьковым” методом. За сколько проходов по массиву самый “лёгкий” элемент в массиве окажется вверху?
- за 1 проход;
- за n-1 проходов;
- за n проходов, где n – число элементов массива.
5. При обходе дерева

- слева направо получаем последовательность…
- отсортированную по убыванию;
- не отсортированную;
- отсортированную по возрастанию.
6. При обходе дерева слева направо его элемент заносится в массив…
- при втором заходе в элемент;
- при первом заходе в элемент;
- при третьем заходе в элемент.
7. Элемент массива с ключом k=20 необходимо вставить в изображённое дерево так, чтобы дерево осталось отсортированным. Куда его нужно вставить?
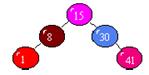
- левым сыном элемента 30;
- левым сыном элемента 41;
- левым сыном элемента 8.
8. При обходе какого дерева слева направо получается отсортированный по возрастанию массив?
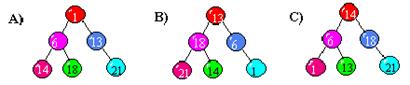
- A ;
- B ;
- C .
Примеры алгоритмов конкретных задач
Рассмотрим теперь реализацию функций сортировки методом пузырька и его усовершенствований на С++ и примеры сортировки конкретных числовых массивов.
/* **************************************************** */
/* СОРТИРОВКА МЕТОДОМ ПУЗЫРЬКА */
#include <stdio.h>
#include <conio.h>
#define n 8
int A[n] = {27,412,71,81,59,14,273,87};
/* ======================================= */
main()
{ void BblSort(int A[],int nn);
int j;
printf("\n Сортировка методом пузырька");
printf("\n Исходный массив \n");
for (j=0; j<n; j++)
printf("\t%d",A[j]);
printf("\n");
BblSort(A,n);
printf("\n Отсортированный массив \n");
for (j=0; j<n; j++)
printf("\t%d",A[j]);
printf("\n");
getch(); return 0;
}
/* =========================================== */
/* ФУНКЦИЯ СОРТИРОВКИ МЕТОДОМ ПУЗЫРЬКА */
void BblSort(int A[],int nn)
{ int i,j,k,p;
printf("\n Отладочная печать по шагам сортировки");
for ( i=0; i<nn-1; i++ )
{ p = 0;
for (j=nn-1; j>i; j--)
if (A[j] <A[j-1])
{ k = A[j]; A[j] = A[j-1]; A[j-1] = k; p = 1;}
/* Если перестановок не было, то сортировка выполнена */
if ( p == 0)
break;
printf(" \ni = %d",i);
for (j=0; j<nn;j++)
printf("\t %d",A[j]);
}
}
/* ****************************************************** */
В данном примере функция сортировки методом пузырька BblSort описана таким образом, чтобы “холостых” проходов не было.
В заключительном листинге представлена программе сортировки того же массива с помощью функции Шейкерной сортировки, которая является усовершенствованием пузырьковой.
/* *************************************************** */
/*ШЕЙКЕРНАЯ СОРТИРОВКА. */
#include <stdio.h>
#include <conio.h>
#define n 8
int A[n] = {27,412,71,81,59,14,273,87};
/* ====================================== */
main()
{ void ShkrSort(int A[],int nn);
int j;
printf("\n Шейкерная сортировка");
printf("\n Исходный массив: \n");
for (j=0; j<n; j++)
printf("%d\t",A[j]);
printf("\n");
ShkrSort(A,n);
printf("\n Отсортированный массив :\n");
for (j=0; j<n; j++)
printf("%d\t",A[j]);
printf("\n");
getch(); return 0;
}
/* ====================================== */
/* ФУНКЦИЯ ШЕЙКЕРНОЙ СОРТИРОВКИ */
void ShkrSort(int A[],int nn)
{ int i,j,k,x,L,R;
L = 1; R = nn-1; k = nn-1;
printf("\n Отладочная печать");
do
{
for ( j=R; j>=L; j-- )
if ( A[j-1] > A[j] )
{ x = A[j-1]; A[j-1] = A[j]; A[j]=x; k=j; }
L = k + 1;
/* Отладочная печать */
printf(" \nL = %d",L);
for (i=0; i<nn; i++)
printf("\t%d",A[i]);
for (j=L; j<=R; j++)
if ( A[j-1] > A[j] )
{ x = A[j-1]; A[j-1] = A[j]; A[j] = x; k = j; }
R = k -1;
/* Отладочная печать */
printf(" \nR = %d",R);
for (i=0; i<nn; i++)
printf("\t%d",A[i]);
}
while ( L < R );
}
/* *********************************************** */
Задания
1. На заводе выпустили детали со следующими серийными номерами: 45, 56, 13, 75, 14, 18, 43, 11, 52, 12, 10, 36, 47, 9. Детали с четными номерами поступают на склад №1, а с нечетными на слад №2. Требуется отсортировать детали на складе №1.
2. Угнали автомобиль. Свидетель запомнил, что первой цифрой номера была 4. В базе угнанных автомобилей в этот день были следующие номера: 456, 124, 786, 435, 788, 444, 565, 127, 458, 322, 411, 531, 400, 546, 410. Нужно составить список номеров начинающихся на 4 и упорядочить его по возрастанию.
3. За неделю езды в транспорте накопились билеты с номерами 124512, 342351, 765891, 453122, 431350, 876432, 734626, 238651, 455734, 234987. Нужно отобрать "счастливые" билеты и расположить их по возрастанию.
4. Дан список людей с указанием их возраста. Для составления графика ухода сотрудников на пенсию требуется составить новый список новый список в том порядке, в каком они будут уходить на пенсию.
5. Студенты сдали пять экзаменов. Нужно отсортировать список студентов по возрастанию общего балла по результатам сданных экзаменов.
6. В городе был один автобусный парк, куда приезжали автобусы с номерами: 11, 32, 23, 12, 6, 52, 47, 63, 69, 50, 43, 28, 35, 33, 42, 56, 55, 101. После строительства второго автопарка решили перевести туда автобусы с нечетными номерами. Для того чтобы составить расписание их движения нужно организовать список номеров автобусов второго парка, упорядочив их по убыванию.
7. Была составлена ведомость по зарплате, представленная в виде: Иванов - 166000, Сидоров - 180000, ... Требуется упорядочить этот список таким образом, чтобы размер зарплаты уменьшался.
8. На стоянке стоят автомобили со следующими номерами: 1212, 3451, 7694, 4512, 4352, 8732, 7326, 2350, 4536, 2387, 5746, 6776, 4316, 1324. Для статистики необходимо составить список автомобилей с такими номерами, сумма первых двух цифр которых равна сумме двух последних цифр, так чтобы каждый следующий номер был меньше предыдущего.
9. Выпустили лотерейные билеты с четырехзначными номерами. Выигрышными считаются те билеты, сумма цифр которых делится на 4. Составить список выигрышных билетов, упорядоченных по убыванию.
10. Молодой человек взял номер телефона у своей знакомой, но забыл его. Он смог вспомнить только первые три цифры: 469***. В его записной книжке были следующие номера телефонов: 456765, 469465, 469321, 616312, 576567, 469563, 567564, 469129, 675665, 469873, 569090, 469999, 564321, 469010. Составить список номеров начинающихся с цифр 469 и упорядочить их по убыванию.
11.Студенты сдали пять экзаменов. Нужно отсортировать список студентов по убыванию общего балла по результатам сданных экзаменов.
12. Выпустили лотерейные билеты с четырехзначными номерами. Выигрышными считаются те билеты, сумма первых трех цифр которых равна 8. Составить список выигрышных билетов, упорядоченных по возрастанию.
Дата: 2019-12-10, просмотров: 527.