Удаление узла дерева не должно нарушать упорядоченность дерева. При удалении возможны 3 расположения узлов:
1) найденный узел является листом - он просто удаляется;
2) найденный узел имеет только сына - в этом случае сын перемещается на место удаленного отца;
3) у удаляемого отца два сына - в этом случае основная трудность состоит в удалении отца, поскольку в удаляемую вершину входит одна стрелка, а выходит две. В этом случае нужно найти подходящее звено поддерева, которое должно занять место удаляемого без нарушения упорядоченности дерева. Данным звеном может быть либо предшественник удаляемого узла, либо его приемник.
Предшественник - это самый правый элемент левого поддерева (для достижения этого элемента необходимо перейти в следующий узел по левой ветви, а затем двигаться только по правой ветви этого узла до тех пор, пока очередная ссылка не будет равна nil).
Приемник - это самый левый элемент правого поддерева (для достижения этого элемента необходимо перейти в следующий узел по правой ветви, а затем двигаться только по левой ветви этого узла до тех пор, пока очередная ссылка не будет равна nil).
Очевидно, что такие подходящие звенья могут иметь не более одной ветви.
На изображенном ниже рисунке проиллюстрированы возможные удаляемые из дерева узлы при трех возможных вариантах (лист (ключ 1), один сын (ключ 6), два сына (ключ 12)).
Предшественником удаляемого узла (12) является самый правый узел левого поддерева (11). Преемником узла (12) - самый левый узел правого поддерева (13).

Нижеприведенный в псевдокоде алгоритм разработан для поиска по дереву с удалением для всех трех возможных случаев нахождения узлов, причем в случае наличия у удаляемого узла двух сыновей его место занимает преемник (на рисунке узел 13 занимает место удаляемого узла 12).
Введем указатели:
p - рабочий указатель;
q - отстает от р на один шаг;
v - указывает на преемника удаляемого узла;
t - отстает от v на один шаг;
s - на один шаг впереди v (указывает на левого сына или пустое место).
В результате поиска преемника на узел 13 должен указывать указатель v, а указатель s - на пустое место (как показано на рисунке).
q = nil
p = tree
while (p <> nil) and (k(p) <> key) do
q = p
if key < k(p) then
p = left(p)
else
p = right(p)
endif
endwhile
if p = nil then ‘Ключ не найден’
return
endif
if left(p) = nil then v = right(p)
else if right(p) = nil
then v = left(p)
else
‘У nod(p) - два сына’
‘Введем два указателя (t отстает от v на 1 шаг, s - опережает)’
t = p
v = right(p)
s = left(v)
while s <> nil do
t = v
v = s
s = left(v)
endwhile
if t <> p then
‘v не является сыном p’
left(t) = right(v)
right(v) = right(p)
endif
left(v) = left(p)
endif
endif
if q = nil then ‘p - корень’
tree = v
else if p = left(q)
then left(q) = v
else right(q) = v
endif
endif
freenode ( p )
return
Контрольные вопросы по теории (поиск по дереву с включением)
Включение элемента в дерево
1. В каком дереве при бинарном поиске нужно перебрать в среднем N/2 элементов?
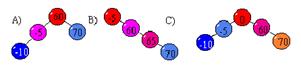
- A ;
- B ;
- C .
2. Сколько нужно перебрать элементов в сбалансированном дереве при бинарном поиске?
· A - N/2;;
· B - Ln(N);;
· C- Log2(N);;
· D - eN .
.
3. Выберете вариант дерева, полученного после вставки узла - 1.
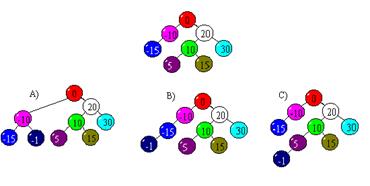
- A ;
- B ;
- C .
4. К какому элементу присоединить элемент 40 для вставки его в данное дерево?
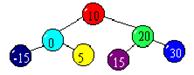
- к 30-му;
- к 15-му;
- к –15-му;
- к 5-му.
5. Какой вид примет дерево после вставки элемента с ключом 58?
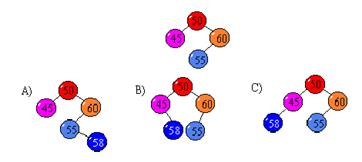
- A;
- B;
- C.
В. Исключение элемента из дерева
1. Выберете вариант дерева, полученного после удаления узла – 3.
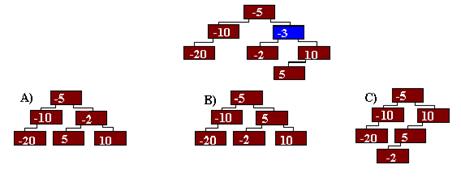
- A ;
- B ;
- C .
2. Какой вариант дерева получится после удаления элемента – 1, а затем – 8?
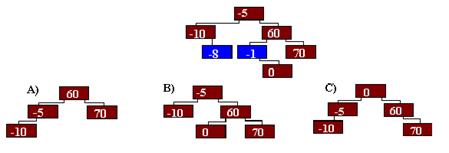
- A ;
- B ;
- C .
3. Выберете вариант дерева, полученного после удаления узла с индексом 0.
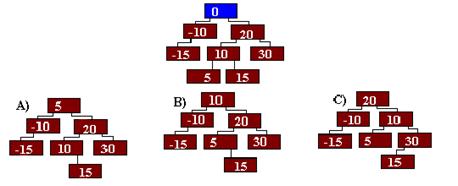
- A ;
- B ;
- C .
4. Какие из следующих пар чисел могут стать корнями дерева после удаления элемента 10 в соответствии с двумя способами удаления узла, имеющего двух сыновей?
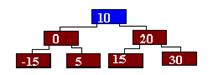
- 0 или 15;
- 0 или 20;
- 5 или 30;
- 5 или 15.
5. Какой вид примет дерево после удаления элемента с ключом 58?
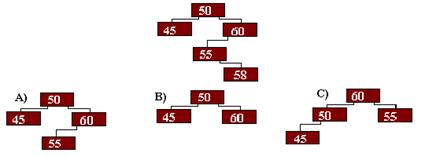
- A ;
- B ;
- C .
Примеры алгоритмов конкретных задач (поиск по дереву с включением, исключением)
Рассмотрим теперь, как реализуются алгоритмы поиска по дереву с включением и исключением на языке программирования С++.
Для простоты будем рассматривать бинарное упорядоченной дерево, в полях элементов которого ключи – вещественные числа, а поля записей отсутствуют. Описание самого элемента, функции создания и обхода подобного дерева подробно описаны в лабораторной работе № 3, поэтому здесь мы на них останавливаться не будем. Функция поиска со вставкой при уже созданном дереве будет иметь следующий вид:
void Vstavka ( double key ) //функция, вставляющая элемент в дерево
{Q=NULL;
P=tree;
while(P)
{ Q = P ;
if ( key == P -> k )
{ cout <<"\ n В дереве уже есть такой элемент, он найден, вставлять не надо\ n ";
return ;
/*если такой элемент в дереве уже есть, то функция завершает свою работу*/
}
if(key<P->k) P=P->left;
else P=P->right;
};
V=new element;
V->k=key;
V->left=V->right=NULL;
if(key<Q->k) Q->left=V;
else Q -> right = V ;
}
Функция поиска с удалением при уже созданном дереве будет иметь следующий вид:
void Poisk_Udalenie (double key) //функция поиска с удалением
{Q=NULL;
P=tree;
{ while(P&&P->k!=key)
{ Q=P;
if(key<P->k) P=P->left;
else P=P->right;
};
if(!P) { cout<<" Ключ не найден !"; return;};
if(P->left==NULL) V=P->right;
else
{if(P->right==NULL) V=P->left;
else
{ T=P;
V=P->right;
S=V->left;
while(S)
{ T=V;
V=S;
S=V->left;
};
if(T!=P) { T->left=V->right;
V->right=P->right;
}
V->left=P->left;
}
}
if(Q==NULL) tree=V;
else
if(P==Q->left) Q->left=V;
else Q->right=V;
delete P;
}
}
Теперь пример программы, в которой создается вышеописанное дерево и осуществляется вставка элемента в него
/*Поиск по дереву со вставкой, обходы слева направо */
#include<iostream.h>
#include<conio.h>
struct element
{ double k;
element* left;
element* right;
};
element *tree=NULL,*P,*Q, *V;
void maketree(double a)
{ if(!tree)
{ tree=new element;
tree->k=a;
tree->right=tree->left=NULL;
P=tree;
Q=NULL;
return;
};
P=Q=tree;
while (P!=NULL)
{ Q=P;
if(a<P->k) P=P->left; else P=P->right;
};
if(a<Q->k) { Q->left=new element;
Q->left->k=a;
Q->left->left=Q->left->right=NULL;
}
else { Q->right=new element;
Q->right->k=a;
Q->right->left=Q->right->right=NULL;
};
}
void Vstavka(double key) //функция вставляющая элемент в дерево
{
P=tree;
Q=NULL;
while(P)
{ Q=P;
if(key==P->k)
{cout<<"\n В дереве уже есть такой элемент, он найден, вставлять не надо\n";
return;
/*если такой элемент в дереве уже есть, то функция завершает свою работу*/
}
if(key<P->k) P=P->left;
else P=P->right;
};
V=new element;
V->k=key;
V->left=V->right=NULL;
if(key<Q->k) Q->left=V;
else Q->right=V;
}
void printree(element* tree)
{ if(tree)
{ printree(tree->left);
cout<<tree->k<<" ";
printree(tree->right);
};
}
void main()
{ clrscr();
double a,key;
cout<<"\n Введите элементы дерева, 0 - конец ввода: \n";
cin>>a;
while(a)
{ maketree(a);
cin>>a;
};
printree(tree);
cout<<endl<<" Введите ключ вставляемого элемента : ";
cin>>key;
Vstavka(key);
printree(tree);
getch ();
}
/*-------------------------------------------------------------------------------------- */
Следующий пример – программа создания бинарного дерева с последующим поиском и удалением найденного элемента
/*Поиск по дереву со вставкой, обходы слева направо */
#include<iostream.h>
#include<conio.h>
struct element
{ double k;
element* left;
element* right;
};
element *tree=NULL,*P,*Q, *V, *T, *S;
void maketree(double a) //функция, создающая (добавляющая) элемент в) дерево
{ if(!tree)
{ tree=new element;
tree->k=a;
tree->right=tree->left=NULL;
P=tree;
Q=NULL;
return;
};
P=Q=tree;
while (P!=NULL)
{ Q=P;
if(a<P->k) P=P->left; else P=P->right;
};
if(a<Q->k) { Q->left=new element;
Q->left->k=a;
Q->left->left=Q->left->right=NULL;
}
else { Q->right=new element;
Q->right->k=a;
Q->right->left=Q->right->right=NULL;
};
}
void Poisk_Udalenie (double key) // функция поиска с удалением
{
Q=NULL;
P=tree;
{ while(P&&P->k!=key)
{ Q=P;
if(key<P->k) P=P->left;
else P=P->right;
};
if(!P) { cout<<" Ключ не найден !"; return;};
if(P->left==NULL) V=P->right;
else
{if(P->right==NULL) V=P->left;
else
{ T=P;
V=P->right;
S=V->left;
while(S)
{ T=V;
V=S;
S=V->left;
};
if(T!=P) { T->left=V->right;
V->right=P->right;
}
V->left=P->left;
}
}
if(Q==NULL) tree=V;
else
if(P==Q->left) Q->left=V;
else Q->right=V;
delete P;
}
}
void printree ( element * tree )//функция вывода дерева на экран
{ if(tree)
{ printree(tree->left);
cout<<tree->k<<" ";
printree(tree->right);
};}
void main()
{ clrscr();
double a,key;
cout <<"\ n Введите элементы дерева, 0 - конец ввода: \ n ";
cin>>a;
while(a)
{ maketree(a);
cin>>a;
};
printree(tree);//печать дерева до удаления из него элемента
Q=NULL;
P=tree;
cout<<endl<<"Введите ключ удаляемого элемента: ";
cin>>key;
Poisk_Udalenie(key);
printree(tree);
getch();
}
/*-------------------------------------------------------------------------------------- */
Задания
Используя генератор случайных чисел сформировать бинарное дерево, состоящее из 15 элементов (предусмотреть ручной ввод элементов). Причем числа должны лежать в диапазоне от -99 до 99. Произвести поиск со вставкой и удалением элементов в соответствии со следующими вариантами заданий:
1. Числа кратные N.
2. Нечетные числа.
3. Числа > N.
4. Числа < N.
5. Числа по выбору.
6. Простые числа.
7. Составные числа.
8. Числа в интервале от X до Y.
9. Числа, сумма цифр (по модулю) которого > N.
10. Числа, сумма цифр (по модулю) которого < N.
11. Числа, сумма цифр (по модулю) которого лежит в интервале от X до Y.
12. Числа, взятые по модулю, квадратный корень которых целое число.
где: N, X, Y - задается преподавателем.
Дата: 2019-12-10, просмотров: 527.