Лаборторная работа №5 (4 часа). Исследование методов оптимизации поиска
Цель работы:
- исследовать и изучить методы поиска с перемещением в начало и транспозицией;
- овладеть умениями и навыками написания на С++ программ по исследованию методов поиска с перемещением в начало и транспозицией.
Порядок выполнения работы
- ознакомиться с краткой теорией и примерами решения задач, относящихся к методам оптимизации поиска;
- ответить на контрольные вопросы и получить оценку по знанию теории;
- получить задание на выполнение конкретного варианта лабораторной работы и выполнить его;
- написать и отладить программу решения задачи на языке С++;
- составить отчет по лабораторной работе и защитить его у преподавателя.
Содержание отчета по ЛР
- наименование ЛР и ее цель;
- задание на ЛР согласно варианту;
- листинг приложения, обеспечивающей успешное решение студентом полученного варианта задачи;
- результаты работы программы.
Краткая теория
Поиск (search) является одной из основ обработки данных в ЭВМ. Его назначение состоит в том, чтобы по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу или определить, что этих данных нет. Если этих данных нет, добавить их в массив данных.
Набор любых данных будем называть таблицей или файлом. Каждое данное или элемент структуры отличается каким-то признаком от других данных. Этот признак называется ключом. Ключ может быть уникальным, т.е. в таблице только одно данное с таким ключом, иначе уникальные ключи называются первичным ключом.
Вторичный ключ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных собраны в одном месте (таблице).
Ключи, которые выделены из таблицы данных и организованы в свой файл, называются внешним ключами. Если ключ в записи, то он называется внутренним ключом.
Поиск по заданному аргументу называется алгоритм, определяющий соответствие ключа данного с заданным аргументом. Результатом работы алгоритма поиска может быть нахождение этого данного или отсутствие данного в таблице. В случае отсутствия данного возможны две операции:
1. Индикация того, что данного нет.
2. Вставка данного в таблицу.
Пусть К - массив ключей, тогда для всех К(i) существует R(i) - данное. KEY - аргумент поиска. Ему соответствует информационная запись REC. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.
Переупорядочение таблицы поиска.
Всегда можно говорить о некотором значении вероятности нахождения того или иного элемента.
P(i) - вероятность нахождения элемента.
В этом случае таблица поиска представляется как система с дискретными состояниями, а искомый элемент характеризуется i-ым состоянием системы, вероятность которого P(i).
P(1) + P(2) + ... + P(n) = 1
Количество сравнений Z при поиске в таблице, т.е. количество сравнений, необходимых для поиска по заданному аргументу, представляет собой значение дискретной случайной величины, определяемой номерами состояний и вероятностями состояний системы.
Z=1*P(1) + 2*P(2) + 3*P(3) + ... + n*P(n)
Таблица данных должна быть упорядочена таким образом, чтобы в начале таблицы были элементы с большими вероятностями поиска или элементы, к которым чаще всего обращаются в таблице.
P(1) >= P(2) >= P(3) >= ... >= P(n)
Имеется два основных метода переупорядочивания таблиц поиска:
Алгоритмы
1) Переупорядочивание путем перестановки найденного элемента в начало списка.
2) Метод транспозиции.
Алгоритм переупорядочивания путем перестановки найденного элемента в начало списка.
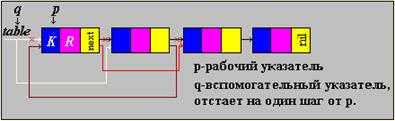
Найденный элемент сразу оказывается в голове списка.
На рисунке проиллюстрирован случай, когда найденный элемент второй в списке. Первоначально указатель q нулевой, указатель p указывает на начало списка; p перемещается на второй элемент, а q на первый. Указатель начала списка (table) перемещается на второй элемент, а указатель второго элемента на третий. Таким образом, второй элемент перемещается на первое место.
Нижеприведенный алгоритм предусматривает возможность перестановки в начало списка любого по счету найденного элемента списка, а также случай, когда найденный элемент в списке первый и перестановка не нужна.
Пример программы переупорядочивания (на псевдокоде)
q= nil
p = table
while (p <> nil) do
if key = k(p) then
search = p
if q = nil
then 'перестановка не нужна'
return
endif
nxt(q) = nxt(p)
nxt(p) = table
table = p
return
endif
q = p
p = nxt(p)
endwhile
search = 0
return
Метод транспозиции
В данном методе найденный элемент переставляется на один элемент к голове списка. Если к этому элементу обращаются часто, то он, постепенно перемещаясь к началу списка, скоро окажется в его голове.
Этот метод удобен тем, что он эффективен не только в списковых структурах, но и в неупорядоченных массивах, т.к. меняются местами только два рядом стоящих элемента.
Будем использовать три указателя:
p - рабочий указатель, указывает на элемент.
q - вспомогательный указатель, отстает на один шаг от p.
s - вспомогательный указатель, отстает на два шага от p.
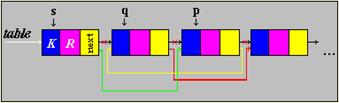
Рисунок иллюстрирует случай, когда найденный элемент третий в списке. Найденный нами третий элемент передвигается на один шаг к голове списка (т.е. становится вторым). Указатель первого элемента перемещается на третий элемент, указатель второго элемента на четвертый, таким образом, третий элемент перемещается на второе место. Если к данному элементу обратиться еще раз, то он окажется в голове списка.
Нижеприведенный алгоритм описывает метод транспозиции для любого по счету найденного элемента списка, а также случай, когда найденный элемент в списке первый и перестановка не нужна.
Пример программной реализации метода транспозиции (на псевдокоде)
s = nil
q = nil
p = table
while (p <> nil) do
if key = k(p) then
‘ нашли, транспонируем
if q = nil then
‘ переставлять не надо
return
endif
nxt ( q ) = nxt ( p )
nxt(p) = q
if s = nil then
table = p
else
nxt(s) = p
search = p
endif
return
endif
s =q
q = p
p = nxt(p)
endwhile
search = nil
return
Контрольные вопросы по теории (поиск с перемещением в начало и транспозицией)
1. Где наиболее эффективен метод транспозиций?
- в массивах и в списках;
- только в массивах;
- только в списках.
2. В чём суть метода перестановки ?
- найденный элемент помещается в голову списка;
- найденный элемент помещается в конец списка;
- найденный элемент меняется местами с последующим.
3. В чём суть метода транспозиции ?
- перестановка местами соседних элементов;
- нахождение одинаковых элементов;
- перестановка найденного элемента на одну позицию в сторону начала списка.
4. Что такое уникальный ключ ?
- если разность значений двух данных равна ключу;
- если сумма значений двух данных равна ключу;
- если в таблице есть только одно данное с таким ключом.
5. В чём состоит назначение поиска ?
среди массива данных найти те данные, которые соответствуют заданному аргументу;
определить, что данных в массиве нет;
с помощью данных найти аргумент.
Алгоритмы на языке С++
(поиск с перемещением и транспозицией)
Описанные выше методы оптимизации поиска для односвязного списка, полем данных которого будут целые числа, на языке С++ можно реализовать следующими функциями:
/* Функция поиска элемента в списке с перестановкой найденного элемента в начало списка */
PNode Find1(PNode& First, int KEY)
{
PNode search=0;
PNode q=NULL;
PNode p=First;
while (p)
{
if (KEY==p->Data)
{
search=p;
if (!q)
{
return 0;
}
q->Next=p->Next;
p->Next=First;
First=p;
return 0;
}
q=p;
p=p->Next;
}
search =0;
return search ;
}
/------------------------------------------------------------------------------------/
/* Функция поиска элемента в списке с транспозицией */
PNode Find2(PNode& First, int KEY)
{
PNode search=0;
PNode S=0;
PNode q=0;
PNode p=First;
while (p)
{
if (KEY==p->Data)
{
if (!q)
{
return 0;
}
q->Next=p->Next;
p->Next=q;
if (!S) First=p;
else
{
S->Next=p;
search=p;
}
return search;
}
S=q;
q=p;
p=p->Next;
}
search=0;
return search;
}
/------------------------------------------------------------------------------------/
Задания
Дан массив целых чисел. Решить заданную согласно варианту задачу и переставить найденный элемент обоими методами оптимизации поиска в начало списка.
1. Найти максимальный элемент массива.
2. Найти минимальный элемент массива.
3. Найти значение lg (x) от каждого элемента и переставить на 1 место элемент, значение функции от которого максимально.
4. Найти число, нацело делящееся на 11 (если таких чисел несколько, то найти максимальное; если таких чисел нет - выдать сообщение).
5. Найти элемент, разность соседних элементов которого не меньше 72. Если таких элементов несколько, выбрать максимальный. Если таких элементов нет, выдать сообщение.
6. Найти элемент, частное соседних элементов которого четное число. Если таких элементов несколько, выбрать максимальный или минимальный элемент. Если таких элементов нет, выдать сообщение.
7. Найти элемент, разность соседних элементов которого четное число. Если таких элементов несколько, выбрать максимальный или минимальный элемент. Если такого элемента нет, выдать сообщение.
8. Найти элемент, среднее арифметическое элементов, находящихся до этого элемента равно 12. Если таких элементов нет, выдать сообщение.
9. Найти максимальный элемент, делящийся на 10. Если такого элемента нет, выдать сообщение.
10. Найти элемент, разность соседних элементов которого четное число и делится на 3. Если такого элемента нет, выдать сообщение.
11. Найти элемент, для среднее квадратичное элементов, находящихся после этого элемента меньше 10. Если таких элементов несколько, выбрать максимальный элемент. Если таких элементов нет, выдать сообщение.
12. Найти значение tg (x) от каждого элемента и переставить на 1 место элемент, значение функции от которого максимально.
Дата: 2019-12-10, просмотров: 458.