Для вставки элемента в дерево, сначало нужно осуществить поиск в дереве по заданному ключу. Если такой ключ имеется, то программа завершается, если нет, то происходит вставка.
Для включения новой записи в дерево, прежде всего, нужно найти тот узел, к которому можно присоединить новый элемент, не нарушив упорядоченности дерева. Алгоритм поиска нужного узла тот же самый, что и при поиске узла с заданным ключом. Однако непосредственно использовать функцию поиска нельзя, потому что по ее окончании она не фиксирует ссылку на узел, после которго поиск прекращается.
Модифицируем функцию поиска так, чтобы фиксировалась ссылка на узел, в котором был найден заданный ключ (в случае успешного поиска), или ссылка на узел, после обработки которого поиск прекращается (в случае неуспешного поиска).
Модифицированный алгоритм следующий:
p = tree
q = nil
while p <> nil do
q = p
if key = k(p) then
search = p
return
endif
if key < k(p) then
p = left(p)
else
p = right(p)
endif
endwhile
v = maketree(key, rec)
if q = nil then
tree = v
else
if key < k(q) then
left(q) = v
else
right(q) = v
endif
endif
search = v
return
Поиск с удалением
Удаление узла не должно нарушить упорядоченности дерева. Возможны три варианта:
1) Найденный узел является листом. Тогда он просто удаляется с прмощью обычной операции удаления.
2) Найденный узел имеет только одного сына. Тогда сын перемещается на место отца.
3) У удаляемого узла два сына. В этом случае нужно найти подходящее звено поддерева, которое можно было бы вставить на место удаляемого. Такое звено всегда существует. На место отца помещается либо его предшественник при обходе слева направо, либо его преемник при том же виде обхода.
Предшественник - это самый правый элемент левого поддерева (для достижения этого элемента необходимо перейти в следующий узел по левой ветви, а затем двигаться только по правой ветви этого узла до тех пор, пока очередная ссылка не будет равна nil).
Преемник - это самый левый элемент правого поддерева (для достижения этого элемента необходимо перейти в следующий узел по правой ветви, а затем двигаться только по левой ветви этого узла до тех пор, пока очередная ссылка не будет равна nil).
Предшественником удаляемого узла 12 в дереве на рис. 5.9 будет узел 11 (самый правый узел левого поддерева). Преемником – узел 13 (самый левый узел правого поддерева).
Будем разрабатывать алгоритм для преемника (рис.5.9).
p - рабочий указатель;
q - отстает от р на один шаг;
v - указывает на приемника удаляемого узла;
t - отстает от v на один шаг;
s - на один шаг впереди v (указывает на левого сына или пустое место).
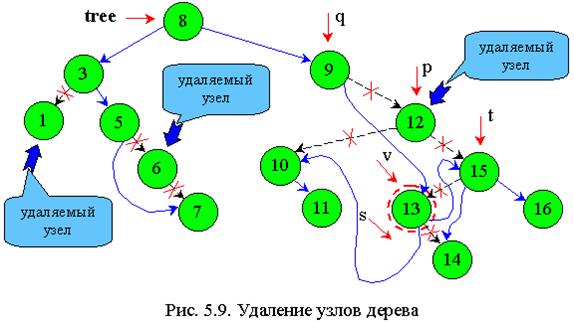
На узел 13 в результате поиска приемника должен указывать указатель v, а указатель s - на пустое место (как показано на рис. 5.9).
Алгоритм поиска по бинарному дереву с удалением:
q = nil
p = tree
while (p <> nil) and (k(p) <> key) do
q = p
if key < k(p) then
p = left(p)
else
p = right(p)
endif
endwhile
if p = nil then ‘Ключ не найден’
return
endif
if left(p) = nil then v = right(p)
else if right(p) = nil
then v = left(p)
else
‘У nod(p) - два сына’
‘Введем два указателя (t отстает от v на 1 шаг, s - опережает)’
t = p
v = right(p)
s = left(v)
while s <> nil do
t = v
v = s
s = left(v)
endwhile
if t <> p then
‘v не является сыном p’
left(t) = right(v)
right(v) = right(p)
endif
left(v) = left(p)
endif
endif
if q = nil then ‘p - корень’
tree = v
else if p = left(q)
then left(q) = v
else right(q) = v
endif
endif
freenode(p)
return
Контрольные вопросы
1. В чем состоит назначение поиска?
2. Что такое уникальный ключ?
3. Какая операция производится в случае отсутствия заданного ключа в списке?
4. В чем разница между последовательным и индексно-последовательным поиском?
5. Какой из них более эффективный и почему?
6. Какие способы переупорядочивания таблицы вы знаете?
7. Основные отличия метода перестановки в начало от метода транспозиции?
8. Где они будут работать быстрее, в массиве или списке?
9. В каких списках они работают, упорядоченных или нет?
10. В чем суть бинарного поиска?
11. Как можно обойти бинарное дерево?
12. Можно ли применять бинарный поиск к массивам?
13. Если удалить корень в непустом бинарном дереве, какой элемент станет на его место?
Сортировка
При обработке данных важно знать информационное поле данных и размещение их в машине.
Сортировка - это расположение данных в памяти в регулярном виде по выбранному параметру. Регулярность рассматривают как возрастание (убывание) значения параметра от начала к концу в массиве.
Различают внутреннюю и внешнюю сортировку:
- внутренняя сортировка - сортировка в оперативной памяти;
- внешняя сортировка - сортировка во внешней памяти.
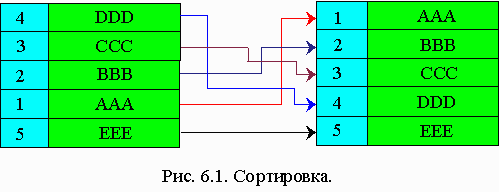
Если сортируемые записи занимают большой объем памяти, то их перемещение требует больших затрат. Для того, чтобы их уменьшить, сортировку производят в таблице адресов ключей, делают перестановку указателей, т.е. сам массив не перемещается. Это метод сортировки таблицы адресов.
При сортировке могут встретиться одинаковые ключи. В этом случае при сортировке желательно расположить после сортировки одинаковые ключи в том же порядке, что и в исходном файле. Это - устойчивая сортировка.
Эффективность сортировки можно рассматривать по нескольким критериям:
время, затрачиваемое на сортировку;
объем оперативной памяти, требуемой для сортировки;
время, затраченное программистом на написание программы.
Выделяем первый критерий, поскольку мы будем рассматривать только методы сортировки «на том же месте», то есть не использующие для процесса сортировки дополнительную оперативную память. Эквивалентом затраченного на сортировку времени можно считать количество сравнений при выполнении сортировки и количество перемещений.
Порядок числа сравнения при сортировке лежит в пределах от O(n log n) до O(n2).
О(n) - идеальный и недостижимый случай.
Различают следующие методы сортировки:
строгие (прямые) методы;
улучшенные методы.
Строгие методы:
1) метод прямого включения;
2) метод прямого выбора;
3) метод прямого обмена.
Эффективность трех строгих методов примерно одинакова.
Дата: 2019-12-10, просмотров: 403.