Пусть заданы элементы с ключами: 14, 18, 6, 21, 1, 13, 15. После выполнения нижеприведенного алгоритма получится дерево, изображенное на рис.4.6. Если обойти полученное дерево слева направо, то получим упорядочивание: 1, 6, 13, 14, 15, 18, 21.
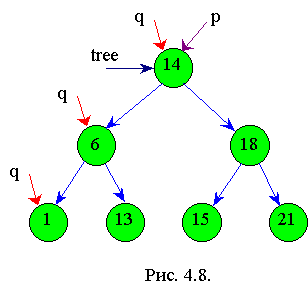
Алгоритм создания бинарного дерева:
read ( key , rec )
tree = maketree(key, rec)
while not eof do
p = tree
q = tree
read (key, rec)
v = maketree(key, rec)
while p <> nil do
q = p
if key < k(p) then
p = left(p)
else
p = right(p)
endif
endwhile
if key < k(q) then
left(q) = v
else
right(q) = v
endif
endwhile
return
4.2.4 Прохождение (обход) бинарных деревьев
В зависимости от последовательности обхода узлов различают три вида обхода (прохождения) деревьев (рис.4.9):
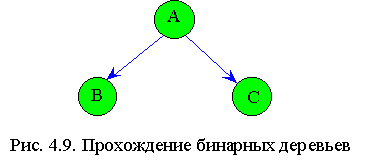
1. Сверху вниз А, В, С.
2. Слева направо или симметричное прохождение В, А, С.
3. Снизу вверх В, С, А.
Наиболее часто применяется второй способ.
Ниже приведены рекурсивные алгоритмы прохождения бинарных деревьев.
| subroutine pretrave (tree) ‘ сверху вниз ’ if tree <> nil then print info(tree) pretrave(left(tree)) pretrave(right(tree)) endif return subroutine intrave (tree) ‘симметричный или слева направо’ if tree <> nil then intrave(left(tree)) print info(tree) intrave(right(tree)) endif return subrotine postrave (tree) ‘ снизу вверх ’ if tree<>nil then postrave (left(tree)) postrave (right(tree)) print info(tree) endif return |
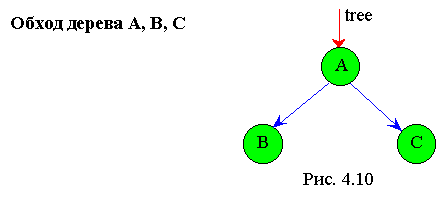
Поясним подробнее рекурсию алгоритма обхода дерева слева направо.
Пронумеруем строки алгоритма intrave ( tree ):
1 if tree <> nil
2 then intrave (left(tree))
3 print info (tree)
4 intrave (right (tree))
5 endif
6 return
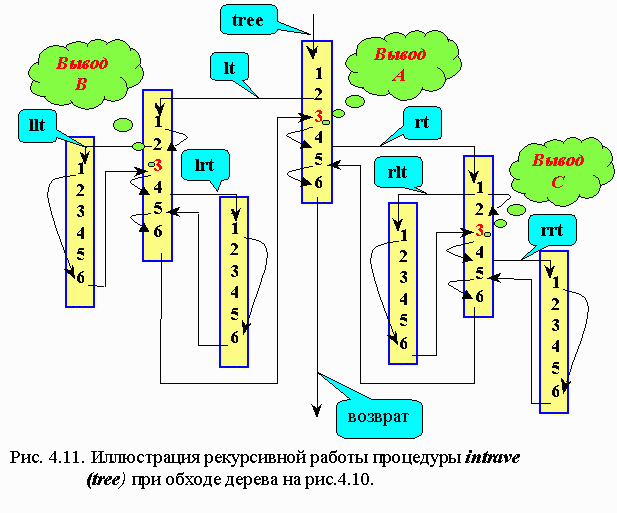
Обозначим указатели: t → tree; l → left; r → right
На приведенном рис. 4.11 проиллюстрирована последовательность вызова функции intrave ( tree) по мере обхода узлов простейшего дерева, изображенного на рис. 4. 10.
Поиск
Поиск является одной из основных операций при обработке информации в ЭВМ. Ее назначение - по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу.
Набор данных (любых) будем называть таблицей или файлом. Любое данное (или элемент структуры) отличается каким-то признаком от других данных. Этот признак называется ключом. Ключ может быть уникальным, т. е. в таблице существует только одно данное с этим ключом. Такой уникальный ключ называется первичным. Вторичный ключ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных могут быть собраны в одном месте (в другой таблице) или представлять собой запись, в которой одно из полей - это ключ. Ключи, которые выделены из таблицы данных и организованы в свой файл, называются внешними ключами. Если ключ находится в записи, которую он определяет, то он называется внутренним.
Поиском по заданному аргументу называется алгоритм, определяющий соответствие ключа заданному аргументу. Результатом работы алгоритма поиска может быть нахождение этого ключа или отсутствие его в таблице. В случае отсутствия ключа (и информации, ему соответствующей) возможны две операции:
индикация того, что ключа нет;
вставка ключа (и информации) в таблицу.
В случае нахождения ключа (и информации ему соответствующей) возможны две операции:
обработка найденной информации;
удаление найденной информации.
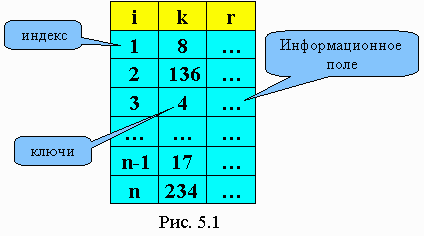
Пусть k - массив ключей. Для каждого k(i) существует r(i) - данное. Key - аргумент поиска. Ему соответствует информационная запись rec. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.
Последовательный поиск
Применяется в том случае, если неизвестна организация данных или данные неупорядочены. Тогда производится последовательный просмотр по всей таблице начиная от младшего адреса в оперативной памяти и кончая самым старшим.
Ниже представлен алгоритм последовательного поиска в массиве (переменная search хранит номер найденного элемента).
for i = 1 to n
if k(i) = key then
search = i
return
endif
next i
search = 0
return
Если элемент не найден в таблице и необходимо произвести вставку, то последние 2 оператора заменяются на
n = n + 1
k(n) = key
r(n) = rec
search = n
return
Если таблица данных задана в виде односвязного списка, то производится последовательный поиск в списке (рис. 5.2).
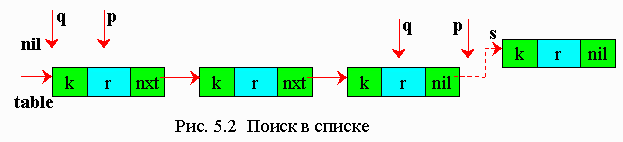
Ниже представлен алгоритм последовательного поиска в списке.
q = nil
p = table
while (p <> nil) do
if k(p) = key then
search = p
return
endif
q = p
p = nxt(p)
endwhile
s = getnode
k(s) = key
r(s) = rec
nxt(s) = nil
if q = nil then
table = s
else
nxt(q) = s
endif
search = s
return
Достоинством списковой структуры является ускоренный алгоритм удаления или вставки элемента в список, причем время вставки или удаления не зависит от количества элементов, а в массиве каждая вставка или удаление требуют передвижения примерно половины элементов. Эффективность поиска в списке примерно такая же, как и в массиве.
Эффективность любого поиска может оцениваться по количеству сравнений C аргумента поиска с ключами таблицы данных. Чем меньше количество сравнений, тем эффективнее алгоритм поиска.
Эффективность последовательного поиска в массиве
C min = 1, C max = n.
Если данные расположены равновероятно во всех ячейках массива, то
C ср ≈ (n + 1)/2.
Эффективность последовательного поиска в списке - то же самое.
Порядок эффективности последовательного поиска O(n) (величина одного порядка с n).
Эффективность последовательного поиска можно увеличить.
Дата: 2019-12-10, просмотров: 401.