Эффективность любого поиска может оцениваться по количеству сравнений C аргумента поиска с ключами таблицы данных. Чем меньше количество сравнений, тем эффективнее алгоритм поиска.

Эффективность последовательного поиска в массиве:

C = 1  n , C = ( n + 1)/2.

Эффективность последовательного поиска в списке - то же самое. Хотя по количеству сравнений поиск в списке и в массиве имеет одинаковую эффективность, организация данных в виде массива и списка имеет свои достоинства и недостатки. Целью поиска является выполнение следующих операций:

1) Найденную запись считать.

2) При отсутствии записи произвести ее вставку в таблицу.

3) Найденную запись удалить.

Первая операция (собственно поиск) занимает для них одно время. Вторая и третья операции для списочной структуры более эффективна (т. к. у массивов надо сдвигать элементы).

Если k - число передвижений элементов в массиве, то k = (n + 1)/2.

5.4 Эффективность индексно-последовательного поиска

Если считать равновероятным появление всех случаев, то эффективность поиска можно рассчитать следующим образом:

Введем обозначения: 

n – размер основной таблицы;

m - размер индексной таблицы; 

p - размер шага;

m = n / p;

Тогда количество сравнений C считается так:

С = ( m +1)/2 + ( p +1)/2 = ( n / p +1)/2 + ( p +1)/2 = n /2 p + p /2+1

Продифференцируем C по p и приравняем производную нулю:

dC/dp=(d/dp) (n/2p+p/2+1)= - n /2 p² + 1/2 = 0

Отсюда

p ² = n ;

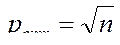
Подставив р_опт в выражение для C, получим следующее количество сравнений:

C = 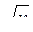 +1

Порядок эффективности индексно-последовательного поиска O ( ).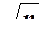

Методы оптимизации поиска

Всегда можно говорить о некотором значении вероятности поиска того или иного элемента в таблице. Считаем, что в таблице данный элемент существует. Тогда вся таблица поиска может быть представлена как система с дискретными состояниями, а вероятность нахождения там искомого элемента - это вероятность p(i) i - го состояния системы.

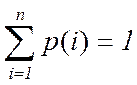
 Количество сравнений при поиске в таблице, представленной как дискретная система, представляет собой математическое ожидание значения дискретной случайной величины, определяемой вероятностями состояний и номерами состояний системы.

Z = C =1 p (1)+2 p (2)+3 p (3)+…+ np ( n )

Желательно, чтобы p(1)  p(2)  p(3)  …  p(n).

Это минимизирует количество сравнений, то есть увеличивает эффективность. Так как последовательный поиск начинается с первого элемента, то на это место надо поставить элемент, к которому чаще всего обращаются (с наибольшей вероятностью поиска).

Наиболее часто используются два основных способа автономного переупорядочивания таблиц поиска. Рассмотрим их на примере односвязных списков.