Вариант № 1.
Решить:
1. 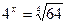 2.
2. 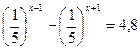 3.
3. 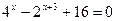 4.
4. 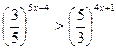 5.
5. 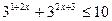
| Вариант № 2.
Решить:
1. 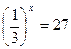 2.
2. 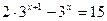 3.
3. 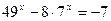 4.
4. 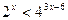 5.
5. 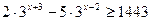
| Вариант № 3.
Решить:
1. 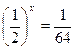 2.
2. 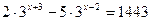 3.
3. 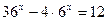 4.
4. 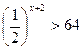 5.
5. 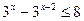
|
Вариант № 4.
Решить:
1. 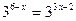 2.
2. 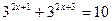 3.
3. 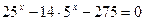 4.
4. 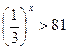 5.
5. 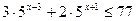
| Вариант № 5.
Решить:
1. 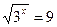 2.
2. 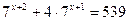 3.
3. 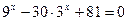 4.
4. 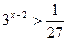 5.
5. 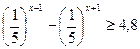
| Вариант № 6.
Решить:
1. 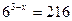 2.
2. 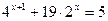 3.
3. 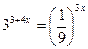 4.
4. 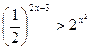 5.
5. 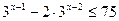
|
Вариант № 7.
Решить:
1. 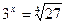 2.
2. 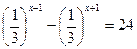 3.
3. 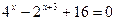 4.
4. 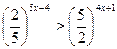 5.
5. 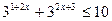
| Вариант № 8.
Решить:
1. 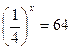 2.
2. 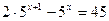 3.
3. 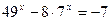 4.
4. 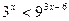 5.
5. 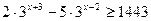
| Вариант № 9.
Решить:
1. 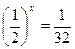 2.
2. 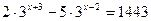 3.
3. 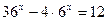 4.
4. 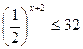 5.
5. 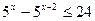
|
Вариант № 10.
Решить:
1. 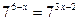 2.
2. 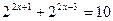 3.
3. 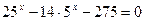 4.
4. 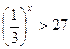 5.
5. 
| Вариант № 11.
Решить:
1. 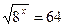 2.
2. 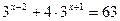 3.
3. 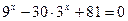 4.
4. 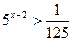 5.
5. 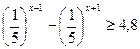
| Вариант № 12.
Решить:
1. 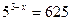 2.
2. 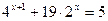 3.
3. 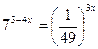 4.
4. 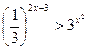 5.
5. 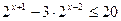
|
Вариант №13.
Решить:
1. 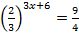 2.
2. 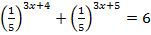 3.
3. 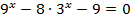 4.
4. 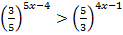 5.
5. 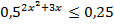
| Вариант №14.
Решить:
1. 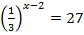 2.
2. 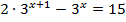 3.
3. 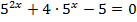 4.
4. 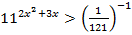 5.
5. 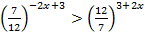
| Вариант №15.
Решить:
1. 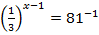 2.
2. 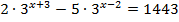 3.
3. 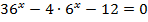 4.
4. 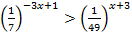 5.
5. 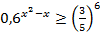
|
Вариант №16.
Решить:
1. 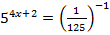 2.
2. 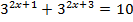 3.
3. 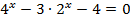 4.
4. 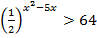 5.
5. 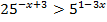
| Вариант №17.
Решить:
1. 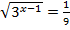 2.
2. 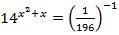 3.
3. 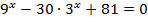 4.
4. 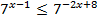 5.
5. 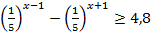
| Вариант №18.
Решить:
1. 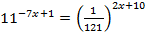 2.
2. 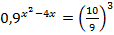 3.
3. 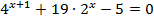 4.
4. 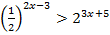 5.
5. 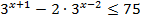
|
Вариант №19.
Решить:
1. 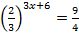 2.
2. 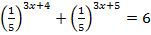 3.
3. 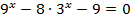 4.
4. 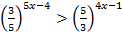 5.
5. 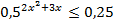
| Вариант №20.
Решить:
1. 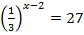 2.
2. 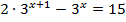 3.
3. 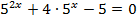 4.
4. 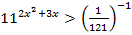 5.
5. 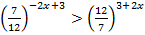
| Вариант №21.
Решить:
1. 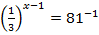 2.
2. 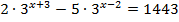 3.
3. 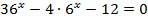 4.
4. 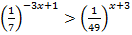 5.
5. 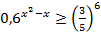
|
Вариант №22.
Решить:
1. 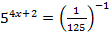 2.
2. 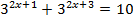 3.
3. 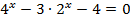 4.
4. 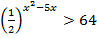 5.
5. 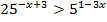
| Вариант №23.
Решить:
1. 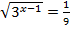 2.
2. 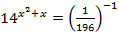 3.
3. 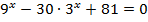 4.
4. 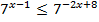 5.
5. 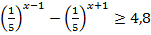
| Вариант №24.
Решить:
1. 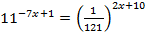 2.
2. 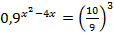 3.
3. 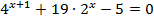 4.
4. 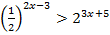 5.
5. 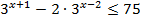
|
Вариант №25.
Решить:
1. 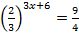 2.
2. 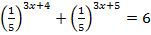 3.
3. 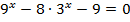 4.
4. 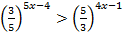 5.
5. 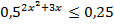
| Вариант №26.
Решить:
1. 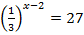 2.
2. 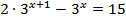 3.
3. 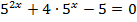 4.
4. 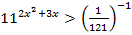 5.
5. 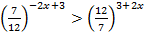
| Вариант №27.
Решить:
1. 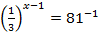 2.
2. 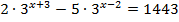 3.
3. 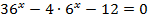 4.
4. 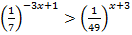 5.
5. 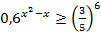
|
Вариант №28.
Решить:
1. 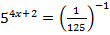 2.
2. 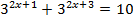 3.
3. 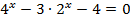 4.
4. 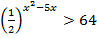 5.
5. 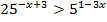
| Вариант №29.
Решить:
1. 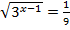 2.
2. 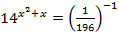 3.
3. 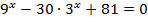 4.
4. 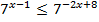 5.
5. 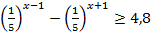
| Вариант №30.
Решить:
1. 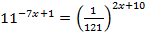 2.
2. 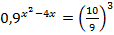 3.
3. 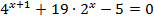 4.
4. 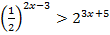 5.
5. 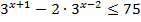
|
Логарифмические уравнения и неравенства
Вариант № 1.
Решить:
1. 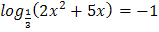 2.
2. 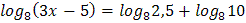 3.
3. 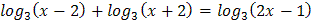 4.
4. 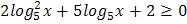 5.
5. 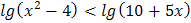
| Вариант № 2.
Решить:
1. 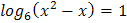 2.
2. 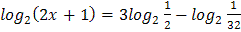 3.
3. 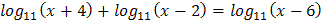 4.
4. 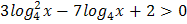 5.
5. 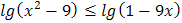
|
Вариант № 3.
Решить:
1. 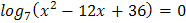 2.
2. 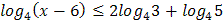 3.
3. 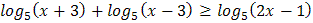 4.
4. 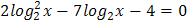 5.
5. 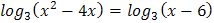
| Вариант № 4.
Решить:
1. 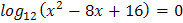 2.
2. 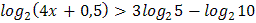 3.
3. 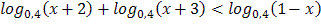 4.
4. 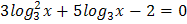 5.
5. 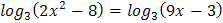
|
Вариант № 5.
Решить:
1. 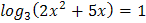 2.
2. 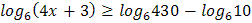 3.
3. 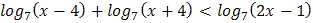 4.
4. 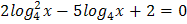 5.
5. 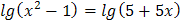
| Вариант № 6.
Решить:
1. 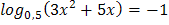 2.
2. 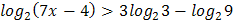 3.
3. 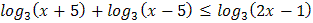 4.
4. 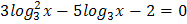 5.
5. 
|
Вариант № 7.
Решить:
1. 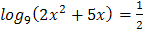 2.
2. 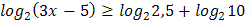 3.
3. 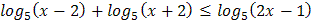 4.
4. 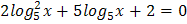 5.
5. 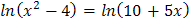
| Вариант № 8.
Решить:
1. 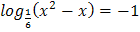 2.
2. 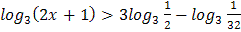 3.
3. 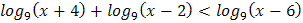 4.
4. 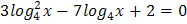 5.
5. 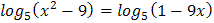
|
Вариант № 9.
Решить:
1. 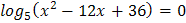 2.
2. 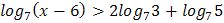 3.
3. 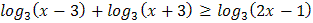 4.
4. 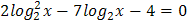 5.
5. 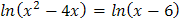
| Вариант № 10.
Решить:
1. 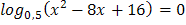 2.
2. 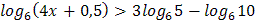 3.
3. 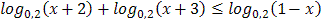 4.
4. 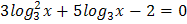 5.
5. 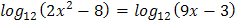
|
Вариант № 11.
Решить:
1. 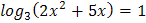 2.
2. 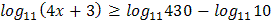 3.
3. 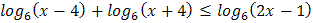 4.
4. 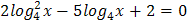 5.
5. 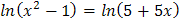
| Вариант № 12.
Решить:
1. 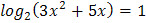 2.
2. 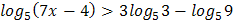 3.
3. 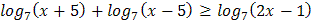 4.
4. 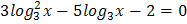 5.
5. 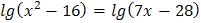
|
Вариант № 13.
Решить:
1. 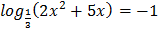 2.
2. 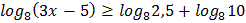 3.
3. 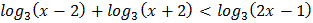 4.
4. 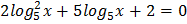 5.
5. 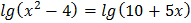
|
Вариант № 14.
Решить:
1. 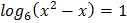 2.
2. 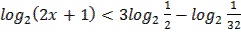 3.
3. 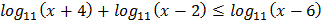 4.
4. 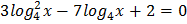 5.
5. 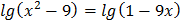
|
Вариант № 15.
Решить:
1. 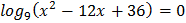 2.
2. 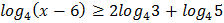 3.
3. 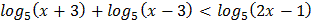 4.
4. 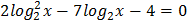 5.
5. 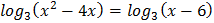
|
Вариант № 16.
Решить:
1. 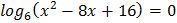 2.
2. 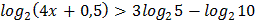 3.
3. 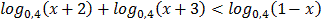 4.
4. 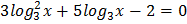 5.
5. 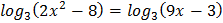
|
Вариант № 17.
Решить:
1. 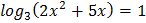 2.
2. 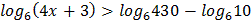 3.
3. 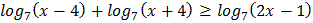 4.
4. 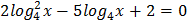 5.
5. 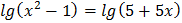
| Вариант № 18.
Решить:
1. 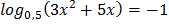 2.
2. 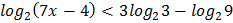 3.
3. 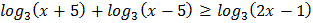 4.
4. 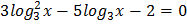 5.
5. 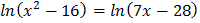
|
Вариант № 19.
Решить:
1. 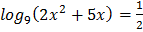 2.
2. 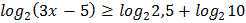 3.
3. 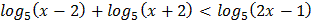 4.
4. 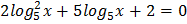 5.
5. 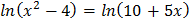
| Вариант № 20.
Решить:
1. 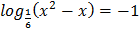 2.
2. 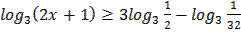 3.
3. 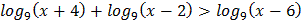 4.
4. 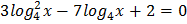 5.
5. 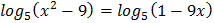
|
Вариант № 21.
Решить:
1. 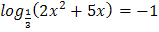 2.
2. 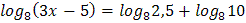 3.
3. 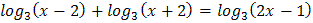 4.
4. 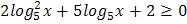 5.
5. 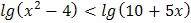
| Вариант № 22.
Решить:
1. 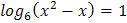 2.
2. 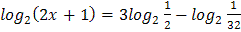 3.
3. 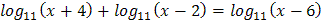 4.
4. 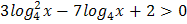 5.
5. 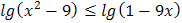
|
Вариант № 23.
Решить:
1. 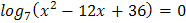 2.
2. 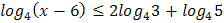 3.
3. 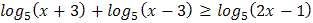 4.
4. 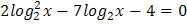 5.
5. 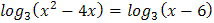
| Вариант № 24.
Решить:
1. 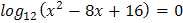 2.
2. 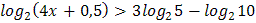 3.
3. 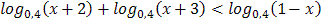 4.
4. 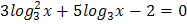 5.
5. 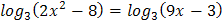
|
Вариант № 25.
Решить:
1. 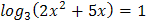 2.
2. 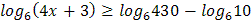 3.
3. 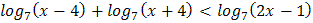 4.
4. 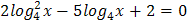 5.
5. 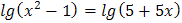
| Вариант № 26.
Решить:
1. 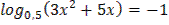 2.
2. 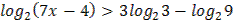 3.
3. 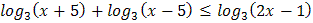 4.
4. 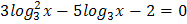 5.
5. 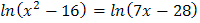
|
Вариант № 27.
Решить:
1. 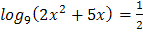 2.
2. 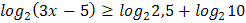 3.
3. 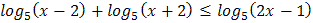 4.
4. 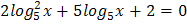 5.
5. 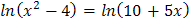
| Вариант № 28.
Решить:
1. 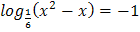 2.
2. 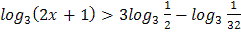 3.
3. 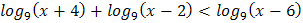 4.
4. 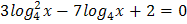 5.
5. 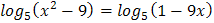
|
Вариант № 29.
Решить:
1. 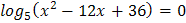 2.
2. 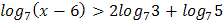 3.
3. 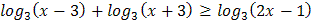 4.
4. 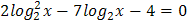 5.
5. 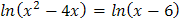
| Вариант № 30.
Решить:
1. 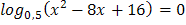 2.
2. 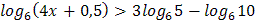 3.
3. 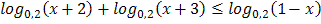 4.
4. 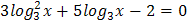 5.
5. 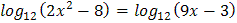
|
Тригонометрические уравнения
Вариант №1.
Решить уравнения:
1. 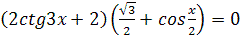 2.
2. 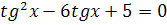 3.
3. 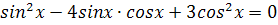
|
Вариант №2.
Решить уравнения:
1. 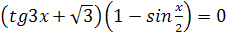 2.
2. 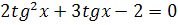 3.
3. 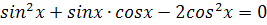
|
Вариант №3.
Решить уравнения:
1. 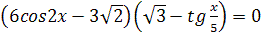 2.
2.  3.
3. 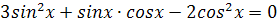
|
Вариант №4.
Решить уравнения:
1. 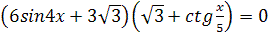 2.
2. 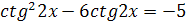 3.
3. 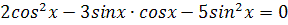
|
Вариант №5.
Решить уравнения:
1. 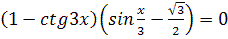 2.
2. 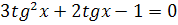 3.
3. 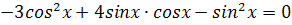
| Вариант № 6 .
Решить уравнения:
1. 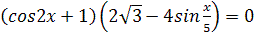 2. 8
2. 8 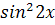 +cos2x+1=0
3. +cos2x+1=0
3. 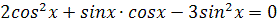
|
Вариант № 7 .
Решить уравнения:
1. 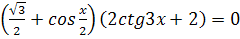 2.
2. 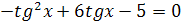 3.
3. 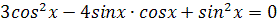
| Вариант № 8 .
Решить уравнения:
1. 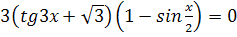 2.
2. 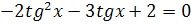 3.
3. 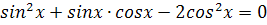
|
Вариант № 9 .
Решить уравнения:
1. 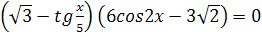 2.
2. 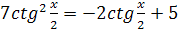 3.
3. 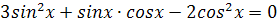
| Вариант № 10 .
Решить уравнения:
1. 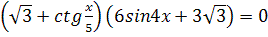 2.
2. 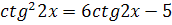 3.
3. 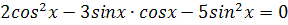
|
Вариант № 11 .
Решить уравнения:
1. 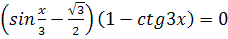 2.
2. 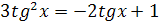 3.
3. 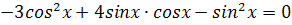
| Вариант № 12 .
Решить уравнения:
1. 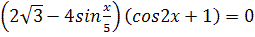 2. 8
2. 8 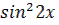 = - cos 2x - 1
3. = - cos 2x - 1
3. 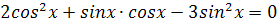
|
Вариант №1 3 .
Решить уравнения:
1. 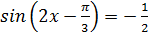 2.
2. 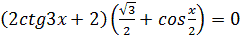 3.
3. 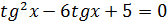
| Вариант № 14 .
Решить уравнения:
1. 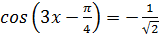 2.
2. 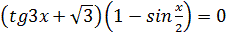 3.
3. 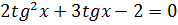
|
Вариант № 15 .
Решить уравнения:
1. 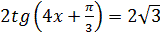 2.
2. 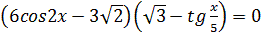 3.
3. 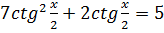
| Вариант № 16 .
Решить уравнения:
1. 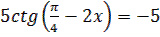 2.
2. 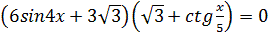 3.
3. 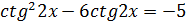
|
Вариант № 17 .
Решить уравнения:
1. 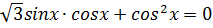 2.
2. 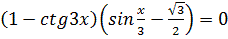 3.
3. 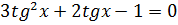
| Вариант № 18 .
Решить уравнения:
1. 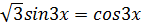 2.
2. 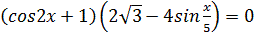 3. 8
3. 8 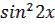 +cos2x+1=0 +cos2x+1=0
|
Вариант № 19 .
Решить уравнения:
1. 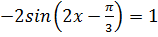 2.
2. 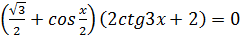 3.
3. 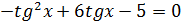
| Вариант № 20 .
Решить уравнения:
1. 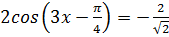 2.
2. 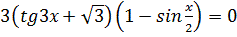 3.
3. 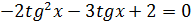
|
Вариант № 21 .
Решить уравнения:
1. 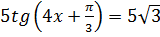 2.
2. 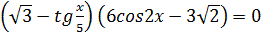 3.
3. 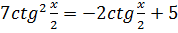
| Вариант № 22.
Решить уравнения:
1. 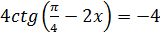 2.
2. 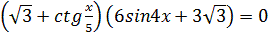 3.
3. 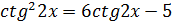
|
Вариант № 23 .
Решить уравнения:
1. 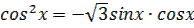 2.
2. 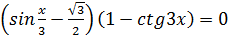 3.
3. 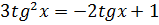
| Вариант № 24 .
Решить уравнения:
1. 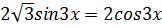 2.
2. 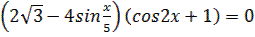 3. 8
3. 8 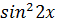 = - cos 2x - 1 = - cos 2x - 1
|
Вариант № 25 .
Решить уравнения:
1. 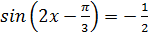 2.
2. 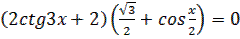 3.
3. 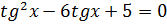
| Вариант № 26 .
Решить уравнения:
1. 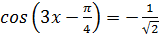 2.
2. 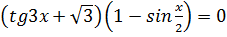 3.
3. 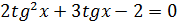
|
Вариант № 27 .
Решить уравнения:
1. 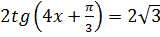 2.
2. 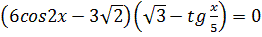 3.
3. 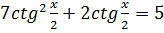
| Вариант № 28 .
Решить уравнения:
1. 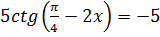 2.
2. 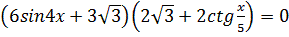 3. 3. 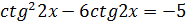
|
Вариант № 29 .
Решить уравнения:
1. 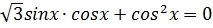 2.
2. 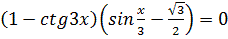 3.
3. 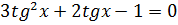
| Вариант № 30 .
Решить уравнения:
1. 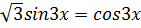 2.
2. 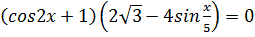 3. 8
3. 8 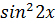 +cos2x+1=0 +cos2x+1=0
|
Приложение производной
3.1 Найти производные функций:
Вариант №1.
Найти производные функций :
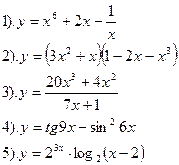
| Вариант №2.
Найти производные функций :
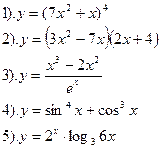
| Вариант №3.
Найти производные функций :
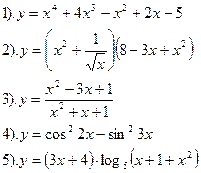
|
Вариант №4.
Найти производные функций :
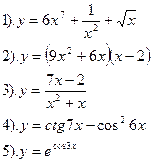
| Вариант №5.
Найти производные функций :
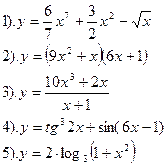
| Вариант №6.
Найти производные функций :
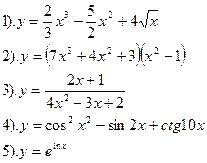
|
Вариант №7.
Найти производные функций :
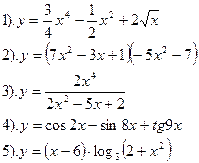
| Вариант №8.
Найти производные функций :
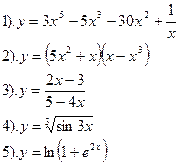
| Вариант №9.
Найти производные функций :
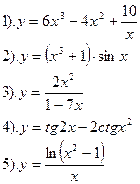
|
Вариант №10.
Найти производные функций :
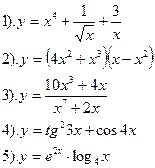
| Вариант №11.
Найти производные функций :
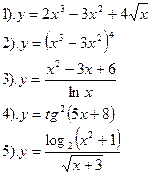
| Вариант №12.
Найти производные функций :
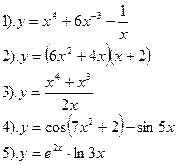
|
Вариант №13.
Найти производные функций:
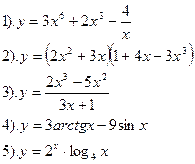
| Вариант №14.
Найти производные функций:
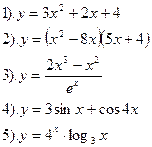
| Вариант №15.
Найти производные функций:
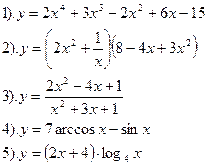
|
Вариант №16.
Найти производные функций:
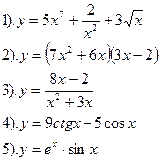
| Вариант №17.
Найти производные функций:

| Вариант №18.
Найти производные функций:
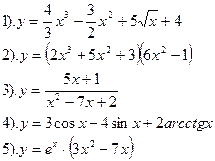
|
Вариант №19.
Найти производные функций:
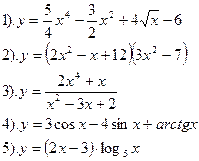
| Вариант №20.
Найти производные функций:
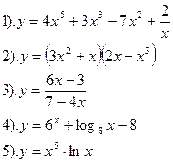
| Вариант №21.
Найти производные функций:
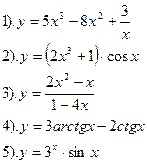
|
Вариант №22.
Найти производные функций:
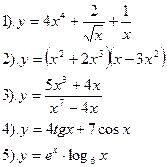
| Вариант №23.
Найти производные функций:
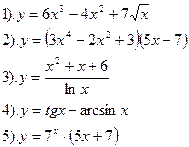
| Вариант №24.
Найти производные функций:
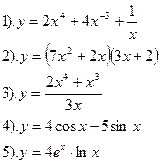
|
Вариант №25.
Найти производные функций:
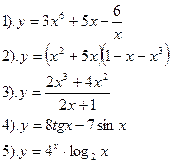
| Вариант №26.
Найти производные функций:
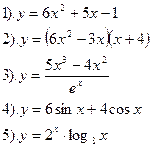
| Вариант №27.
Найти производные функций:
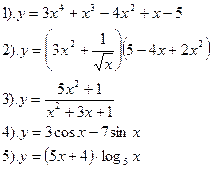
|
Вариант №28.
Найти производные функций:
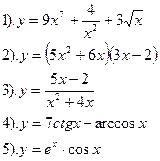
| Вариант №29.
Найти производные функций:
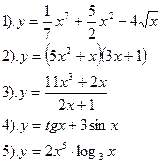
| Вариант №30.
Найти производные функций:
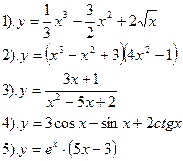
|
Неопределённый интеграл
Вариант №1.
Найти:
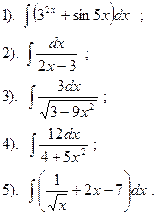
| Вариант №2.
Найти:
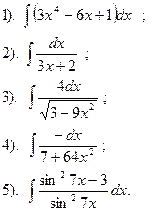
| Вариант №3.
Найти:
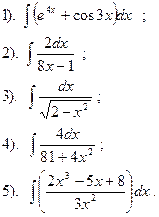
| Вариант №4.
Найти:
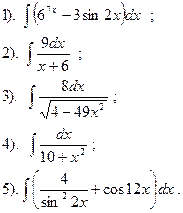
|
Вариант №5.
Найти:
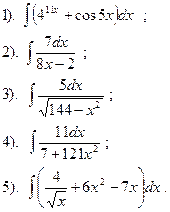
| Вариант №6.
Найти:
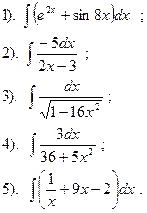
| Вариант №7.
Найти:
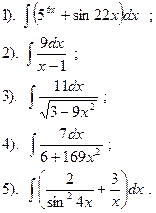
| Вариант №8.
Найти:
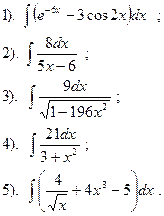
|
Вариант №9.
Найти:
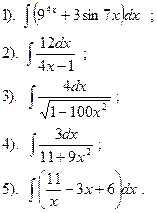
| Вариант №10.
Найти:
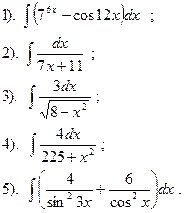
| Вариант №11.
Найти:
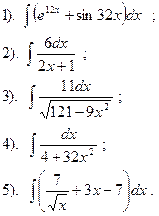
| Вариант №12.
Найти:
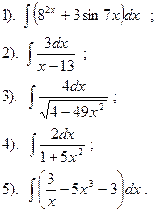
|
Вариант №13.
Найти:
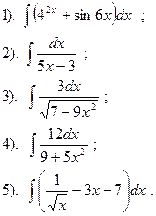
|
Вариант №14.
Найти:
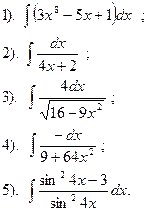
|
Вариант №15.
Найти:
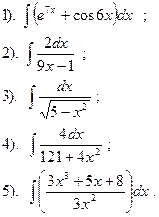
|
Вариант №16.
Найти:
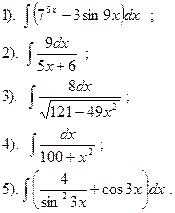
|
Вариант №17.
Найти:
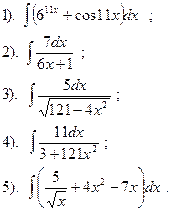
|
Вариант №18.
Найти:
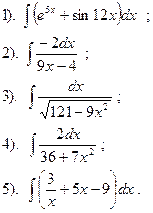
|
Вариант №19.
Найти:
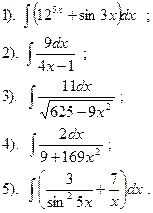
|
Вариант №20.
Найти:
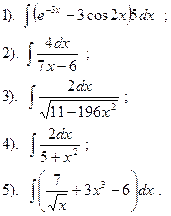
|
Вариант №21.
Найти:
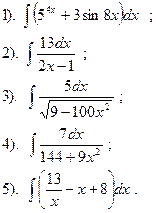
|
Вариант №22.
Найти:
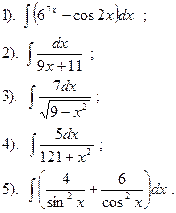
|
Вариант №23.
Найти:
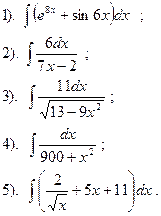
|
Вариант №24.
Найти:
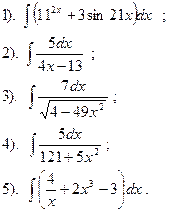
|
Вариант №25.
Найти:
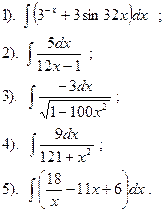
|
Вариант №26.
Найти:
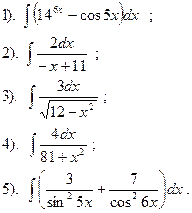
|
Вариант №27.
Найти:
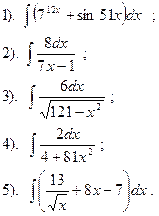
|
Вариант №28.
Найти:
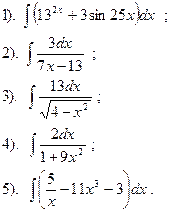
|
Вариант №29.
Найти:
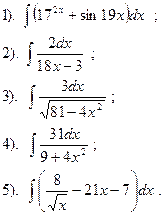
| Вариант №30.
Найти:
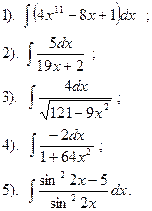
|
Определённый интеграл
Построить схематически чертёж и найти площадь фигуры, ограниченной линиями:
1. 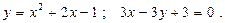
2. 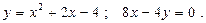
3. 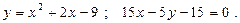
4. 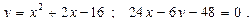
5. 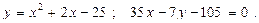
6. 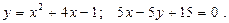
7. 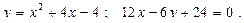
8. 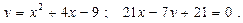
9. 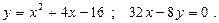
10. 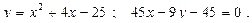
11. 
12. 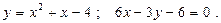
13. 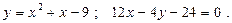
14. 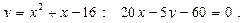
15. 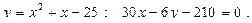
16. 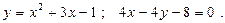
17. 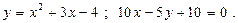
18. 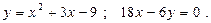
19. 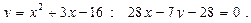
20. 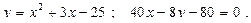
21. 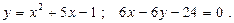
22. 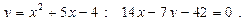
23. 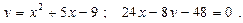
24. 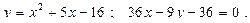
25. 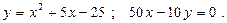
26. 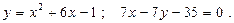
27. 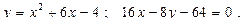
28. 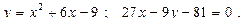
29. 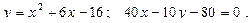
30. 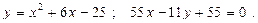
Геометрия
Вариант №1.
1. Шар с центром в точке О касается плоскости в точке А. Точка В лежит в плоскости касания. Найдите объём шара, если АВ=21 см, ВО=29 см.


2. В правильной треугольной призме АВСА1В1С1 проведено сечение через вершину С1 и ребро АВ. Найдите периметр сечения, если сторона основания равна 24см, а боковое ребро -10см.
Вариант №2.
1. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
2. В прямоугольном параллелепипеде стороны основания равны 5см и 12см, а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
Вариант № 3.
1. Образующая конуса равна 25см, а радиус основания-7см. Найдите его объём.
2. В правильной четырёхугольной пирамиде высота равна 12см, а апофема-15см. Найдите боковое ребро пирамиды.
Вариант № 4.
1. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
2. В правильной четырёхугольной пирамиде высота равна 7см, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды.
Вариант № 5.
1. Радиус основания цилиндра равен 5см, а его образующая-9см. Найдите площадь осевого сечения.
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота-12см. Найдите площадь полной поверхности пирамиды.
Вариант № 6.
1. Радиус основания конуса равен 14см. Найдите площадь сечения, проведённого перпендикулярно его оси через её середину.
2. В основании прямого параллелепипеда лежит ромб, диагонали которого равны 12см и 16см. Высота параллелепипеда-8см. Найдите площадь его полной поверхности.
Вариант № 7.
1. Сферу на расстоянии 8см от центра пересекает плоскость. Радиус сечения равен-15см. Найдите площадь сферы.
2. Осевым сечением цилиндра является квадрат, диагональ которого равна 3 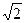 см. Найдите площадь поверхности цилиндра.
см. Найдите площадь поверхности цилиндра.
Вариант № 8.
1. Прямоугольный треугольник, гипотенуза которого равна 17см, а один из катетов-8см, вращается около этого катета. Найдите площадь поверхности тела вращения.
2. Высота прямой призмы равна 10см, а её основанием является прямоугольник, стороны которого равны 6см и 8см. Найдите площадь диагонального сечения.
Вариант № 9.
1. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания 10см и высота 12см, разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
2. Образующая конуса наклонена к плоскости основания под углом 300, а его высота равна 12см. Найдите площадь его боковой поверхности.
Вариант №10.
1. Два равных шара радиуса 5см расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности.


2. Площадь основания прямой треугольной призмы равна 4м2, а площади боковых граней 9, 10 и 17м2. Найдите объём призмы.
Вариант № 11.
1. Диагональ правильной четырёхугольной призмы равна 3,5см, а диагональ боковой грани 2,5см. Найдите объём призмы.
2. В прямой треугольной призме стороны оснований равны 4, 5 и 7см, а боковое ребро равно большей высоте основания. Найдите объём призмы.
Вариант № 12.
1. Диагональ квадрата, лежащего в основании правильной пирамиды, равна 8дм, а её высота 12дм. Найдите объём пирамиды.
2. Образующая конуса, равная 5см, составляет с плоскостью основания угол 450. Найдите объём конуса.
Вариант №13.
1. Шар с центром в точке О касается плоскости в точке А. Точка В лежит в плоскости касания. Найдите объём шара, если АВ=21 см, ВО=29 см.


2. В правильной треугольной призме АВСА1В1С1 проведено сечение через вершину С1 и ребро АВ. Найдите периметр сечения, если сторона основания равна 24см, а боковое ребро -10см.
Вариант №14.
1. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
2. В прямоугольном параллелепипеде стороны основания равны 5см и 12см, а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
Вариант № 15.
1. Образующая конуса равна 25см, а радиус основания-7см. Найдите его объём.
2. В правильной четырёхугольной пирамиде высота равна 12см, а апофема-15см. Найдите боковое ребро пирамиды.
Вариант № 16.
1. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
2. В правильной четырёхугольной пирамиде высота равна 7см, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды.
Вариант № 17.
1. Радиус основания цилиндра равен 5см, а его образующая-9см. Найдите площадь осевого сечения.
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота-12см. Найдите площадь полной поверхности пирамиды.
Вариант № 18.
1. Радиус основания конуса равен 14см. Найдите площадь сечения, проведённого перпендикулярно его оси через её середину.
2. В основании прямого параллелепипеда лежит ромб, диагонали которого равны 12см и 16см. Высота параллелепипеда-8см. Найдите площадь его полной поверхности.
Вариант № 19.
1. Сферу на расстоянии 8см от центра пересекает плоскость. Радиус сечения равен-15см. Найдите площадь сферы.
2. Осевым сечением цилиндра является квадрат, диагональ которого равна 3 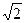 см. Найдите площадь поверхности цилиндра.
см. Найдите площадь поверхности цилиндра.
Вариант № 20.
1. Прямоугольный треугольник, гипотенуза которого равна 17см, а один из катетов-8см, вращается около этого катета. Найдите площадь поверхности тела вращения.
2. Высота прямой призмы равна 10см, а её основанием является прямоугольник, стороны которого равны 6см и 8см. Найдите площадь диагонального сечения.
Вариант № 21.
1. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания 10см и высота 12см, разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
2. Образующая конуса наклонена к плоскости основания под углом 300, а его высота равна 12см. Найдите площадь его боковой поверхности.
Вариант №22.
1. Два равных шара радиуса 5см расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности.


2. Площадь основания прямой треугольной призмы равна 4м2, а площади боковых граней 9, 10 и 17м2. Найдите объём призмы.
Вариант № 23.
1. Диагональ правильной четырёхугольной призмы равна 3,5см, а диагональ боковой грани 2,5см. Найдите объём призмы.
2. В прямой треугольной призме стороны оснований равны 4, 5 и 7см, а боковое ребро равно большей высоте основания. Найдите объём призмы.
Вариант № 24.
1. Диагональ квадрата, лежащего в основании правильной пирамиды, равна 8дм, а её высота 12дм. Найдите объём пирамиды.
2. Образующая конуса, равная 5см, составляет с плоскостью основания угол 450. Найдите объём конуса.
Вариант №25.
1. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
2. В прямоугольном параллелепипеде стороны основания равны 5см и 12см, а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
Вариант № 26.
1. Образующая конуса равна 25см, а радиус основания-7см. Найдите его объём.
2. В правильной четырёхугольной пирамиде высота равна 12см, а апофема-15см. Найдите боковое ребро пирамиды.
Вариант № 27.
1. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
2. В правильной четырёхугольной пирамиде высота равна 7см, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды.
Вариант № 28.
1. Радиус основания цилиндра равен 5см, а его образующая-9см. Найдите площадь осевого сечения.
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота-12см. Найдите площадь полной поверхности пирамиды.
Вариант № 29.
1. Прямоугольный треугольник, гипотенуза которого равна 17см, а один из катетов-8см, вращается около этого катета. Найдите площадь поверхности тела вращения.
2. Высота прямой призмы равна 10см, а её основанием является прямоугольник, стороны которого равны 6см и 8см. Найдите площадь диагонального сечения.
Вариант № 30.
1. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания 10см и высота 12см, разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
2. Образующая конуса наклонена к плоскости основания под углом 300, а его высота равна 12см. Найдите площадь его боковой поверхности.
Экзаменационные вопросы
1. Функции, их свойства и способы задания
2. Графики элементарных функций
3. Предел функции в точке
4. Предел функции на бесконечности
5. Степень с действительным показателем
6. Логарифмы и их свойства
7. Показательная функция, её свойства и график.
8. Логарифмическая функция, её свойства и график
9. Показательные уравнения
10. Показательные неравенства
11. Логарифмические уравнения
12. Логарифмические неравенства
13. Тригонометрические функции числового аргумента
14. Формулы приведения
15. Функции у = sin x, y = cos x, их свойства и графики
16. Функции y = tg x, y = ctg x, их свойства и графики
17. Обратные тригонометрические функции, их свойства и графики
18. Простейшие тригонометрические уравнения
19. Простейшие тригонометрические неравенства
20. Производная функции. Общее правило дифференцирования
21. Правила дифференцирования. Основные формулы дифференцирования
22. Производная сложной функции
23. Геометрический и физический смыслы производных
24. Монотонность и точки экстремума функции.
25. Наибольшее и наименьшее значения функции
26. Полное исследование функции с помощью производной и построение графика
27. Первообразная функции и её свойства.
28. Неопределённый интеграл и его свойства
29. Основные формулы интегрирования
30. Определённый интеграл и его свойства
31. Площадь криволинейной трапеции
32. Объём тел вращения
33. Векторы на плоскости. Основные характеристики. Действия над векторами
34. Векторы в пространстве. Основные характеристики. Действия над векторами
35. Скалярное произведение векторов. Угол между векторами
36. Аксиомы стереометрии и следствия из них
37. Взаимное расположения прямых в пространстве
38. Взаимное расположение прямой и плоскости в пространстве.
39. Перпендикулярность прямой и плоскости
40. Взаимное расположение плоскостей
41. Двугранные и многогранные углы
42. Перпендикулярность плоскостей.
43. Призма. Площадь поверхности призмы. Объём призмы
44. Параллелепипед и его свойства. Площадь поверхности параллелепипеда. Объём параллелепипеда
45. Пирамида. Площадь её поверхности. Объём пирамиды
46. Усечённая пирамида. Площадь её поверхности. Объём усечённой пирамиды
47. Конус. Площадь поверхности конуса. Объём конуса
48. Усечённый конус. Площадь поверхности. Объём усечённого конуса
49. Цилиндр. Площадь поверхности цилиндра. Объём цилиндра
50. Сфера. Уравнение сферы
51. Шар. Его части. Площадь поверхности
52. Объём шара и его частей
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы:
а) Основные источники, в т.ч. из ЭБС:
1. Баврин И. И. Математика. Учебник и практикум для СПО / И. И. Баврин. — 2-е изд. испр. и доп. - Москва : Издательство Юрайт, 2017. – 616 с
2. Мордкович А.Г., Семенов П.В.Математика: алгебра и начала математического анализа, геометрия. 10-11 классы. Алгебра и начала математического анализа. В 2 ч. Ч. 1. Учебник для учащихся образовательных организаций (базовый уровень) / А.Г. Мордкович. – 3-е изд., стер. – М.: Мнемозина, 2015. – 448 с.
3. Мордкович А.Г., Семенов П.В.Математика: алгебра и начала математического анализа, геометрия. 10-11 классы. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся образовательных организаций (базовый уровень) / А.Г. Мордкович. – 3-е изд., стер. – М.: Мнемозина, 2015. – 271 с.
4. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы. Учебник для общеобразовательных организаций (базовый и углубленный уровни) / Л.С. Атанасян. – М.: Просвещение, 2017. – 256 с.
б) Дополнительная литература, в т.ч. из ЭБС:
1. Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — Москва : Юрайт, 2016. — 285 с
2. Богомолов, Н. В. Математика. Задачи с решениями в 2 ч. Часть 2 : учебное пособие для СПО / Н. В. Богомолов. — 2-е изд., испр. и доп. — Москва : Юрайт, 2016. — 285 с
3. Лисичкин, В.Т. Математика в задачах с решениями. [Электронный ресурс] : Учебные пособия / В.Т. Лисичкин, И.Л. Соловейчик. — Электрон.дан. — СПб. : Лань, 2014. — Режим доступа: http://e.lanbook.com/book/2785 — Загл. с экрана.
в) Ресурсы сети «Интернет»:
1. https://e.lanbook.com/ - Электронно-библиотечная система издательства Лань.
2. http://www.iprbookshop.ru/ - Электронно-библиотечная система IPRbooks.
3. https://www.biblio-online.ru/ - Электронная библиотека ЮРАЙТ.
4. http://znanium.com/ - Электронно-библиотечная система Znanium.com.
Приложение 1
Дата: 2019-12-10, просмотров: 434.