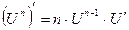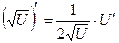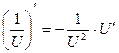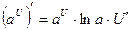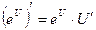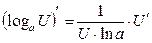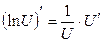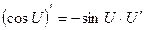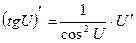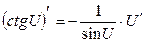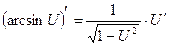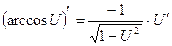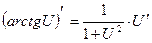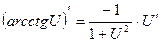МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по организации самостоятельной работы
И выполнению контрольной работы
по учебному предмету
ОУД.01 Математика: алгебра, начала анализа и геометрия
для обучающихся заочной формы обучения
специальности 23.02.03
Техническое обслуживание и ремонт автомобильного транспорта
Составитель: О.П. Проскурина
преподаватель Колледжа ПсковГУ
Псков
2018
Методические указания рассмотрены и рекомендованы к утверждению на заседании предметной цикловой комиссии ____________________________________________________________________________________________________________________________________
протокол №________ от «______» ____________ 20 г.
Председатель цикловой комиссии ________________ (Фамилия И.О.)
подпись
«________»_____________20 г.
СОДЕРЖАНИЕ
1. Пояснительная записка.
2. Методические указания к выполнению контрольной работы.
3. Варианты заданий для контрольной работы.
4. Экзаменационные вопросы.
5. Список рекомендуемой литературы.
6. Приложения.
Пояснительная записка
Рабочая программа учебного предмета “ Математика: алгебра, начала анализа и геометрия ” предназначена для реализации государственных требований к минимуму содержания и уровню подготовки выпускников заочного отделения по специальности СПО 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта» среднего профессионального образования.
Математика необходима для изучения программирования, математической статистики, математических методов и специальных дисциплин.
В методических указаниях приведены требования к основным знаниям и умениям, которые определяют обязательный минимальный уровень подготовки обучающихся по основному материалу.
Обучающиеся должны приобрести ряд общих знаний и навыков, необходимых для успешного усвоения математики, использования её при изучении специальных дисциплин, в курсовом и дипломном проектировании. Они должны уметь: делать ссылки на ранее изучаемый материал, самостоятельно изучать материал по учебной литературе, пользоваться справочными пособиями, предназначенными для средних специальных учебных заведений.
Обучающиеся должны усвоить, что математические понятия характеризуют свойства и отношения объектов реального мира, обладают широкой сферой применимости.
ПАСПОРТ ПРОГРАММЫ УЧЕБНОГО ПРЕДМЕТА
1.1. Цели и задачи предмета:
систематизация, обобщение математических знаний по математике, применение при решении задач; интеллектуальное развитие;
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики; развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования.
1.2. Место учебного предмета в структуре ППССЗ:
Учебный предмет «Математика: алгебра, начала анализа и геометрия» принадлежит к математическому и общему естественнонаучному циклу.
1.3. Требования к результатам освоения учебного предмета:
В результате освоения учебной дисциплины обучающийся должен:
Знать:
· Основные математические понятия;
· Основные правила и свойства, изучаемого понятия
· Основные правила при решении линейных уравнений. Формулы
решения квадратных уравнений
· Способы решения уравнений и неравенств;
· Понятие функции, её области определения области значений функции
· Понятие предела функции в точке и на бесконечности
· Понятие логарифма. Основные свойства логарифмов
· Способы решения логарифмических уравнений и неравенств
· Методы решения показательных уравнений и неравенств
· Основные формулы тригонометрии
· Определения и свойства обратных тригонометрических функций.
· Формулы решения тригонометрических уравнений
· Понятие производной. Правила и основные формулы вычисления
производных
· Геометрический смысл 1-ой и 2-ой производной
· Понятие возрастания и убывания функций; признаки монотонности
· Понятие наибольшего и наименьшего значения функции на отрезке. Алгоритм нахождения наибольшего и наименьшего значения функции на промежутке
· Понятие неопределённого интеграла и его свойства. Основные формулы интегрирования
· Понятие определённого интеграла и его свойства
· Формулы площади геометрических фигур
· Формулы объёмов тел
Уметь:
· Делать ссылки на ранее изученный материал;
· Самостоятельно изучать материал по учебной литературе;
· Пользоваться справочными пособиями, предназначенными для обучающихся средних специальных образовательных учреждений.
· Решать линейные, квадратные уравнения и неравенства
· Решать системы уравнений и неравенств с одной переменной
· Находить область определения функции, определять четность функции
· Вычислять предел функции в точке и на бесконечности
· Вычислять логарифмы
· Решать логарифмические уравнения и неравенства
· Решать показательные уравнения и неравенства
· Строить графики тригонометрических функций y 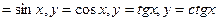
· Преобразовывать тригонометрические выражения
· Решать тригонометрические уравнения и неравенства
· Находить производную функций
· Находить промежутки монотонности, промежутки знакопостоянства
· Находить наибольшее и наименьшее значение функции на отрезке
· Находить неопределённый интеграл
· Вычислять определённый интеграл. Вычислять площадь фигур
· Вычислять площади геометрических тел
· Вычислять объём тел
В процессе изучения предмета «Математика: алгебра, начала анализа и геометрия» выполняется домашняя контрольная работа и итоговая аттестация в виде экзамена.
При проверке домашней контрольной работы «зачёт» ставится при условии, что работа выполнена полностью и без ошибок, либо при наличии не значительных недочётов. В противном случае работа возвращается на доработку.
Итоговая аттестация – экзамен проводится по билетам, содержащим два теоретических и два практических вопроса (критерии оценки изложены в приложении 2).
Время на проведение перечисленных мероприятий выделяется из общего числа учебных часов.
Тематический план и содержание учебного предмета
Для заочной формы обучения
| Наименование разделов и тем | Содержание учебного материала, практические занятия, самостоятельные работы, проверочные работы обучающихся | Объём часов | Уровень освоения |
| Раздел 1 | Повторение | 22 | |
| Формулы сокращенного умножения | Содержание учебного материала: Формулы сокращенного умножения. Свойства степени. Упрощение выражений. | - | 1,2 |
| Уравнения. Системы уравнений | Содержание учебного материала: Линейные уравнения. Квадратные уравнения. Биквадратные уравнения. Рациональные уравнения. Иррациональные уравнения. Систем уравнений. | ||
| Неравенства. Системы неравенств. | Содержание учебного материала: Неравенства и их виды. Системы неравенств. | ||
| Практическое занятие | 2 | 3 | |
| Самостоятельная работа обучающихся | 20 | 3 | |
| Раздел 2 | Функции, их свойства и графики | 34 | |
| Функции, их свойства и графики | Содержание учебного материала: Функции и их свойства. Функции, способы её задания. Графики элементарных функций. | 2 | 1,2 |
| Предел функции | Содержание учебного материала: Предел функции в точке. Предел функции на бесконечности. | ||
| Практическое занятие | 2 | 3 | |
| Самостоятельная работа обучающихся | 30 | 3 | |
| Раздел 3 | Показательная и логарифмическая функция | 54 | |
| Логарифмы и их свойства | Содержание учебного материала: Степень с действительным показателем. Понятие логарифма. Свойства логарифмов. | 2 | 1,2 |
| Показатель-ная функция | Содержание учебного материала: Показательная функция. Свойства показательной функции. График показательной функции. | ||
| Логарифми-ческая функция | Содержание учебного материала: Логарифмическая функция. Свойства логарифмической функции. График логарифмической функции. | ||
| Показатель-ные уравнения и неравенства | Содержание учебного материала: Показательные уравнения Показательные неравенства | ||
| Логарифми-ческие уравнения и неравенства | Содержание учебного материала: Логарифмические уравнения Логарифмические неравенства | ||
| Практическое занятие | 2 | 3 | |
| Самостоятельная работа обучающихся | 50 | 3 | |
| Раздел 4 | Тригонометрические функции | 44 | |
| Тригонометрические функции числового аргумента | Содержание учебного материала: Тригонометрические функции числового аргумента Функция у = sin x и её свойства Функция y = cos x и её свойства Функция y = tg x и её свойства Функция y = ctg x и её свойства Построение графиков тригонометрических функций | 2 | 1,2 |
| Формулы тригономет-рии | Содержание учебного материала: Формулы приведения Формулы сложения тригонометрических функций Формулы суммы и разности углов Формулы двойного угла. Преобразование тригонометрических выражений | ||
| Тригонометрические уравнения и неравенства | Содержание учебного материала: Обратные тригонометрические функции Графики обратных тригонометрических функций Тригонометрические уравнения Тригонометрические неравенства | ||
| Практическое занятие | 2 | 3 | |
| Самостоятельная работа обучающихся | 40 | 3 | |
| Раздел 5. | Производная функции и её приложение | 56 | |
| Производная функции. Общее правило дифферен-цирования | Содержание учебного материала: Определение производной функции Общее правило дифференцирования. | 3 | 1,2 |
| Дифферен-цирование функций | Содержание учебного материала: Производная степенной функции Правила дифференцирования. Производная тригонометрических функций Производная обратных тригонометрических функций Производная показательной и логарифмической функции Производная сложной функции | ||
| Геометричес-кий и физический смыслы производных | Содержание учебного материала: Геометрический смысл производной Физический смысл производной | ||
| Исследование функции и построение её графика с помощью производной | Содержание учебного материала: Монотонность функции Точки экстремума функции Наибольшее и наименьшее значения функции Полное исследование функции и построение её графика | ||
| Практическое занятие | 3 | 3 | |
| Самостоятельная работа обучающихся | 50 | 3 | |
| Раздел 6. | Интеграл и его приложение. | 44 | |
| Неопределён-ный интеграл | Содержание учебного материала: Первообразная функции и её свойства Неопределённый интеграл и его свойства Основные формулы интегрирования Непосредственное интегрирование | 2 | 1,2 |
| Определён-ный интеграл | Содержание учебного материала: Определённый интеграл и его свойства Геометрический смысл определённого интеграла Вычисление площади криволинейной трапеции Объёмы тел вращения | ||
| Практическое занятие | 2 | 3 | |
| Самостоятельная работа обучающихся | 40 | 3 | |
| Раздел 7. | Векторы в пространстве | 22 | |
| Векторы на плоскости | Содержание учебного материала: Векторы на плоскости Основные характеристики Действия над векторами на плоскости | 1 | 1,2 |
| Векторы в пространстве | Содержание учебного материала: Векторы в пространстве Основные характеристики Действия над векторами в пространстве | ||
| Скалярное произведение векторов | Содержание учебного материала: Скалярное произведение векторов Угол между векторами | ||
| Практическое занятие | 1 | 3 | |
| Самостоятельная работа обучающихся | 20 | 3 | |
| Раздел 8. | Прямые и плоскости в пространстве | 32 | |
| Прямые и плоскости в пространстве | Содержание учебного материала: Аксиомы стереометрии и следствия из них Взаимное расположение прямой и плоскости в пространстве Взаимное расположения прямых в пространстве Перпендикулярность прямой и плоскости Взаимное расположение плоскостей Двугранные и многогранные углы Перпендикулярность плоскостей | 2 | 1,2 |
| Практическое занятие | - | 3 | |
| Самостоятельная работа обучающихся | 30 | 3 | |
| Раздел 9. | Геометрические тела и их поверхности | ||
| Многогран-ники | Содержание учебного материала: Призма Площадь поверхности призмы Параллелепипед и его свойства Объём призмы Пирамида. Площадь поверхности пирамиды Усечённая пирамида Площадь поверхности усечённой пирамиды Объём пирамиды и усечённой пирамиды | 2 | 1,2 |
| Тела вращения | Содержание учебного материала: Конус Площадь поверхности конуса Усечённый конус и его поверхность Объём конуса и усечённого конуса Цилиндр. Площадь поверхности цилиндра Объём цилиндра Сфера. Уравнение сферы Шар и его части Площадь поверхности шара и его частей Объём шара и его частей | ||
| Практическое занятие | 2 | 3 | |
| Самостоятельная работа обучающихся | 39 | 3 | |
| Итого | 351 |
Для характеристики уровня освоения учебного материала используются следующие обозначения:
1. – ознакомительный (узнавание ранее изученных объектов, свойств);
2. – репродуктивный (выполнение деятельности по образцу, инструкции или под руководством)
3. – продуктивный (планирование и самостоятельное выполнение деятельности, решение проблемных задач)
Методические рекомендации для выполнения самостоятельных и контрольных работ
Приступая к изучению предмета необходимо ознакомиться с содержанием программы и составить план занятий, т. е. разделить материал на последовательно изучаемые темы. После этого в каждой теме следует выделить основные вопросы, чтобы затем, в процессе изучения материала, найти на них ответы.
Одним из важнейших средств активизации самостоятельной творческой деятельности студентов является умение решать задачи. Для этого необходимо внимательно изучить условие задачи, проанализировать содержание, выяснить закономерности и правила, лежащие в основе её решения.
Конечно, общих рецептов для решения разнообразных задач не существует, однако рекомендуем придерживаться следующих советов:
1. Внимательно изучите цель, поставленную в задаче; выясните, какие теоретические положения связаны с данной задачей в целом или с некоторыми её элементами.
2. Не следует приступать к решению задачи, не обдумав её условия и не найдя плана решения.
3. Попробуйте расчленить данную задачу на серию вспомогательных, последовательное решение которых может составить решение исходной задачи.
4. Найдя план решения, выполните его, убедитесь в необходимости и правильности каждого шага, произведите проверку решения.
5. Подумайте, нельзя ли было решить задачу иначе; известно, что каждая задача может иметь несколько решений, поэтому следует выделить наиболее рациональное.
6. Если решить задачу не удаётся, отыщите в учебной литературе уже решённую задачу, похожую на данную, изучите внимательно это решение и постарайтесь извлечь из него пользу для решения данной задачи.
Необходимо приучить себя к постоянному самоконтролю в процессе своей работы. При решении задачи следует приучиться проверять каждый свой шаг, оценивать его разумность, рациональность, необходимость и полезность.
При этом могут использоваться различные приемы самоконтроля: проверка результатов решения задачи, проверка по аналогичному заданию, проверка с помощью обратных действий, оценка соответствия результата здравому смыслу.
Решив задачу, проанализируйте решение, отметьте, что нового при этом вы узнали и приобрели. Постарайтесь запомнить и усвоить те приёмы, которые вы использовали. Все это пригодится при решении других задач.
Контрольная работа содержит задания из разных тем. При решении заданий на тему:
- «Уравнения и неравенства» следует применять формулы упрощения многочленов, свойства уравнений и неравенств;
- «Пределы функции в точке и на бесконечности» следует применять определения пределов в точке и на бесконечности, их свойства, понятия бесконечно большой и бесконечно малой величин, уметь раскрывать неопределенности 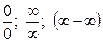 .
.
- «Показательная и логарифмическая функции» следует применять свойства степеней, свойства логарифмов, свойства показательной и логарифмической функций:
Свойства степеней:
1). а0 = 1
2). а1 = а
3). (аm)n = аmn
4). аm·an = аm+n
5). 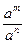 = аm-n
= аm-n
6). (abc)m = am bmcm
7). 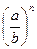 =
= 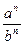
8). 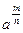 =
= 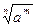
9). 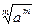 = a
= a
10). 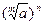 =
= 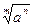
11). 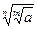 =
= 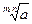
12). 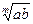 =
= 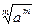
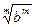
13). 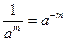
Логарифмом положительного числа b по основанию a, называется показатель степени с, в которую нужно возвести основание а, чтобы получить число b, причём b>0, а>0 и а≠1.
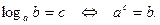
|
Основное логарифмическое тождество:
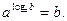
|
Основные свойства логарифмов:
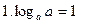 (а>0, а≠1);
(а>0, а≠1);
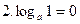 (а>0, а≠1);
(а>0, а≠1);
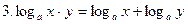 (а>0, а≠1, x>0, y>0);
(а>0, а≠1, x>0, y>0);
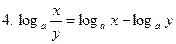 (а>0, а≠1, x>0, y>0);
(а>0, а≠1, x>0, y>0);
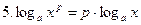 (а>0, а≠1, x>0);
(а>0, а≠1, x>0);
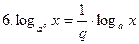 (а>0, а≠1, x>0, q≠0);
(а>0, а≠1, x>0, q≠0);
7. Переход к новому основанию:
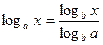 (а>0, а≠1, x>0, b>0, b≠1);
(а>0, а≠1, x>0, b>0, b≠1);
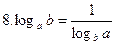 (а>0, а≠1, b>0, b≠1).
(а>0, а≠1, b>0, b≠1).
- «Тригонометрия» следует применять формулы тригонометрии, свойства уравнений и неравенств;
- «Производная функции» следует применять определение производной функции, правила дифференцирования функции, и основные формулы дифференцирования.
Правила дифференцирования:
Пусть U и V – функции переменной x ,
С – постоянная величина.
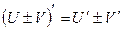
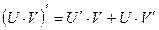
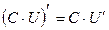
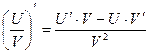
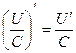
| Формулы дифференцирования: | ||
| Элементарны функции: | Сложные функции: | |
1. 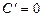
| - | |
2. 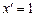
| - | |
3. 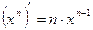
|
| |
4. 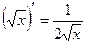
|
| |
5. 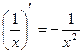
|
| |
6. 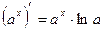
|
| |
7. 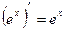
|
| |
8. 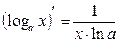
|
| |
9. 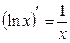
|
| |
10. 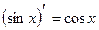
|
| |
11. 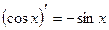
|
| |
12. 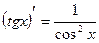
|
| |
13. 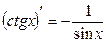
|
| |
14. 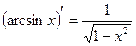
|
| |
15. 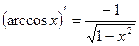
|
| |
16. 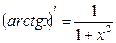
|
| |
17. 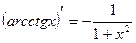
|
| |
- «Неопределённый интеграл» следует применять свойства неопределенного интеграла, основные формулы интегрирования и если после алгебраических преобразований нельзя применить формулы интегрирования, то необходимо воспользоваться методом подстановки, методом интегрирования по частям или методом интегрирования рациональных дробей.
Контрольная работа
Требования к оформлению контрольной работы
Контрольную работу следует выполнять в ученических тетрадях (желательно в клеточку). На обложке необходимо указать: название учебного заведения, название специальности, курс, номер группы, фамилию, имя, отчество и личный номер студента (который определяется по номеру в журнале группы). Условия задач переписывать не обязательно, достаточно указать номер задачи.
Повторение
Уравнения
Решить уравнения:
Вариант №1.
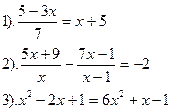
| Вариант №2.
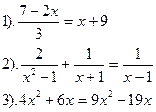
| Вариант №3.
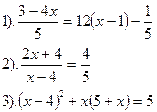
|
Вариант №4.
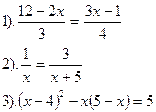
| Вариант №5.
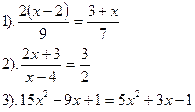
| Вариант №6.
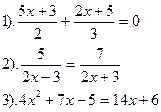
|
Вариант №7.
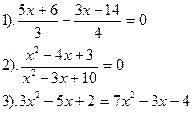
| Вариант №8.
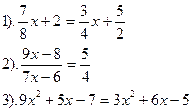
| Вариант №9.
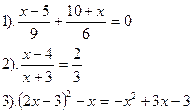
|
Вариант №10.
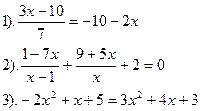
| Вариант №11.
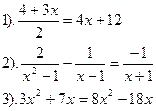
| Вариант №12.
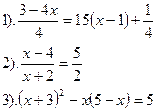
|
Вариант №13.
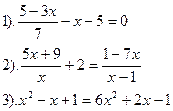
| Вариант №14.
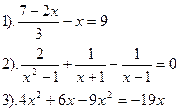
| Вариант №15.
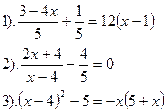
|
Вариант №16.
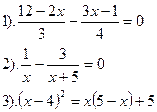
| Вариант №17.
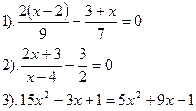
| Вариант №18.
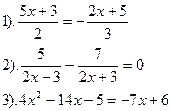
|
Вариант №19.
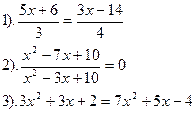
| Вариант №20.
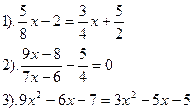
| Вариант №21.
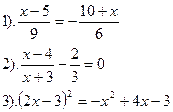
|
Вариант №22.
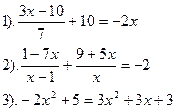
| Вариант №23.
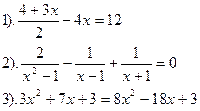
| Вариант №24.
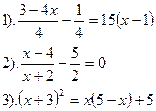
|
Вариант №25.
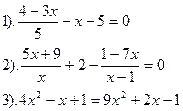
| Вариант №26.
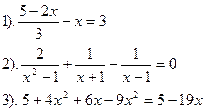
| Вариант №27.
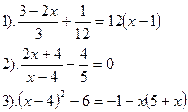
|
Вариант №28.
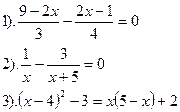
| Вариант №29.
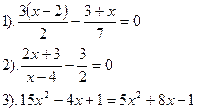
| Вариант №30.
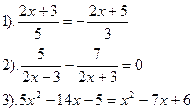
|
Неравенства
Решить неравенства:
Вариант №1.
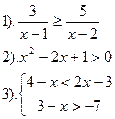
| Вариант №2.
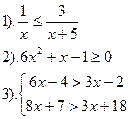
| Вариант №3.
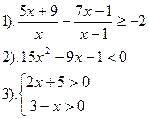
|
Вариант №4.
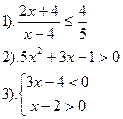
| Вариант №5.
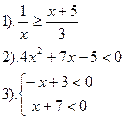
| Вариант №6.
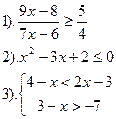
|
Вариант №7.
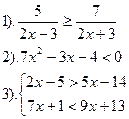
| Вариант №8.
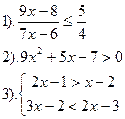
| Вариант №9.
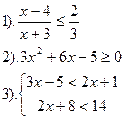
|
Вариант №10.

| Вариант №11.
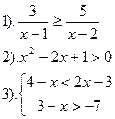
| Вариант №12.
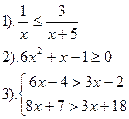
|
Вариант №13.
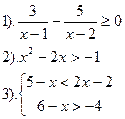
| Вариант №14.
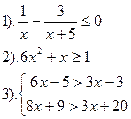
| Вариант №15.
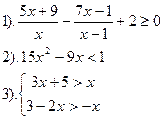
|
Вариант №16.
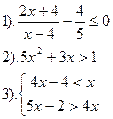
| Вариант №17.
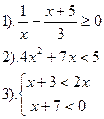
| Вариант №18.
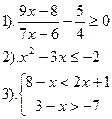
|
Вариант №19.
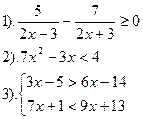
| Вариант №20.
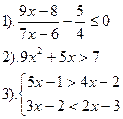
| Вариант №21.
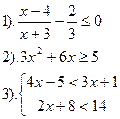
|
Вариант №22.
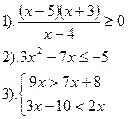
| Вариант №23.
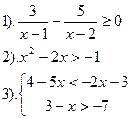
| Вариант №24.
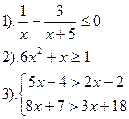
|
Вариант №25.
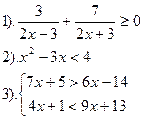
| Вариант №26.
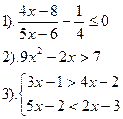
| Вариант №27.

|
Вариант №28.
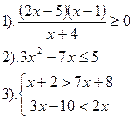
| Вариант №29.
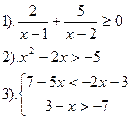
| Вариант №30.
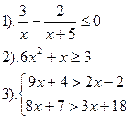
|
Теория пределов
Пределы
Вычислить:
Вариант №1.

| Вариант №2.
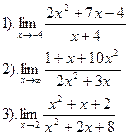
| Вариант №3.
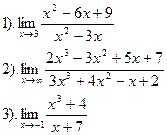
|
Вариант №4.
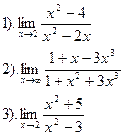
| Вариант №5.
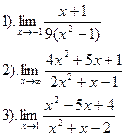
| Вариант №6.
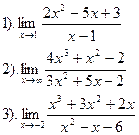
|
Вариант №7.
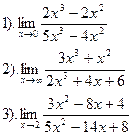
| Вариант №8.
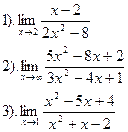
| Вариант №9.
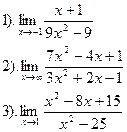
|
Вариант №10.
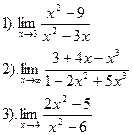
| Вариант №11.
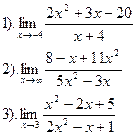
| Вариант №12.
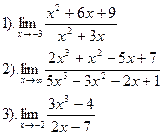
|
Вариант №13.
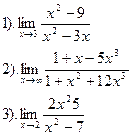
| Вариант №14.
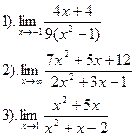
| Вариант №15.
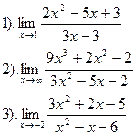
|
Вариант №16.
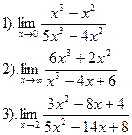
| Вариант №17.
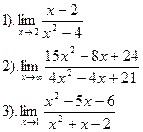
| Вариант №18.
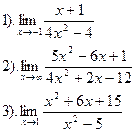
|
Вариант №19.
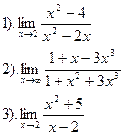
| Вариант №20.
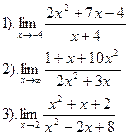
| Вариант №21.
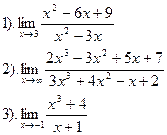
|
Вариант №22.
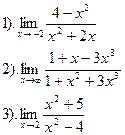
| Вариант №23.
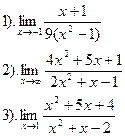
| Вариант №24.
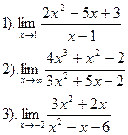
|
Вариант №25.
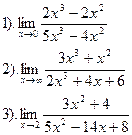
| Вариант №26.

| Вариант №27.
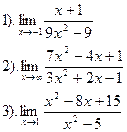
|
Вариант №28.
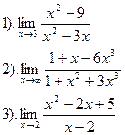
| Вариант №29.
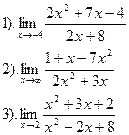
| Вариант №30.
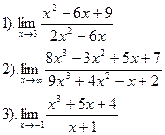
|
Показательная функция
Вариант №1.
Сравнить:
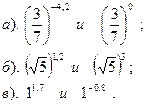
| Вариант №2.
Сравнить:
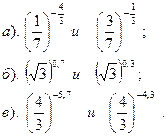
| Вариант №3.
Сравнить:
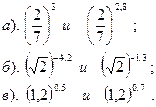
| Вариант №4.
Сравнить:
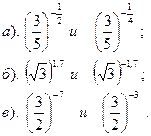
|
Вариант №5.
Сравнить:
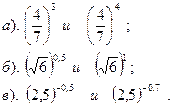
| Вариант №6.
Сравнить:
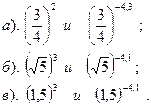
| Вариант №7.
Сравнить:
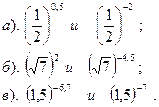
| Вариант №8.
Сравнить: 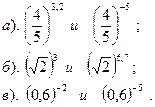
|
Вариант №9.
Сравнить показатели степени:
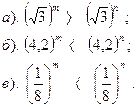
| Вариант №10.
Сравнить показатели степени:
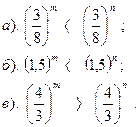
| Вариант №11.
Сравнить показатели степени:
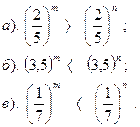
| Вариант №12.
Сравнить показатели степени:
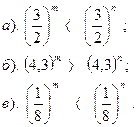
|
Вариант №13.
Сравнить:
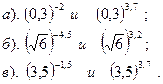
| Вариант №14. Сравнить показатели степени:
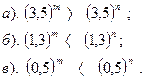
| Вариант №15. . Сделать вывод об основании степени:
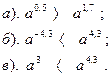
| Вариант №16. Сравнить показатели степени:

|
Вариант №17. Сравнить:
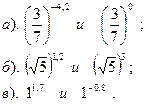
| Вариант №18. Сравнить:
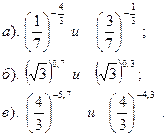
| Вариант №19. Сравнить:
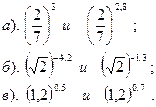
| Вариант №20. Сравнить:
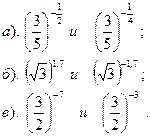
|
Вариант №21. Сравнить:
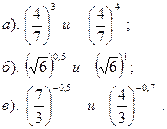
| Вариант №22. Сравнить показатели степени:
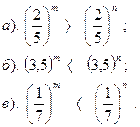
| Вариант №23. Сравнить показатели степени:
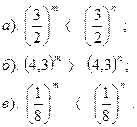
| Вариант №24. Сравнить показатели степени:
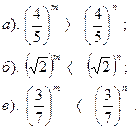
|
Вариант №25. Сравнить показатели степени:
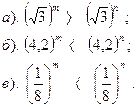
| Вариант №26. Сравнить показатели степени:
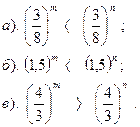
| Вариант №27. Сравнить:
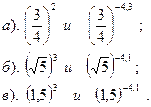
| Вариант №28. Сравнить:
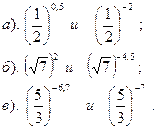
|
Вариант №29. Сравнить:
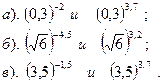
| Вариант №30. Сравнить показатели степени:
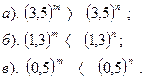
|
Приложение производной
3.1 Найти производные функций:
Вариант №1.
Найти производные функций :
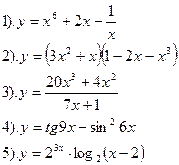
| Вариант №2.
Найти производные функций :
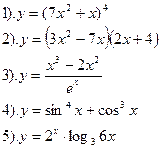
| Вариант №3.
Найти производные функций :
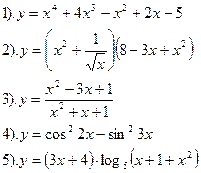
|
Вариант №4.
Найти производные функций :
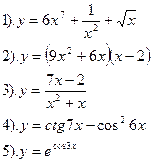
| Вариант №5.
Найти производные функций :
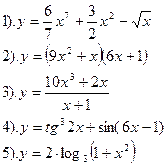
| Вариант №6.
Найти производные функций :
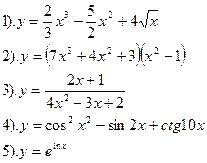
|
Вариант №7.
Найти производные функций :
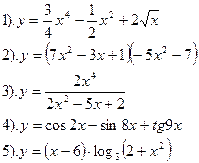
| Вариант №8.
Найти производные функций :
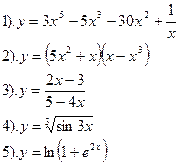
| Вариант №9.
Найти производные функций :
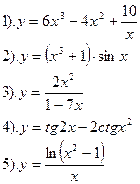
|
Вариант №10.
Найти производные функций :
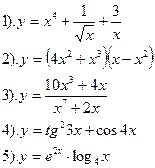
| Вариант №11.
Найти производные функций :
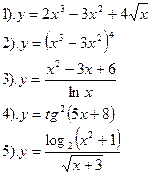
| Вариант №12.
Найти производные функций :
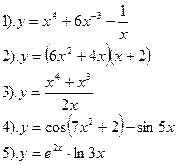
|
Вариант №13.
Найти производные функций:
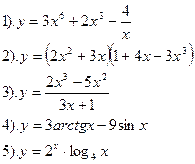
| Вариант №14.
Найти производные функций:
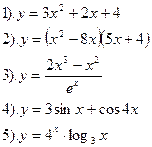
| Вариант №15.
Найти производные функций:
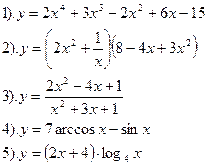
|
Вариант №16.
Найти производные функций:
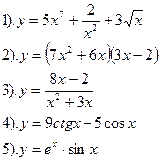
| Вариант №17.
Найти производные функций:

| Вариант №18.
Найти производные функций:
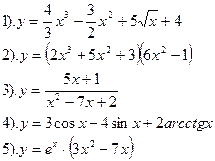
|
Вариант №19.
Найти производные функций:
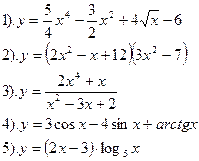
| Вариант №20.
Найти производные функций:
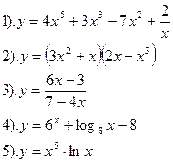
| Вариант №21.
Найти производные функций:
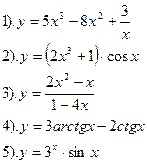
|
Вариант №22.
Найти производные функций:
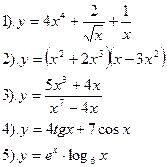
| Вариант №23.
Найти производные функций:
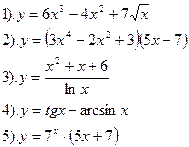
| Вариант №24.
Найти производные функций:
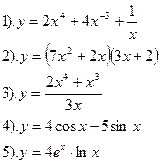
|
Вариант №25.
Найти производные функций:
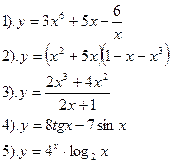
| Вариант №26.
Найти производные функций:
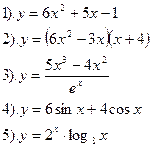
| Вариант №27.
Найти производные функций:
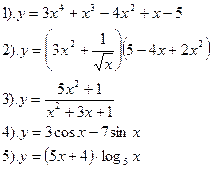
|
Вариант №28.
Найти производные функций:
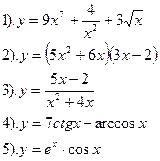
| Вариант №29.
Найти производные функций:
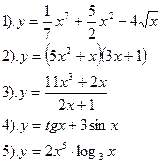
| Вариант №30.
Найти производные функций:
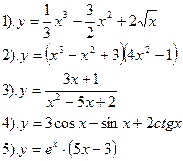
|
Неопределённый интеграл
Вариант №1.
Найти:
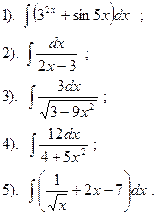
| Вариант №2.
Найти:
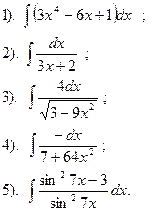
| Вариант №3.
Найти:
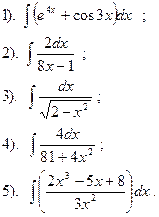
| Вариант №4.
Найти:
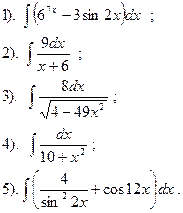
|
Вариант №5.
Найти:
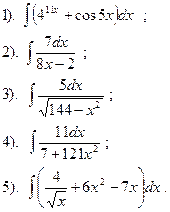
| Вариант №6.
Найти:
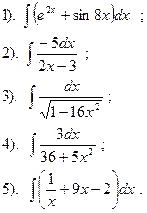
| Вариант №7.
Найти:
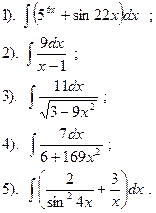
| Вариант №8.
Найти:
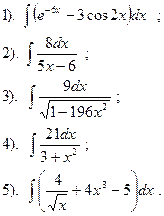
|
Вариант №9.
Найти:
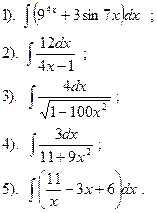
| Вариант №10.
Найти:
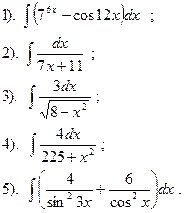
| Вариант №11.
Найти:
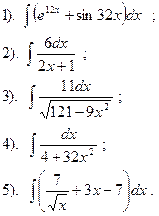
| Вариант №12.
Найти:
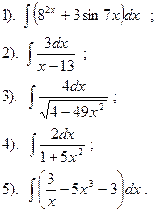
|
Вариант №13.
Найти:
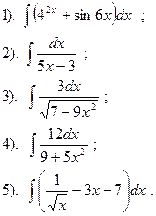
|
Вариант №14.
Найти:
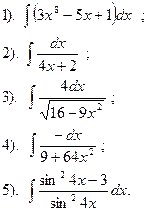
|
Вариант №15.
Найти:
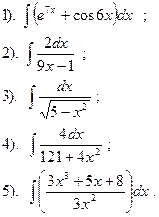
|
Вариант №16.
Найти:
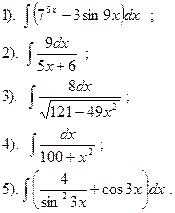
|
Вариант №17.
Найти:
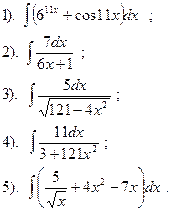
|
Вариант №18.
Найти:
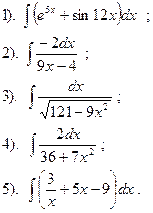
|
Вариант №19.
Найти:
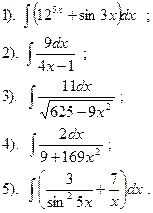
|
Вариант №20.
Найти:
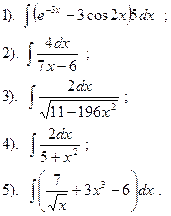
|
Вариант №21.
Найти:
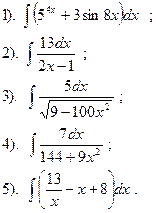
|
Вариант №22.
Найти:
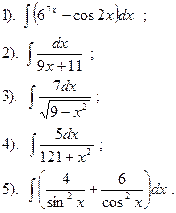
|
Вариант №23.
Найти:
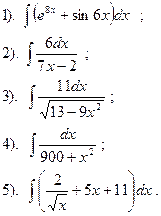
|
Вариант №24.
Найти:
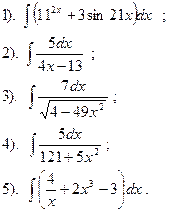
|
Вариант №25.
Найти:
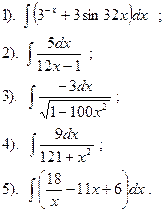
|
Вариант №26.
Найти:
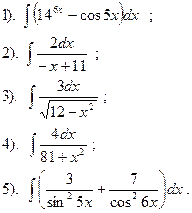
|
Вариант №27.
Найти:
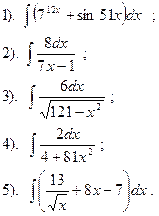
|
Вариант №28.
Найти:
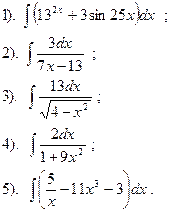
|
Вариант №29.
Найти:
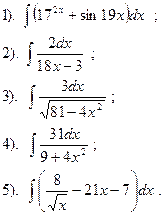
| Вариант №30.
Найти:
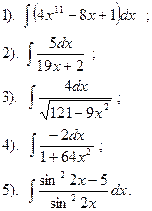
|
Определённый интеграл
Построить схематически чертёж и найти площадь фигуры, ограниченной линиями:
1. 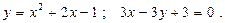
2. 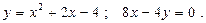
3. 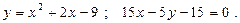
4. 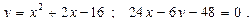
5. 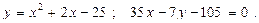
6. 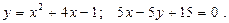
7. 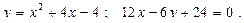
8. 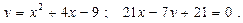
9. 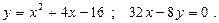
10. 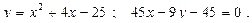
11. 
12. 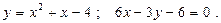
13. 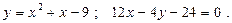
14. 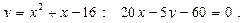
15. 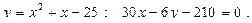
16. 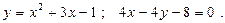
17. 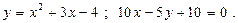
18. 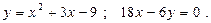
19. 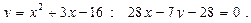
20. 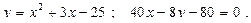
21. 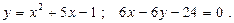
22. 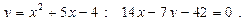
23. 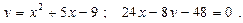
24. 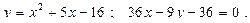
25. 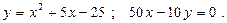
26. 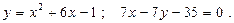
27. 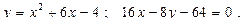
28. 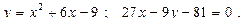
29. 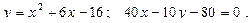
30. 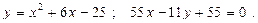
Геометрия
Вариант №1.
1. Шар с центром в точке О касается плоскости в точке А. Точка В лежит в плоскости касания. Найдите объём шара, если АВ=21 см, ВО=29 см.


2. В правильной треугольной призме АВСА1В1С1 проведено сечение через вершину С1 и ребро АВ. Найдите периметр сечения, если сторона основания равна 24см, а боковое ребро -10см.
Вариант №2.
1. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
2. В прямоугольном параллелепипеде стороны основания равны 5см и 12см, а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
Вариант № 3.
1. Образующая конуса равна 25см, а радиус основания-7см. Найдите его объём.
2. В правильной четырёхугольной пирамиде высота равна 12см, а апофема-15см. Найдите боковое ребро пирамиды.
Вариант № 4.
1. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
2. В правильной четырёхугольной пирамиде высота равна 7см, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды.
Вариант № 5.
1. Радиус основания цилиндра равен 5см, а его образующая-9см. Найдите площадь осевого сечения.
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота-12см. Найдите площадь полной поверхности пирамиды.
Вариант № 6.
1. Радиус основания конуса равен 14см. Найдите площадь сечения, проведённого перпендикулярно его оси через её середину.
2. В основании прямого параллелепипеда лежит ромб, диагонали которого равны 12см и 16см. Высота параллелепипеда-8см. Найдите площадь его полной поверхности.
Вариант № 7.
1. Сферу на расстоянии 8см от центра пересекает плоскость. Радиус сечения равен-15см. Найдите площадь сферы.
2. Осевым сечением цилиндра является квадрат, диагональ которого равна 3 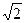 см. Найдите площадь поверхности цилиндра.
см. Найдите площадь поверхности цилиндра.
Вариант № 8.
1. Прямоугольный треугольник, гипотенуза которого равна 17см, а один из катетов-8см, вращается около этого катета. Найдите площадь поверхности тела вращения.
2. Высота прямой призмы равна 10см, а её основанием является прямоугольник, стороны которого равны 6см и 8см. Найдите площадь диагонального сечения.
Вариант № 9.
1. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания 10см и высота 12см, разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
2. Образующая конуса наклонена к плоскости основания под углом 300, а его высота равна 12см. Найдите площадь его боковой поверхности.
Вариант №10.
1. Два равных шара радиуса 5см расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности.


2. Площадь основания прямой треугольной призмы равна 4м2, а площади боковых граней 9, 10 и 17м2. Найдите объём призмы.
Вариант № 11.
1. Диагональ правильной четырёхугольной призмы равна 3,5см, а диагональ боковой грани 2,5см. Найдите объём призмы.
2. В прямой треугольной призме стороны оснований равны 4, 5 и 7см, а боковое ребро равно большей высоте основания. Найдите объём призмы.
Вариант № 12.
1. Диагональ квадрата, лежащего в основании правильной пирамиды, равна 8дм, а её высота 12дм. Найдите объём пирамиды.
2. Образующая конуса, равная 5см, составляет с плоскостью основания угол 450. Найдите объём конуса.
Вариант №13.
1. Шар с центром в точке О касается плоскости в точке А. Точка В лежит в плоскости касания. Найдите объём шара, если АВ=21 см, ВО=29 см.


2. В правильной треугольной призме АВСА1В1С1 проведено сечение через вершину С1 и ребро АВ. Найдите периметр сечения, если сторона основания равна 24см, а боковое ребро -10см.
Вариант №14.
1. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
2. В прямоугольном параллелепипеде стороны основания равны 5см и 12см, а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
Вариант № 15.
1. Образующая конуса равна 25см, а радиус основания-7см. Найдите его объём.
2. В правильной четырёхугольной пирамиде высота равна 12см, а апофема-15см. Найдите боковое ребро пирамиды.
Вариант № 16.
1. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
2. В правильной четырёхугольной пирамиде высота равна 7см, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды.
Вариант № 17.
1. Радиус основания цилиндра равен 5см, а его образующая-9см. Найдите площадь осевого сечения.
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота-12см. Найдите площадь полной поверхности пирамиды.
Вариант № 18.
1. Радиус основания конуса равен 14см. Найдите площадь сечения, проведённого перпендикулярно его оси через её середину.
2. В основании прямого параллелепипеда лежит ромб, диагонали которого равны 12см и 16см. Высота параллелепипеда-8см. Найдите площадь его полной поверхности.
Вариант № 19.
1. Сферу на расстоянии 8см от центра пересекает плоскость. Радиус сечения равен-15см. Найдите площадь сферы.
2. Осевым сечением цилиндра является квадрат, диагональ которого равна 3 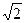 см. Найдите площадь поверхности цилиндра.
см. Найдите площадь поверхности цилиндра.
Вариант № 20.
1. Прямоугольный треугольник, гипотенуза которого равна 17см, а один из катетов-8см, вращается около этого катета. Найдите площадь поверхности тела вращения.
2. Высота прямой призмы равна 10см, а её основанием является прямоугольник, стороны которого равны 6см и 8см. Найдите площадь диагонального сечения.
Вариант № 21.
1. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания 10см и высота 12см, разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
2. Образующая конуса наклонена к плоскости основания под углом 300, а его высота равна 12см. Найдите площадь его боковой поверхности.
Вариант №22.
1. Два равных шара радиуса 5см расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности.


2. Площадь основания прямой треугольной призмы равна 4м2, а площади боковых граней 9, 10 и 17м2. Найдите объём призмы.
Вариант № 23.
1. Диагональ правильной четырёхугольной призмы равна 3,5см, а диагональ боковой грани 2,5см. Найдите объём призмы.
2. В прямой треугольной призме стороны оснований равны 4, 5 и 7см, а боковое ребро равно большей высоте основания. Найдите объём призмы.
Вариант № 24.
1. Диагональ квадрата, лежащего в основании правильной пирамиды, равна 8дм, а её высота 12дм. Найдите объём пирамиды.
2. Образующая конуса, равная 5см, составляет с плоскостью основания угол 450. Найдите объём конуса.
Вариант №25.
1. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
2. В прямоугольном параллелепипеде стороны основания равны 5см и 12см, а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
Вариант № 26.
1. Образующая конуса равна 25см, а радиус основания-7см. Найдите его объём.
2. В правильной четырёхугольной пирамиде высота равна 12см, а апофема-15см. Найдите боковое ребро пирамиды.
Вариант № 27.
1. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
2. В правильной четырёхугольной пирамиде высота равна 7см, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды.
Вариант № 28.
1. Радиус основания цилиндра равен 5см, а его образующая-9см. Найдите площадь осевого сечения.
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота-12см. Найдите площадь полной поверхности пирамиды.
Вариант № 29.
1. Прямоугольный треугольник, гипотенуза которого равна 17см, а один из катетов-8см, вращается около этого катета. Найдите площадь поверхности тела вращения.
2. Высота прямой призмы равна 10см, а её основанием является прямоугольник, стороны которого равны 6см и 8см. Найдите площадь диагонального сечения.
Вариант № 30.
1. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания 10см и высота 12см, разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
2. Образующая конуса наклонена к плоскости основания под углом 300, а его высота равна 12см. Найдите площадь его боковой поверхности.
Экзаменационные вопросы
1. Функции, их свойства и способы задания
2. Графики элементарных функций
3. Предел функции в точке
4. Предел функции на бесконечности
5. Степень с действительным показателем
6. Логарифмы и их свойства
7. Показательная функция, её свойства и график.
8. Логарифмическая функция, её свойства и график
9. Показательные уравнения
10. Показательные неравенства
11. Логарифмические уравнения
12. Логарифмические неравенства
13. Тригонометрические функции числового аргумента
14. Формулы приведения
15. Функции у = sin x, y = cos x, их свойства и графики
16. Функции y = tg x, y = ctg x, их свойства и графики
17. Обратные тригонометрические функции, их свойства и графики
18. Простейшие тригонометрические уравнения
19. Простейшие тригонометрические неравенства
20. Производная функции. Общее правило дифференцирования
21. Правила дифференцирования. Основные формулы дифференцирования
22. Производная сложной функции
23. Геометрический и физический смыслы производных
24. Монотонность и точки экстремума функции.
25. Наибольшее и наименьшее значения функции
26. Полное исследование функции с помощью производной и построение графика
27. Первообразная функции и её свойства.
28. Неопределённый интеграл и его свойства
29. Основные формулы интегрирования
30. Определённый интеграл и его свойства
31. Площадь криволинейной трапеции
32. Объём тел вращения
33. Векторы на плоскости. Основные характеристики. Действия над векторами
34. Векторы в пространстве. Основные характеристики. Действия над векторами
35. Скалярное произведение векторов. Угол между векторами
36. Аксиомы стереометрии и следствия из них
37. Взаимное расположения прямых в пространстве
38. Взаимное расположение прямой и плоскости в пространстве.
39. Перпендикулярность прямой и плоскости
40. Взаимное расположение плоскостей
41. Двугранные и многогранные углы
42. Перпендикулярность плоскостей.
43. Призма. Площадь поверхности призмы. Объём призмы
44. Параллелепипед и его свойства. Площадь поверхности параллелепипеда. Объём параллелепипеда
45. Пирамида. Площадь её поверхности. Объём пирамиды
46. Усечённая пирамида. Площадь её поверхности. Объём усечённой пирамиды
47. Конус. Площадь поверхности конуса. Объём конуса
48. Усечённый конус. Площадь поверхности. Объём усечённого конуса
49. Цилиндр. Площадь поверхности цилиндра. Объём цилиндра
50. Сфера. Уравнение сферы
51. Шар. Его части. Площадь поверхности
52. Объём шара и его частей
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы:
а) Основные источники, в т.ч. из ЭБС:
1. Баврин И. И. Математика. Учебник и практикум для СПО / И. И. Баврин. — 2-е изд. испр. и доп. - Москва : Издательство Юрайт, 2017. – 616 с
2. Мордкович А.Г., Семенов П.В.Математика: алгебра и начала математического анализа, геометрия. 10-11 классы. Алгебра и начала математического анализа. В 2 ч. Ч. 1. Учебник для учащихся образовательных организаций (базовый уровень) / А.Г. Мордкович. – 3-е изд., стер. – М.: Мнемозина, 2015. – 448 с.
3. Мордкович А.Г., Семенов П.В.Математика: алгебра и начала математического анализа, геометрия. 10-11 классы. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся образовательных организаций (базовый уровень) / А.Г. Мордкович. – 3-е изд., стер. – М.: Мнемозина, 2015. – 271 с.
4. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы. Учебник для общеобразовательных организаций (базовый и углубленный уровни) / Л.С. Атанасян. – М.: Просвещение, 2017. – 256 с.
б) Дополнительная литература, в т.ч. из ЭБС:
1. Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — Москва : Юрайт, 2016. — 285 с
2. Богомолов, Н. В. Математика. Задачи с решениями в 2 ч. Часть 2 : учебное пособие для СПО / Н. В. Богомолов. — 2-е изд., испр. и доп. — Москва : Юрайт, 2016. — 285 с
3. Лисичкин, В.Т. Математика в задачах с решениями. [Электронный ресурс] : Учебные пособия / В.Т. Лисичкин, И.Л. Соловейчик. — Электрон.дан. — СПб. : Лань, 2014. — Режим доступа: http://e.lanbook.com/book/2785 — Загл. с экрана.
в) Ресурсы сети «Интернет»:
1. https://e.lanbook.com/ - Электронно-библиотечная система издательства Лань.
2. http://www.iprbookshop.ru/ - Электронно-библиотечная система IPRbooks.
3. https://www.biblio-online.ru/ - Электронная библиотека ЮРАЙТ.
4. http://znanium.com/ - Электронно-библиотечная система Znanium.com.
Приложение 1
Контрольная работа
по учебной дисциплине 00.00 Наименование
Обучающегося заочной формы обучения
специальности 000000
Наименование группы 00-000
Иванова Ивана Ивановича
Псков
2018
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по организации самостоятельной работы
и выполнению контрольной работы
по учебному предмету
ОУД.01 Математика: алгебра, начала анализа и геометрия
для обучающихся заочной формы обучения
специальности 23.02.03
Техническое обслуживание и ремонт автомобильного транспорта
Составитель: О.П. Проскурина
преподаватель Колледжа ПсковГУ
Псков
2018
Методические указания рассмотрены и рекомендованы к утверждению на заседании предметной цикловой комиссии ____________________________________________________________________________________________________________________________________
протокол №________ от «______» ____________ 20 г.
Председатель цикловой комиссии ________________ (Фамилия И.О.)
подпись
«________»_____________20 г.
СОДЕРЖАНИЕ
1. Пояснительная записка.
2. Методические указания к выполнению контрольной работы.
3. Варианты заданий для контрольной работы.
4. Экзаменационные вопросы.
5. Список рекомендуемой литературы.
6. Приложения.
Пояснительная записка
Рабочая программа учебного предмета “ Математика: алгебра, начала анализа и геометрия ” предназначена для реализации государственных требований к минимуму содержания и уровню подготовки выпускников заочного отделения по специальности СПО 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта» среднего профессионального образования.
Математика необходима для изучения программирования, математической статистики, математических методов и специальных дисциплин.
В методических указаниях приведены требования к основным знаниям и умениям, которые определяют обязательный минимальный уровень подготовки обучающихся по основному материалу.
Обучающиеся должны приобрести ряд общих знаний и навыков, необходимых для успешного усвоения математики, использования её при изучении специальных дисциплин, в курсовом и дипломном проектировании. Они должны уметь: делать ссылки на ранее изучаемый материал, самостоятельно изучать материал по учебной литературе, пользоваться справочными пособиями, предназначенными для средних специальных учебных заведений.
Обучающиеся должны усвоить, что математические понятия характеризуют свойства и отношения объектов реального мира, обладают широкой сферой применимости.
Дата: 2019-12-10, просмотров: 340.