В [2] описана методика расчета терминальных управлений в заданном классе функций. В соответствии с этой методикой управляющая функция с некоторыми неизвестными параметрами подается на вход управляемого объекта, структурная схема которого в простейшем случае может быть представлена в виде цепочки интеграторов. В результате последовательного интегрирования входной функции находится выражение для выходной функции, в которое войдут все неизвестные параметры входной функции. Из конченых условий, наложенных на выходную функцию, определяются значения неизвестных параметров управления. Очевидно, что решение будет однозначным, если число неизвестных параметров и число конечных условий равны.

При несложных структурных схемах объектов интегрирование с целью получения выражения для выходной функции не представляет труда и метод синтеза управлений достаточно прост. Однако на практике зачастую приходится иметь дело с довольно сложными объектами с нелинейностью в прямом и обратном каналах и внутренними обратными связями, замыкающимися не обязательно на вход системы. В этом случае получение выражения для выходной функции представляет собой значительную сложность. Для решения этой проблемы Батенко предложено выходную функцию не искать, а задавать. Вначале определяются из конечных условий ее неизвестные параметры, а затем, при движении по структурной схеме справа налево и последовательном дифференцировании выходной функции, получают управляющую функцию, приложенную к входу.

Предположим, что движение управляемого объекта r-го порядка описывается уравнением [2]

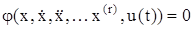.                                                           (3.10)

Его выходной функцией служит x(t), а управляющей u(t). Будем задавать желаемое движение объекта в классе непрерывных r раз дифференцируемых функций. Согласно теореме Вейерштрасса о приближении любая непрерывная функция может быть аппроксимирована полиномом с любой наперед заданной точностью. Поэтому в качестве функции, задающей требуемое движение, может быть выбран полином от времени следующего вида

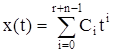,                                                                          (3.11)

который содержит r+n неизвестных параметров Ci. Здесь r – число начальных, а n–число конечных условий; из этих условий однозначно определяются параметры полинома (3.11).

Выбор полиномов в качестве класса функций, задающих требуемое движение объекта, имеет следующие преимущества. При любых линейных преобразованиях полином остается полиномом, изменяется только его степень. Его неизвестные параметры Ci определяются в результате решения алгебраических уравнений, кроме того, эти коэффициенты могут быть определены с помощью рекуррентных соотношений, приведенных ниже.

Рассмотрим вначале простейший класс управляемых объектов – цепочку интеграторов r-го порядка. Этот объект замечателен тем, что его фазовыми координатами служат выходная функция и r-1 ее производных. Все соотношения, которые будут получены для цепочки интеграторов, найдут применение и для объектов произвольной структуры.

Движение объекта, составленного из r последовательно включенных интеграторов, описывается следующей системой дифференциальных уравнений:

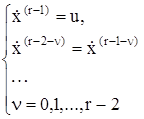.   (3.12)

Требуется найти такое управление u, которое переводит объект в течение времени Т из начального фазового состояния 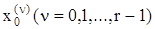в конечное, обеспечивая выполнение n конечных условий .

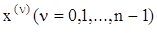Неизвестные параметры Ci выходной функции (3.11) находятся из граничных условий на левом (t = 0) и правом (t = T) концах фазовой траектории.

Последовательно дифференцируя выходную функцию (3.11), находим выражения для фазовых координат:

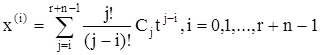.                                  (3.13)

Подставив в выражение (3.13) t = 0, из начальных условий определим первые r неизвестных параметров:

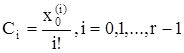,                                                             (3.14)

где 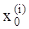 – начальные значения выходной функции и ее производных.

Остальные n параметров находятся решением системы уравнений (3.13), записанной для конечного момента времени t = T:

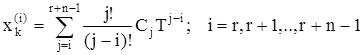. (3.15)

Для подсчета неизвестных параметров управления рекомендуется пользоваться рекуррентной формулой, боле приспособленной для машинной реализации:

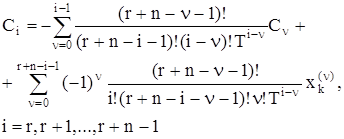.                             (3.16)

Первые r параметров Ci (i = 0,1, … , r-1), вычисляются по (3.14). Их значения входят в первое слагаемое (3.16).

Как было отмечено выше описанная методика синтеза терминального управления для систем, математическая модель которых может быть представлена в виде цепочки интеграторов. Далее будет рассмотрен метод, который позволяет синтезировать терминальные управления для линейных и нелинейных объектов произвольной структуры.

Данный метод носит название синтез терминальных управлений методом пересчета краевых условий. Основная идея метода состоит в следующем: краевые условия по внутренним фазовым координатам пересчитываются в краевые условия для выходной функции объекта. После этого синтез терминального управления производится в соответствии с методом, описанным выше.

Пусть движение объекта описывается системой дифференциальных уравнений

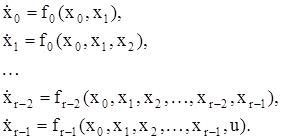.    (3.17)

Здесь r – порядок системы; 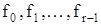 – непрерывные функции от фазовых координат; u – управляющая функция.

Требуется найти управление u(t), 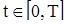, переводящее объект в течение заданного времени T из начального фазового состояния  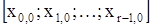в конечное, обеспечив при этом выполнение следующих граничных условий на правом конце фазовой траектории: 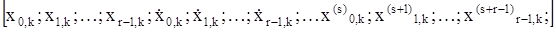. В конечный момент времени T необходимо обеспечить заданные значения r фазовым координатам и их производным, причем порядок производных s не ограничен.

Синтез управления начинается с задания выходной функции

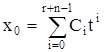.                                                                             (3.18)

Подставим (3.18) в первое уравнение системы (3.17), найдем из него

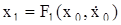.                                                                         (3.19)

Далее произведем подстановку (3.18) и (3.19) во второе уравнение системы (3.17), получим

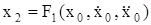. (3.20)

В результате r-1 последовательных подстановок найдем выражения всех внутренних фазовых координат объекта 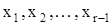 через выходную координату  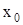и ее производные. Из последнего уравнения системы (3.17) находится управляющая функция

.                                                         (3.21)

Уравнения (3.19), (3.20) и им подобные для остальных фазовых координат дают связь между значениями внутренних фазовых координат 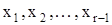 и выходной фазовой координатой  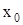и ее производными 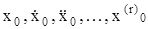. Поэтому найдем из этих уравнений выражения для производных выходной фазовой координаты через внутренние фазовые координаты:

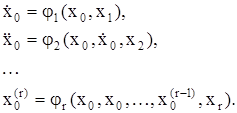.                                                  (3.22)

Переписывая (3.22) для начального (t = 0) и конечного моментов времени (t = T), получаем формулы для вычисления граничных значений производных выходной функции. Если найти такую управляющую функцию, которая обеспечит вычисленные по (3.22) граничные значения выходной функции и ее производных, то в силу однозначного соответствия этих значений граничным значениям внутренних фазовых координат будут также обеспечены и их краевые условия. Таким образом, выражения (3.22) служат для пересчета краевых условий по внутренним фазовым координатам на выход объекта. Параметры 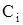 выходной функции (3.18), входящие также в управляющую функцию (3.21), вычисляются на основании пересчитанных на выход краевых условий по формулам (3.14) и (3.16).

В заключение обратим внимание на следующее. Пусть существует задача терминального управления всеми фазовыми координатами объекта r-го порядка с внутренними обратными связями. Граничные условия, наложенные на его фазовые координаты, однозначно определяют начальные и конечные значения выходной координаты r-1 ее производных. Поэтому свободно распоряжаться граничными значениями выходной функции, если это потребуется, можно только начиная с ее r-й производной и выше.

Таким образом, методика, описанная в данном разделе, является универсальной и может использоваться как для линейных, так и для нелинейных объектов. Ограничение применения данного подхода состоит в том, что входящие в систему нелинейности должны описываться аналитическими функциями. В этом слу­чае терминальное управление будет также аналитической функцией.