Определим функцию, которая возвращает 1, если ей передан аргумент 0;5, если аргумент был равен 1; 2, если аргумент равен 2 и -1 во всех остальных случаях. Используем операторcase:
f x= case x of
0 ->1
1 ->5
2 ->2
_ -> -1
Символ _ означает «во всех остальных случаях».
Вышеприведенную функцию можно записать и таким образом:
f x= case x of { 0-> 1; 1 -> 5; 2 -> 2; _ ->-1 }
Такой способ явно задает группировку и разделение конструкций языка. Однако можно использовать двумерную систему структурирования текста, которая позволяет обойтись без специальных символов группировки и разделения операторов.
Общее правило таково. После ключевых слов where, let, doиofинтерпретатор вставляет открывающую скобку «{» и запоминает колонку, в которой записана следующая команда. В дальнейшем перед каждой новой строкой, выровненной на запомненную величину, вставляется разделяющий символ «;». Если следующая строка выровнена меньше (т.е. ее первый символ находится левее запомненной позиции), вставляется закрывающая скобка. Поскольку в программе на языке HASKELL пробелы являются значимыми, необходимо при редактировании программ быть внимательными, особенно при использовании символов табуляции.
4.2.4. Кусочное задание функций
Функции могут быть определены кусочным образом. Это означает, что можно определить одну версию функции для определенных параметров и другую версию для других параметров. Так, функцию f из предыдущего раздела можно определить следующим образом:
f 0=1
f 1=5
f 2=2
f _= -1
Такой способ определения функций зачастую позволяет обойтись без операторов ifиcase. Так, функцию факториала можно определить в таком стиле:
factorial 0 = 1
factorial n = n * factorial (n -1)
4.2.5. Сопоставление с образцом
При определении рекурсивных функций на списках «базой рекурсии» будет пустой список ([]). Определим функцию вычисления длины списка, назовем ее lenи функцию конкатенации списков, назовем ее app:
len[] =0
len s =1+len(tail s)
app [] y= y
app x y =(head x) : app (tail x) y
Список, первым элементом которого (головой) является x, а остальные элементы (хвост) задаются списком xs, записывается как x:xs. Эту конструкцию можно применять и при описании функции:
len[] =0
len (x:xs) = 1 + len xs
app [] y= y
app (x:xs) y = x : app xs y
Такой прием называется сопоставление с образцом.
«Образцы», записываемые в аргументах функции, «сопоставляются» с переданными в нее фактическими параметрами. Если происходит сопоставление с образцом, упомянутые в нем переменные получают значения.
Функцию, принимающую на вход пару чисел и возвращающую их сумму, можно определить таким образом:
sum_pair p =fst p + snd p
Используя сопоставление с образцом, можно записывать такие функции следующим образом:
sum_pair (x,y) = x + y
sum_triple (x,y,z) = x + y + z
Если значения не нужны при вычислении функции, то, чтобы не вводить лишних имен, можно в образце использовать символ _. Он означает образец, который сопоставляется с любым значением, но не связывается с ним. Следующие примеры показывают различные варианты применения сопоставления с образцом:
--Функция суммирования двух первых элементов списка
f1 (x:y:xs) = x +y
--Определение функции, аналогичной head
my_head (x:xs) = x
--Определение функции, аналогичной tail.
my_tail (_:xs) = xs
--Функция извлечения первого элемента тройки
fst3 (x,_,_) = x
Сопоставление с образцом можно применять и в операторе case:
--Еще одно определение функции длины списка
my_length s = case s of
[] ->0
(_:xs) -> 1 + my_length xs
Определим функцию, принимающую список пар чисел и возвращающую сумму их разностей:
f[] =0
f ((x,y):xs) = (x -y) + f xs
Функция, вычисляющая квадраты элементов списка чисел, может быть определена следующим образом:
square [] = []
square (x:xs) = x*x : square xs
4.2.6. let-связывание
При определении функций часто бывает необходимо использовать некоторые временные переменные для хранения промежуточных результатов. Можно записать следующую функцию для вычисления пары корней квадратного уравнения ax2+ bx +c = 0:
roots a b с =
((-b + sqrt (b*b - 4*а*с)) / (2*а), (-b - sqrt (b*b - 4*а*с)) / (2*а))
Недостатки такой записи очевидны. С использованием локальных переменных эту функцию можно записать так:
roots a b с =
let det = sqrt (b*b - 4*a*c)
in ((-b + det / (2*a),(-b - det / (2*a))
Локальная переменная det доступна только в определении функции roots. Можно определять несколько локальных переменных:
roots a b с =
let det = sqrt (b*b - 4*a*c)
twice_a = 2*a
in ((-b + det) / twice_a, (-b - det) / twice_a)
В конструкции let ... in ... используется правило выравнивания: первый символ, отличный от пробела, следующий за ключевым словом let, задает колонку, относительно которой должны выравниваться последующие определения. С использованием символов «{», «}» и «;» правило выравнивания становится необязательным, и функцию roots можно было бы записать так:
roots a b с =
let { let = sqrt (b*b - 4*a*c); twice_a = 2*a }
in ((-b + det) / twice_a, (-b - det) / twice_a)
Помимо конструкции let ... in ... иногда удобнее использовать конструкцию ... where ... , в которой определения локальных переменных следуют после основной функции:
roots a b с = ((-b + det) / twice.a, (-b - det) / twice_a)
where det = sqrt (b*b - 4*a*c)
twice_a = 2*a
Если мы вместо локальных переменных используем глобальные функции, например:
det a b c= sqrt (b*b - 4*а*с)
twice_a a = 2*а
roots a b с =
((-b + det a b с) / twice_a a, (-b - det a b с) / twice_a a),
то, во-первых, мы вводим вспомогательные функции в глобальном пространстве имен (а это значит, что мы теперь не сможем использовать их для других полезных функций), во-вторых, для вычисления этих функцийнужно передавать соответствующие параметры, тогда как локальные определения могут свободно использовать параметры функции, в рамках которой они определены.
В конструкциях let и where можно определять не только переменные, но и функции. Рассмотрим, например, функцию, возвращающую по заданному числу n список натуральных чисел [1,2,...,n]. Введем вспомогательную функцию numsFrom, которая по заданному числу m возвращает список [m,m+l,m+2,...,n] и сделаем его определение локальным:
numsTo n =
let numsFrom m = if m == n then [m] else m:numsFrom (m + 1)
In numsFrom 1
Функция numsFrom использует в своем определении переменную n, хотя она не передается в нее в качестве параметра.
4.2.7. Охраняющие условия
Определяемые нами функции могут не вычисляться при некоторых значениях аргумента. Например, функция факториал работает, если мы не попытаемся вычислить факториал отрицательного числа. В этом случае вычисление уходит в бесконечную рекурсию.
Простейший способ сигнализировать о таких ошибках — использовать стандартную функцию error. Она принимает в качестве аргумента строку, а ее вычисление приводит к остановке программы и выдаче на экран этой строки. Таким образом, функцию факториала запишем так:
factorial 0=1
factorial n = if n > 0 then n * factorial (n - 1) else
error "factorial: negative argument"
С помощью сопоставления с образцом можно выделить структуру переданных в функцию параметров и равенство элементов этих параметров константным значениям. Однако зачастую необходимо накладывать более сложные ограничения на входные параметры.
Использование охраняющих условий позволяет записать функцию факториала следующим более лаконичным образом:
factorial 0=1
factorial n | n < 0 = error "factorial: negative argument"
| n >= 0 = n * factorial (n - 1)
Вместо последнего условия можно использовать слово otherwise. Например, функция signum выглядит следующим образом:
signum х | х < 0 = -1
| х == 0 =0
| otherwise = 1
Определение функций в таком стиле обычно нагляднее, чем при традиционном использовании условного выражения.
4.2.8. Полиморфизм
Полиморфная система типов означает, что в языке присутствуют типовые переменные. Рассмотрим уже известную нам функцию tail. Она одинаково применима и к списку целых, и к списку символов, и к списку строк:
Prelude>tail [1,2,3]
[2,3]
Prelude>tail ['a','b','с']
['b'.'с']
Prelude>tail ["list", "of", "lists"]
["of", "lists"]
Функция tail имеет полиморфныйтип: [а] -> [a]. Это означает, что она принимает в качестве аргумента любой список и возвращает список того же самого типа. Здесь, а обозначает типовую переменную, т.е. подразумевается, что вместо нее можно подставить любой конкретный тип. Таким образом, запись [а] -> [а] задает целое семейство типов, представителями которого являются, например [Integer] -> [Integer], [Char] -> [Char], [[Char]] -> [[Char]]и т.п.
Аналогично функция head, возвращающая первый элемент списка, имеет тип [а] -> а. Представителями этого семейства являются типы [Integer] -> Integer, [Char] -> Char и т.п.
Многие функции, работающие со списками, парами и кортежами, имеют полиморфные типы. Так, функция fst имеет тип (а, b)->а (в определении этого типа используются две типовые переменные).
4.3. Пользовательские типы
Помимо использования стандартных типов, программисту предоставлена возможность, определять свои собственные, специфические типы данных. Для этого используется ключевое слово data.
4.3.1. Синонимы типов
В языке есть возможность определения синонимов типов, т. е. имен для часто используемых типов. Они создаются с помощью ключевого слово type. Вот несколько примеров:
type String = [Char]
type Person = (Name, Address)
type Name = String
type Address = Maybe String
Синонимы типов не определяют новых типов, а просто дают новые имена для уже существующих типов. Например, тип Person->Name полностью эквивалентен типу (String,Maybe String) -> String. Однако их используют, поскольку, во-первых, они помогают дать более короткие имена типам, а во-вторых, повышают уровень понятности кода.
4.3.2. Пары
Для примера рассмотрим определение пары, очень похожей на стандартную:
data Pair a b = Pair a b
Здесь ключевое слово data показывает, что мы собираемся определять тип данных, Pair- название этого типа, а и b являются типовыми переменными, обозначающими параметры типа. Таким образом, мы определяем структуру данных, параметризованную двумя типами а и b. После знака равенства мы указываем конструкторы данных этого типа - Pair. (имя конструктора данных не обязательно должно совпадать с именем типа). После имени конструктора данных мы снова пишем: а b, что означает, что для того, чтобы сконструировать пару, нам нужно два значения: одно, принадлежащее типу а и другое - типу b.
Это определение вводит функцию Pair :: а -> b -> Pair a b, которая используется для конструирования пар типа Pair. Загрузив этот код в интерпретатор, можно посмотреть, как конструируются пары:
Main>:t Pair
Pair :: а -> b -> Pair a b
Main>:t Pair 'a'
Pair 'a' :: b -> Pair Char b
Main>:t Pair 'a' "Hello"
Pair 'a' "Hello" :: Pair Char [Char]
Функции, соответствующие конструкторам данных, обладают тем свойством, что их можно использовать при сопоставлении с образцом. Так, функции для получения первого и второго элемента нашей пары можно определить следующим образом:
pairFst (Pair х у) = х
pairSnd (Pair x у) = у
С использованием типа Pair можно определить набор функций, работающих только с этим типом и отделить их от функций, работающих с парами «вообще». Можно определить некоторые ограничения на получаемые пары, которых невозможно добиться с помощью стандартного типа. Например, если нам нужен тип, хранящий пару элементов одного и того же типа. Его можно определить так:
data SamePair a = SamePair a a
Здесь тип имеет один параметр, однако конструктор данных принимает два параметра одного и того же типа.
4.3.3. Множественные конструкторы
В предыдущем примере мы рассматривали тип данных с единственным конструктором. Возможно (и зачастую очень полезно) определить тип с несколькими конструкторами. Конструкторы отделяются друг от друга символом «|».
Рассмотрим тип Color, представляющий цвет, с возможными значениями Red, Green и Blue. Его можно определить так:
data Color = Red | Green | Blue
Здесь Color — название типа, a Red, GreenиBlue — конструкторы данных. Заметьте, что этот тип не принимает параметров. Такие типы называются перечислимыми. Другой пример, стандартный тип Bool определен таким образом:
data Bool = True | False
Множественные конструкторы могут также принимать параметры. Расширим наш тип Color так, чтобы он позволял определять произвольный цвет, задаваемый тремя целыми числами, соответствующим уровням красного, зеленого и синего (стандартное rgb-представление):
data Color = Red | Green | Blue | RGB Int Int Int
Здесь тип Color, помимо стандартных цветов, позволяет определять произвольный цвет с помощью конструктора RGB, принимающего числовые rgb-компоненты цвета. Тогда, например, функция для выделения red-компоненты цвета запишется так:
redComponent :: Color -> Int
redComponent Red = 255
redComponent (RGB r _ _) = r
redComponent _ = 0
Типы с множественными конструкторами также могут быть полиморфными. Пусть функция должна вернуть некоторый результат, либо сообщить об ошибке. Например, функция для решения линейного уравнения возвращает найденный корень; функция для поиска первого неотрицательного числа в списке возвращает это число и т.п. Вместе с тем решение уравнения может не существовать, в списке не оказаться неотрицательных чисел и т.д. Как сообщить об этом тому, кто вызвал функцию? Иногда (как в случае получения неотрицательного элемента) можно ввести договоренность, что возврат какого-либо специального значения (например, -1) означает «нет результата». Однако это не всегда возможно: в случае решения линейного уравнения такого выделенного значения не существует. Проблема решается с помощью стандартного типа Maybe, определенного так:
data Maybe a = Nothing | Just a
Тип Maybe параметризован типовой переменной а и предоставляет два конструктора: Nothing для представления отсутствия результата и Just для осмысленного результата. Тогда наши функции можно записать так:
-- Корень уравнения ах + b = О
solve :: Double -> Double -> Maybe Double
solve 0 b = Nothing
solve a b = Just (-b / a)
-- Первый положительный элемент списка
findPositive :: [Integer] -> Maybe Integer
findPositive [] = Nothing
findPositive (x:xs) | x > 0 = Just x
| otherwise = findPositive xs
Использование типа Maybe обладает рядом преимуществ. Его использование явно показывает, что функция может возвратить «отсутствие результата». В случае выделенного значения для того, чтобы узнать, как функция сообщает об этом, необходимо изучить документацию к функции. С Maybe эта информация содержится в типе функции и ее может предоставить сам интерпретатор. Более того, при обработке возвращаемого значения функции необходимо явно сделать сопоставление с образцом, и если мы забудем обработать случай с Nothing, компилятор может выдать предупреждение.
4.3.4. Классы типов
Класс типов представляет собой некоторое множество типов, обладающих рядом общих свойств. Например, в класс типов Eq входят те типы, для объектов которых определено отношение равенства, т.е., если переменные х и у принадлежат одному и тому же типу, входящему в класс Eq, мы можем вычислять выражения х == у и х /= у. Все простые типы, а также списки и кортежи входят в этот класс, однако, например, для функции отношение равенства не определено и типы функций не принадлежат классу Eq.
Другим важным классом является класс Show.В него входят те типы, объекты которых могут быть преобразованы в строку для того, чтобы возможно было отобразить на экране. Простые типы, кортежи и списки входят в этот класс, поэтому интерпретатор может их напечатать. Функции не входят в этот класс.
По умолчанию пользовательские типы не входят ни в какой класс, поэтому значения этих типов нельзя сравнивать и интерпретатор не может напечатать их. Это, разумеется, неудобно. Поэтому можно при определении типов задать их принадлежность желаемым классам. Для этого после определения типа необходимо добавить ключевое слово deriving и в скобках перечислить классы, к которым должен принадлежать тип. Пример:
-- Тип, представляющий время дня
data DayTime = Morning | Afternoon
| Evening | Night deriving (Eq, Show)
Желательно при определении типов относить их к классам Eq и Show. Это существенно облегчает работу.
4.4. Рекурсивные типы
При определении типов данных в правой части определения можно использовать определяемый этой конструкцией тип. Это дает возможность определять рекурсивные структуры данных. Одной из основных таких структур является дерево.
Определим бинарное дерево, в листьях которого находятся элементы типа a, следующим образом:
data Tree a = Leaf a | Branch (Tree a) (Tree a)
Это определение говорит, что дерево (Tree) является либо листом (Leaf), либо ветвью (Branch), у которого есть левое и правое поддерево. В приведенном определении Leaf и Branch — конструкторы данных, а Tree a, встречается и в левой, и в правой части определения - название типа.
Работа с рекурсивными типами практически не отличается от работы с обычными типами, за тем исключением, что практически все функции, работающие с рекурсивными типами, сами также рекурсивны.
Например, определим функцию treeSize, возвращающую количество листьев в дереве. Она записывается следующим образом:
treeSize (Leaf _) = 1
treeSize (Branch l r) = treeSize l + treeSize r
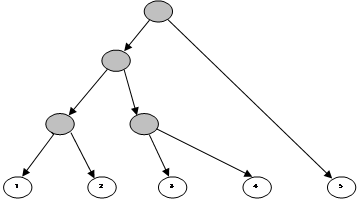
Применение этой функции для данного дерева выглядит следующим образом:
Main>treeSize (Branch (Branch (Branch (Leaf 1) (Leaf 2)) (Branch (Leaf 3) (Leaf 4)) (Leaf 5))
Другим примером функции для работы с деревьями служит функция для получения списка всех листьев дерева:
leafList (Leaf x) = [x]
leafList (Branch left right) = leafList left ++ leafList right
Применим ее для данного дерева:
Main>leafList (Branch (Branch (Branch (Leaf 1) (Leaf 2)) (Branch (Leaf 3) (Leaf 4)) (Leaf 5))
[1,2,3,4,5]
4.4.1. Списки как рекурсивные типы
Список также является рекурсивным типом. Рассмотрим следующий полиморфный тип:
data List a = Nil | Cons a (List a)
Значение типа List a либо пусто (Nil), либо содержит элемент типа a и значение типа List a. Нетрудно заметить прямую аналогию со списками, которые также либо пусты ([]), либо содержат голову типа a и хвост, являющийся также списком. Конструктор Cons можно записать в инфиксном виде:
data List a = Nil | a ‘Cons‘ (List a)
Для значений типа List можно определить все функции, определенные для списков. Приведем примеры функций headиtail:
headList (Cons x _) = x
headList Nil = error "headList: empty list"
tailList (Cons _ y) = y
tailList Nil = error "tailList: empty list"
Проиллюстрируем работу этих функций:
Main>headList (Cons 1 (Cons 2 Nil))
Main>tailList (Cons 1 (Cons 2 Nil))
Cons 2 Nil
4.4.2. Синтаксические деревья
Деревья широко используются в программировании. Например, результатом грамматического разбора программы в любом компиляторе является синтаксическое дерево. Приведем пример такого дерева для выражений, содержащих константы, символы сложения и умножения:
data Expr = Const Integer | Add Expr Expr | Mult Expr Expr
Из этого определения видно, что выражение (Expr) является либо целочисленной константой (Const), либо суммой или произведением двух выражений. Например, для выражения 1+2∗(3+4) соответствующее значение типа Expr имеет вид:
Дата: 2016-10-02, просмотров: 411.