WORDING MATHEMATICAL SIGNS, SYMBOLS AND FORMULAE
Поможем в ✍️ написании учебной работы

| Plus |
| - | Minus |

| plus or minus |

| sign of multiplication; multiplication sign |
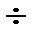
| sign of division; division sign |

| round brackets; parentheses |

| Curly brackets; braces |

| square brackets; brackets |

| Therefore |

| approaches; is approximately equal |
| ~ | equivalent, similar; of the order of |

| is congruent to; is isomorphic to |

| a equal b; a is equal to b |

| a is not equal to b; a is not b |
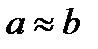
| approximately equals b |

| a plus or minus b |

| a is greater than b |
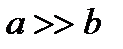
| a is substantially greater than b |

| a is less than b |
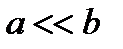
| a is substantially less than b |

| a second is greater than a d-th |

| x approaches infinity x tends to infinity |

| a is greater than or equals b |

| p is identically equal to q |

| n factorial |

| Laplacian |

| a prime |

| a double prime; a second prime |
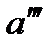
| a triple prime |

| a vector; the mean value of a |

| the first derivative |
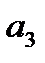
| a third; a sub three; a suffix three |

| a j th; a sub j product |

| f prime sub (suffix) c; f suffix (sub) c, prime |

| a second, double prime; a double prime, second |

| eighty seven degrees six minutes ten second |

| a plus b is c; a plus b equals c; a plus b is equal to c; a plus b makes c |

| a plus b all squared |

| c minus b is a; c minus b equals a; c minus b is equal to a; c minus b leaves a |
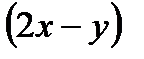
| bracket two x minus y close the bracket |

| a time b is c; a multiplied by b equals c; a by b is equal to c |

| a is equal to the ratio of e to l |
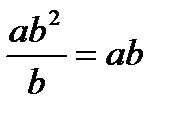
| ab squared (divided) by b equals ab |
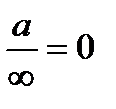
| a divided by infinity is infinity small; a by infinity is equal to zero |

| x plus or minus square root of x square minus y square all over y |

| a divided by b is c; a by b equals c; a by b is equal to c; the ratio of a to b is c |

| a to b is as c to d |

| a (one) half |
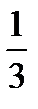
| a (one) third |
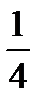
| a (one) quarter; a (one) fourth |
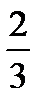
| two thirds |

| twenty five fifty sevenths |
2 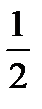
| two and a half |
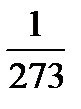
| one two hundred and seventy third |

| o [ou] point five; zero point five; nought point five; point five; one half |

| o [ou] point five noughts one |

| the cube root of twenty seven is three |
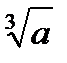
| the cube root of a |

| the fourth root of sixteen is two |

| the fifth root of a square |

| Alpha equals the square root of capital R square plus x square |

| the square root of b first plus capital A divided by two xa double prime |

| a) dz over dx b) the first derivative of z with respect to x |
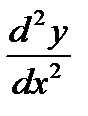
| a) the second derivative of y with respect to x b) d two y over d x square |

| the nth derivative of y with respect to x |

| partial d two z over partial d  square plus partial d two z over partial d square plus partial d two z over partial d 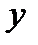 square equals zero square equals zero
|

| y is a function of x |
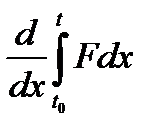
| d over dx of the integral from t nought to t of capital F dx |
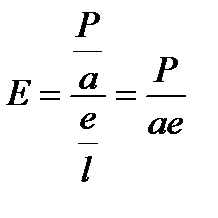
| capital E is equal to the ratio of capital P divided by a to e divided by l is equal to the ratio of the product Pl to the product ae |

| capital L equals the square root out of capital R square plus minus 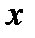 square square
|

| gamma is equal to the ratio of c prime c to ac prime |

| a to the m by nth power equals the nth root of (out of) a to the mth power |

| the integral of dy divided by the square root out of c square minus y square |

| capital F equals capital C sub (suffix) mu HIL sine theta |

| a plus b over a minus b is equal to c plus d over c minus d |

| capital V equals u square root of sine square i plus cosine square i equals u |

| tangent r equals tangent i divided by l |

| the decimal logarithm of ten equals one |

| a cubed is equal to the logarithm of d to the base c |

| four c plus W third plus two n first a prime plus capital R nth equals thirty three and one third |

| capital P sub (suffix) cr (critical) equals  square capital El all over four l square square capital El all over four l square
|

| x + a is round brackets to the power p minus the r-th root of x all (in square brackets) to the minus q-th power minus s equals zero |

| Open round brackets capital D minus r first close the round brackets open square and round brackets capital D minus r second close round brackets by y close square brackets equals open round brackets capital D minus r second close the round brackets open square and round brackets capital D minus r first close round brackets by y close square brackets |

| u is equal to the integral of f sub one of x multiplied by dx plus the integral of f sub two of y multiplied by dy |

| capital M is equal to capital R sub one multiplied by x minus capital P sub one round brackets opened x minus a sub one brackets closed minus capital P sub two round brackets opened x minus a sub two brackets closed |

| a sub v is equal to m omega omega square alpha square divided by square brackets, r, p square m square plus capital R second round brackets opened capital R first plus omega square alpha square divided by rp round and square brackets closed |

| a)  of z is equal to b, square brackets, parenthesis, z divided by c sub m plus 2, close parenthesis to the power m over m minus 1, minus 1, close square brackets; b) of z is equal to b, square brackets, parenthesis, z divided by c sub m plus 2, close parenthesis to the power m over m minus 1, minus 1, close square brackets; b)  of z is equal to b multiplied by the whole quantity; the quantity 2 plus z over c sub m, to the power m over m minus 1, minus 1 of z is equal to b multiplied by the whole quantity; the quantity 2 plus z over c sub m, to the power m over m minus 1, minus 1
|
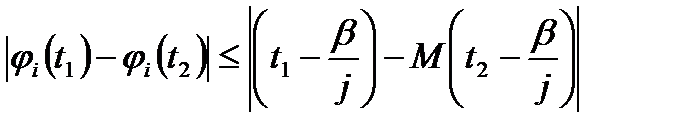
| the absolute value of the quantity  sub j of t one minus sub j of t one minus  sub j of t two is less than or equal to the absolute value of the quantity M of t one minus sub j of t two is less than or equal to the absolute value of the quantity M of t one minus  over j, minus M of over j, minus M of  sub 2 minus sub 2 minus  over j over j
|

| the limit as s becomes infinite of the integral of f of s and 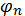 of s plus delta n of s, with respect to s, from of s plus delta n of s, with respect to s, from  to t, is equal to the integral of f of s and to t, is equal to the integral of f of s and  of s, with respect to s, from of s, with respect to s, from  to t to t
|
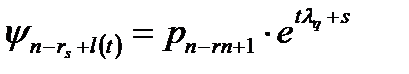
|  sub n minus r sub s plus l of t is equal to p sub n minus r
sub s plus l, times e to the power of t times sub n minus r sub s plus l of t is equal to p sub n minus r
sub s plus l, times e to the power of t times  sub q plus s sub q plus s
|

| the partial derivative of F of lambda sub i of t and t, with respect to lambda, multiplied by lambda sub i prime of t, plus the partial derivative of F with arguments lambda sub i of t and t, with respect to t, is equal to zero |

| the second derivative of y with respect to s, plus y, times the quantity 1 plus b of s, is equal to zero |
 
| f of z is equal to  sub mk hat, plus big 0 of one over the absolute value of z, as absolute z becomes
infinite, with the argument of z equal to gamma sub mk hat, plus big 0 of one over the absolute value of z, as absolute z becomes
infinite, with the argument of z equal to gamma
|

| D sub n minus 1 of  is equal to the product from s equal to zero to n of, parenthesis, 1 minus x sub s squared, close parenthesis, to the power epsilon minus 1 is equal to the product from s equal to zero to n of, parenthesis, 1 minus x sub s squared, close parenthesis, to the power epsilon minus 1
|
 
| the second partial (derivative) of u with respect to t plus a to the fourth power, times u, is equal to zero, where a is positive |

| set of functions holomorphic in D (function spaces) |
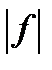
| Norm of f, the absolute value of f |

| distance between the sets  and and  (curves, domains, regions) (curves, domains, regions)
|

| b is the imaginary part of a + bi (complex variables) |
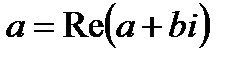
| a is the real part of a + bi (complex variables) |
| ∂S | the boundary of S |
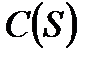
| the complement of S |

| union of sets C and D |

| intersection of sets C and D |

| B is a subset of A; B is included in A |

| a is an element of the set A; a belongs to A |
ANSWER KEYS
PART I
Unit 1
Reading and Vocabulary
| 1. | 1c | 2b | 3a | 4g | 5f | 6d | 7e |
| 2. | 1b | 2a | 3g | 4f | 5c | 6d | 7e |
3. 1 to apply, 2 to be admitted, 3 to take/to pass an exam, 4 to attend, 5 to miss, 6 to do research, 7 Bachelor’s degree
Grammar focus
| A | 1. How old is s/he? 2. Where does s/he come from? 3. Did he/she pass entrance exams? 4. What were his/her external scores? 5. What faculty does s/he study at? 6. What course does s/he take? 7. What subjects does s/he study? 8. Does s/he live in a dormitory? 9. What is s/he going to do after his/her Bachelor’s degree? |
Дата: 2016-10-02, просмотров: 379.