Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

4.1. Способ цепной подстановки

4.2. Способ абсолютных разниц

4.3. Способ относительных разниц

4.4. Индексный метод

4.5. Способ пропорционального деления и долевого участия.

4.6. Интегральный способ

4.7. Способ логарифмирования

Способ цепной подстановки.

 

Это наиболее универсальный способ, так используется для всех видов детерминированных моделей: аддитивных, мультипликативных, кратных и смешанных. Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать (исключить) влияние всех факторов, кроме одного, и определить воздействие последнего на прирост ре­зультативного показателя.

Математическое описание способа цепных подстановок при использовании его на примере четырехфакторной мультипликативной зависимости выглядит следующим образом:

у₀ = a₀*b₀*c₀*d₀,

у₁ = a₁*b₁*c₁*d₁,

где у₀ - величина результирующего показателя базисного периода,

у₁ – величина результирующего показателя фактического отчетного периода,

a₀,b₀,c₀,d₀, - факторы влияющие на результативный показатель.

 

Последовательные подстановки имеют следующие зависимости:

Уусл¹ = a₁*b₀*c₀*d₀,

Уусл² = a₁*b₁*c₀*d₀,

Уусл³ = a₁*b₁*c₁*d₀,

 

Расчет влияния каждого фактора на результирующий показатель вычисляется следующим образом:

Δу^а = Уусл¹ – У₀,

Δу^b = Уусл² – Уусл¹,

Δу^c = Уусл³ – Уусл²,

Δу^d = У¹ – Уусл³,

Баланс отклонений имеет вид:

Δу= y₁ – y₀ = Δу^а + Δу^b + Δу^c + Δу^d .

 

Используя способ цепной подстановки, необходимо помнить:

1. В первую очередь нужно учитывать изменение количественных, а затем качественных показателей.

2. Количество условных показателей на один меньше, чем число факторов.

Для многофакторных моделей чаще всего применяется прием прямого счета с использованием аналитических таблиц. Для реализации этого приема строится специальная аналитическая таблица. Рассмотрим макет таблицы для четырехфакторной модели y = f(a,b,c,d) (табл. 4.1).

 

 

Таблица 4.1. – Расчет влияния факторов на изменение результативного показателя методом прямого счета

Подстановки	Взаимодействующие факторы	Результативный показатель	Влияние фактора
a	b	c	d
1. Базовые значения факторов	ao	bo	co	do		Х
2. Изменение фактора а	ai	bo	co	do
3. Изменение фактора b	ai	bi	co	do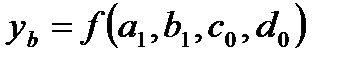
4. Изменение фактора c	ai	bi	ci	do
5. Изменение фактора d	ai	bi	ci	di
Совокупное влияние факторов	x	x	x	x	Х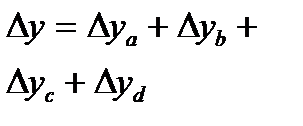

Способ абсолютных разниц

Способ абсолютных разниц применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях и моделях мультипликативно-аддитивного типа: Y= (а - b)с.

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Порядок аналитических расчетов на четырехфакторной мультипликативной зависимости выглядит следующим образом.

у₀ = a₀*b₀*c₀*d₀,

у₁ = a₁*b₁*c₁*d₁,

где у₀ - величина результирующего показателя базисного периода,

у₁ – величина результирующего показателя фактического отчетного периода,

a₀,b₀,c₀,d₀, - факторы влияющие на результативный показатель.

Расчеты влияния исследуемых факторов представляют следующую зависимость:

ΔУ^a = Δa₁*b₀*c₀*d₀,

ΔУ^b = a₁* Δb*c₀*d₀,

ΔУ^c = a₁*b₁ *Δc *d₀,

ΔУ^d = a₁*b₁*c₁ *Δd.

Баланс отклонений имеет вид:

Δу= у₁ – у₀ = Δу^а + Δу^b + Δу^c + Δу^d .

 

С помощью способа абсолютных разниц получаются те же результаты, что и способом цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов равнялась его общему приросту.

Способ относительных разниц

Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных моделях. Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов. Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y = abc.

Изменение результативного показателя определяется следующим образом:

Δy_a = y₀* Δa%,

Δy_b = (y₀+y_a) * Δb%,

Δy_c =( y₀+ y_a+y_b)* Δc%,

где,

Δa% = (a₁-a₀)/ a₀,

Δb% = (b₁-b₀)/ b₀,

Δc% = (c₁-c₀)/ c₀,

Для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в виде десятичной дроби.

Чтобы рассчитать влияние второго фактора, нужно к плановой (базисной) величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора.

Влияние третьего фактора определяется аналогично: к плановой величине результативного показателя необходимо прибавить его при­рост за счет первого и второго факторов и полученную сумму умно­жить на относительный прирост третьего фактора и т.д.

Данный способ удобно применять когда требуется рассчитывать влияние большого комплекса факторов (8—10 и более). В отличие от предыдущих способов здесь значительно сокращается число вычислительных процедур, что обусловливает его преимущество.

 

Индексный метод

 

Индексный метод основывается на относительных показателях, выражающих отношение уровня данного явления к уровню его в прошлое время или к уровню аналогичного явления, принятому в качестве базы. Всякий индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений – групповыми.

Индексным методом можно выявить влияние на изучаемый совокупный показатель различных факторов. Статистика называет несколько форм индексов, которые используются в аналитической работе (агрегатная, арифметическая, гармоническая и др.)

Важным составным элементом индекса является его вес или коэффициент сведения частей разнородной совокупности к единому показателю. Он должен сохранить модель структуры изучаемого явления в динамики.

Принято при исчислении объемных индексов в качестве веса использовать цены (р_о), а при исчислении индексов качественных показателей – объемы (q₁).

Основной формой экономического индекса является агрегатный, характеризующий изменение уровня развития всей сложной совокупности.

С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Исчисляют агрегатный индекс по формулам:

Индекс объемов:

I_q = ∑q₁ p₀ ,

∑q₀ p₀

 

Индекс качеств I_р = ∑q₁ p₁ , (цены)

∑q₁ p₀

 

Индекс оборотов I_о = ∑q₁ p₁ = I_q * I_р

∑q₀ p₀

 

где р₁, р₀ – цена отчетного и базисного периода

q₁, q₀ - количество в отчетном и базисном периоде.

 

Суть индексного метода состоит в использовании в анализе специальных индексов и сформированных статистических индексов в зависимости от цели анализа.

В зависимости от сроков исчисления различают базисные и цепные индексы. При базисных индексах за базу сравнения принимается показатель одного года (постоянная величина). Когда за базис для каждого последующего периода принимается показатель предыдущего периода (переменная величина), называется цепным.

Описанные выше четыре способа основаны на методе элиминирование, исключения воздействия всех факторов на результативный показатель, кроме одного.