Зубчатая передача является механизмом, который посредством зубчатого зацепления передает или преобразует вращательное движение с изменением скоростей и усилий, а иногда видов движения (поступательное во вращательное и наоборот).
Зубчатые передачи составляют самую распространенную и многочисленную группу механических передач. Они применяются в приводах различных приборов, машин и технологического оборудования для передачи окружных сил от долей грамма (часы, приборы и т.д.) до тысяч тонн (подъемные мосты, турбины, строительные машины и др.), с диаметрами зубчатых колес от долей миллиметра до 10 метров. Диапазон передаваемых мощностей – от долей ватта до десятков тысяч киловатт.
Зубчатые передачи в сравнении с другими механическими передачами обладают существенными достоинствами, а именно:
а) относительно малыми габаритами;
б) высоким КПД – η(0,96…0,98);
в) большой надежностью и долговечностью (до 70…80 тысяч часов работы);
г) возможностью использования в различных конструкциях в широком диапазоне размеров, скоростей, усилий и мощностей;
д) постоянством передаточного числа из-за отсутствия проскальзывания.
К основному недостатку зубчатых передач можно отнести повышенный шум при значительных скоростях и неточном монтаже.
Зубчатые передачи применяются для передачи вращательного движения между валами с параллельными, пересекающимися и перекрещивающимися осями, а также для преобразования вращательного движения в поступательное и наоборот. На кинематических схемах зубчатых механизмов такие передачи изображаются простыми геометрическими фигурами (окружности, прямоугольники, трапеции), симметрично расположенными на их осях вращения с обозначением способа закрепления (знак «Х» – для неподвижного соединения вала с зубчатым колесом). Часто на схемах передач тремя различными линиями на геометрических фигурах показываются виды зубьев: (прямые  , косые
, косые  , шевронные
, шевронные  , круговые
, круговые  , криволинейные
, криволинейные  ).
).
Зубчатые передачи между валами с параллельными осями осуществляются цилиндрическими зубчатыми колесами с:
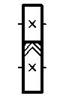
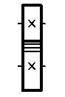
Условное обозначение
на кинематической схеме
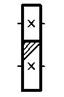
Ø прямыми зубьями
Ø косыми зубьями
Ø шевронными зубьями
Зубчатые передачи между валами с пересекающимися осями осуществляются коническими зубчатыми колесами с:
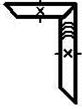
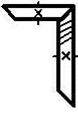
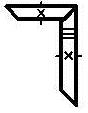
Ø прямыми зубьями
Ø круговыми зубьями
Ø косыми зубьями
Зубчатые передачи между валами с перекрещивающимися осями осуществляются зубчато-винтовыми колесами.
Краткие сведения из геометрии
и кинематики эвольвентных зацеплений
При проектировании, изготовлении и применении зубчатых передач важное значение имеет профиль зубьев зубчатых колес, который для передачи вращательного движения зацеплением, вообще говоря, может быть выбран произвольно (от окружности до прямой линии). Наиболее распространенным является эвольвентный профиль зубьев, предложенный Эйлером в 1760 г., который может быть нарезан простым зуборезным инструментом независимо от числа и вида зубьев, одинаковым для шестерни и колеса. Кроме того, эвольвентное зацепление малочувствительно к отклонению межосевого расстояния, что позволяет осуществлять корригирование (исправление профиля с целью улучшения работы зубьев при их контакте). Наиболее конкурентным (а в ряде случаев – предпочтительным) эвольвентному зацеплению является зацепление Новикова с двумя линиями зацепления, предложенное М.Л. Новиковым в 1955 г. При несомненных достоинствах последнего зубья с этим зацеплением можно нарезать только в косозубых (кругловинтовых) зубчатых передачах, исключая широкий класс прямозубых передач с внешним и внутренним зацеплением.
На рис. 5 показаны основные параметры некорригированного внешнего зубчатого зацепления быстроходной передачи редуктора, ниже приведены их геометрические соотношения. Здесь параметрам шестерни соответствует индекс «1», параметрам колеса – индекс «2». В силовых передачах шестерня – ведущий орган передачи – всегда меньшего диаметра.
1. Шаг зацепленияP – расстояние между одноименными поверхностями двух соседних (смежных) зубьев, измеренное по дуге делительной окружности. У косозубых передач различают 2 шага: нормальный шаг Pn, измеренный в плоскости, перпендикулярной линии зуба (нормальной плоскости), и окружной (делительный) шаг Pt, измеренный в торцевой плоскости зубчатого колеса (см. рис. 5). Нормальный шаг удобен в измерении при изготовлении, окружной шаг применяется в расчетах. Их соотношение:
Pn = Pt × cos β,
где β – угол наклона зубьев.
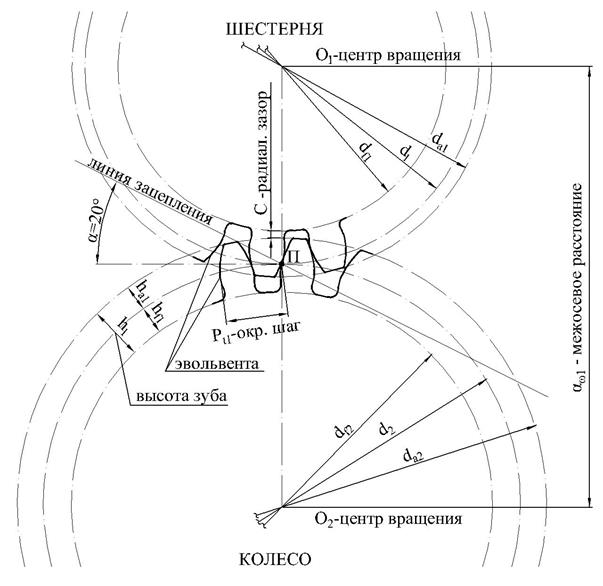
Рис. 5. Основные геометрические параметры
быстроходной зубчатой передачи
Окружной шаг Pt определяется из равноценных соотношений длины делительной окружности, т.е. πd = Z × Pt, откуда Pt = π 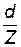 .
.
2. Число зубьев шестерни Z1 и колеса Z2. В силовых (понижающих) передачах всегда Z1<Z2.
У некорригированных зубчатых колес всегда Z1 > 17, Z2 < 170.
3. Модуль зубчатого зацепления m. Показывает, какое количество миллиметров диаметра делительной окружности приходится на один зуб зацепления. Является основной геометрической характеристикой, через которую определяются другие основные параметры зубчатых колес и зуборезного инструмента. В косозубых передачах различают нормальный модуль mn, определяемый в плоскости, перпендикулярной линии зубьев (нормальной плоскости), и окружной (делительный) mt, определяемый в торцевой плоскости зубчатого колеса. Окружной модуль mt пропорционален окружному шагу Pt и равен mt = 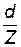 , где d – диаметр делительной окружности, а Z – число зубьев.
, где d – диаметр делительной окружности, а Z – число зубьев.
Нормальный модуль mn= mt × cos β – определяется с учетом угла наклона зубьев β.
Для прямозубых передач нормальные и окружные шаги, а также нормальные и окружные модули совпадают.
4. Окружности диаметрами d1 и d2 называются начальными (с них начинается построение) или делительными (они делят зуб на головку ha и ножку hƒ). Делительные диаметры у шестерни (d1) и колеса (d2) определяются зависимостями:
d1 = mt × Z1, d2 = mt × Z2. (1)
5. Окружности диаметрами da1 и da2, ограничивающие зубья по высоте, называются окружностями выступов. Их диаметры определяются зависимостями:
da1= d1 + 2mn, da2 = d2 + 2mn. (2)
6. Окружности диаметрами dƒ1 и dƒ2, ограничивающие зубья по глубине, называются окружностями впадин. Их диаметры определяются зависимостями:
dƒ1 = d1 – 2,5mn, dƒ2 = d2 – 2,5mn. (3)
7. Высота зуба h равна сумме высот головки ha и ножки hƒ зуба:
ha = mn; hƒ = 1,25mn; h = ha + hƒ = 2,25mn.
8. Радиальный зазор C – расстояние между впадинами зубьев шестерни и головками зубьев колеса,
C = 0,25mn.
9. Межосевое расстояниеаω – расстояние между центрами (осями) вращения шестерни и колеса:
аω = 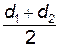 = 0,5(Z1 + Z2) mt.
= 0,5(Z1 + Z2) mt.
10. Угол зацепленияα – угол между линией зацепления, проходящий через полюс П и касательной к обеим делительным окружностям. В некорригированном зацеплении обычно α = 20о.
Методика определения основных параметров
зубчатых зацеплений редуктора
При выполнении работы необходимо определить основные геометрические параметры зубчатых зацеплений быстроходной (ступень 1) и тихоходной (ступень 2) косозубых передач двухступенчатого цилиндрического редуктора, а также рассчитать его некоторые кинематические параметры. Основные геометрические и некоторые кинематические параметры показаны на кинематической схеме редуктора (рис. 6). После измерений и вычислений параметров их значения необходимо указать в соответствующих графах итоговой таблицы (по образцу табл. 9 в графах «Измеренные», «Рассчитанные», «Стандартные»), а некоторые указать на кинематической схеме редуктора.
Значения основных параметров зацеплений либо определяются замерами штангенциркулем, линейкой, кронциркулем, либо вычисляются по зависимостям (1)–(3), после чего для полученных значений модуля выбирается его ближайшее стандартное значение из стандартного ряда и по этому значению выполняются дальнейшие вычисления других геометрических параметров.
Шаг зубчатого зацепления P определяется отдельно для быстроходной (индекс «1») и тихоходной (индекс «2») ступеней. Поскольку каждое зацепление косозубое, то измеряются два шага – окружной Pt1 (Pt2)
и нормальный Pn1 (Pn2). При контроле за точностью изготовления зубчатых колес используется специальный измерительный прибор – шагомер, позволяющий установить шаг по длине дуги делительной окружности. В учебных лабораториях такого прибора часто не бывает. Поэтому для ориентировочного определения шага зацепления по хорде окружности выступов можно пользоваться ниже следующим способом. Приблизительно с небольшой долей погрешности (~4 %) можно определить величину и нормального Pn, и тангенциального Pt шагов, измерив расстояние между одноименными точками вершин зубьев (хорды окружностей выступов) в соответствующих плоскостях. Другой практический способ измерения шагов (также с небольшой погрешностью) приведен ниже при определении углов наклона зубьев.
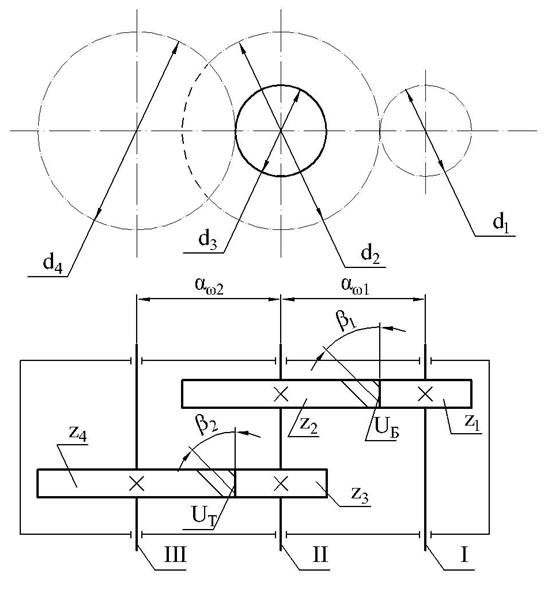
Рис. 6. Кинематическая схема двухступенчатого редуктора:
I – ведущий (входной) вал; II – промежуточный вал; III – ведомый (выходной) вал; UБ – частное передаточное число быстроходной ступени;
UТ – частное передаточное число тихоходной ступени
Угол наклона зубьевβ1 (β2) определяется для быстроходной и тихоходной ступеней редуктора следующим образом. Расположив край тетрадного листа вдоль торцевой плоскости t-t (рис. 7), проводят с усилием по листу пальцем (или ногтем) вдоль 3...4 вершин зубьев колеса быстроходной и колеса тихоходной ступеней редуктора, получая на обратной стороне листа 3...4 параллельных следа (отпечатка) вершин зубьев. Затем листы снимают, переворачивают и продлевают карандашом один отпечаток до пересечения в т.В с вертикальным катетом у1 (у2), который проводят из т.А. Горизонтальный катет х1 (х2) проводят из т.О – вершины угла β1 (β2) – на длину 100 мм (до т. А). Линейкой измеряют полученную длину катета у1 (у2) в мм и вычисляют тангенс угла по зависимости
tg β1(β2) = 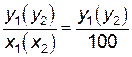 =
=

Рис. 7. Схема для определения углов наклона зубьев β1 (β2),
окружных Pt1 (Pt2) и нормальных Pn1 (Pn2) шагов в зацеплениях быстроходной (1) и тихоходной (2) косозубых передач
По табл. 4 находят значение углов наклона зубьев β1 (β2), промежуточные значения минут находят методом экстраполяции.
Таблица 4
Значения углов наклона зубьев β1 (β2)
при различных значениях tg β1 (β2)
| Угол наклона зубьев β1 (β2) | минуты градусы | 0¢ | 20¢ | 40¢ |
| 0,1228 | 0,1287 | 0,1346 | ||
| 0,1405 | 0,1465 | 0,1524 | ||
| 0,1584 | 0,1644 | 0,1703 | ||
| 0,1763 | 0,1823 | 0,1883 | ||
| 0,1944 | 0,2004 | 0,2065 | ||
| 0,2126 | 0,2186 | 0,2247 |
По образцу (см. рис. 7) на листе бумаге с помощью штангенциркуля определяют в показанных направлениях величины нормальных Pn1 (Pn2) и окружных Pt1 (Pt2) шагов с точностью до 0,5 мм и сравнивают значения шагов, полученные на листах бумаги, со значениями шагов, измеренных натурально между одноименными точками вершин зубьев.
Для дальнейших вычислений принимают средние значения шагов 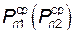 и
и 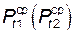 . Полученные значения шагов заносят в итоговую табл. 9 в графу «Измеренные».
. Полученные значения шагов заносят в итоговую табл. 9 в графу «Измеренные».
Числа зубьев шестерен и колес Z1, Z2 и Z3, Z4 для быстроходной и тихоходной ступеней редуктора определяются подсчетом в соответствии с рис. 6. Во избежание ошибок при подсчетах числа зубьев рекомендуется отмеченный мелом зуб считать последним.
Подсчитанные числа зубьев следует занести в итоговую табл. 9 в графу «Измеренные».
Модули зубчатых зацеплений.Модуль является основной геометрической характеристикой зубчатого зацепления и в лабораторной работе определяется для обеих передач редуктора.
В косозубой передаче различают два модуля: нормальный mn – в плоскости, перпендикулярной линии зубьев, и окружной mt – в торцевой плоскости.
В прямозубой передаче существует только нормальный модуль m (без индекса). Значения модулей в мм можно определить расчетным путем по следующим зависимостям:
Ø для быстроходной ступени редуктора
нормальный модуль 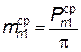 ,
,
окружной модуль 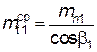 ;
;
Ø для тихоходной ступени редуктора
нормальный модуль 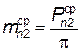 ,
,
окружной модуль 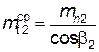 ,
,
где 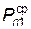 и и 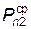 – –
| усредненные нормальные шаги в зацеплении быстроходной и тихоходной ступеней; |
| β1 и β2 – | углы наклона зубьев быстроходной и тихоходной ступеней. |
Значения cos β1 и cos β2 принимают из табл. 5.
Таблица 5
Значения cos β при различных углах наклона зубьев β
| Угол наклона зубьев β | минуты градусы | 0¢ | 20¢ | 40¢ |
| 0,9925 | 0,9918 | 0,9911 | ||
| 0,9903 | 0,9894 | 0,9886 | ||
| 0,9877 | 0,9868 | 0,9858 | ||
| 0,9848 | 0,9838 | 0,9827 | ||
| 0,9816 | 0,9805 | 0,9793 | ||
| 0,9781 | 0,9769 | 0,9757 | ||
| 0,9744 | 0,9730 | 0,9717 |
Промежуточные значения cos β находят методом экстраполяции.
Полученные расчетные значения нормальных и окружных модулей следует занести в итоговую таблицу в графу «Рассчитанные». Затем надо определить нормальные модули быстроходной Pn1 и тихоходной Pn2 ступеней через измеренные высоты зубьев h1 и h2 – соответственно. Полные высоты h1 и h2 измеряются штангенциркулем с глубиномером
с точностью до 0,1 мм, величины измеренных модулей в мм определяются зависимостями:
Ø для быстроходной ступени 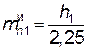 ;
;
Ø для тихоходной ступени 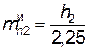 .
.
Полученные значения модулей занести в итоговую таблицу
(см. табл. 9), в графу «Измеренные».
Затем по табл. 6 принять ближайшие к полученным усредненным расчетным значениям нормальных модулей 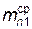 и
и 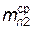 и измеренным значениям нормальных модулей
и измеренным значениям нормальных модулей 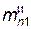 и
и 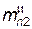 стандартные значения нормальных модулей mn1 и mn2. Принятые для обеих передач стандартные значения нормальных модулей mn1 и mn2 в мм занести в итоговую таблицу в графу «Стандартные».
стандартные значения нормальных модулей mn1 и mn2. Принятые для обеих передач стандартные значения нормальных модулей mn1 и mn2 в мм занести в итоговую таблицу в графу «Стандартные».
Таблица 6
Стандартные значения нормальных модулей
| Ряд | Значения нормального модуля mn, мм |
| 1-й | 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12 |
| 2-й | 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11 |
1-й ряд является предпочтительным.
Высоты зубьев шестерни и колеса одной ступени всегда одинаковые. Поэтому измерять приблизительные высоты зубьев удобнее и точнее на колесах каждой ступени. Полная высота зуба h есть сумма высот головки ha и ножки hƒ (см. рис. 4), т.е. h = ha + hƒ. С помощью штангенциркуля с глубиномером измерить приблизительную полную высоту зубьев быстроходной h1 и тихоходной h2 ступеней в мм с точностью до 0,1 мм. Затем определить высоты головок ha и ножек hƒ зубьев в мм с точностью до 0,1 мм по зависимостям:
· для быстроходной ступени:
ha1 = mn1; hƒ = 1,25 mn1 с проверкой h1 = ha1 + hƒ1 = 2,25mn1;
· для тихоходной ступени:
ha2 = mn2 ; hƒ = 1,25 mn2 с проверкой h2 = ha2 + hƒ2 = 2,25mn2,
| где mn1 и mn2 – | нормальные стандартные модули. |
Сравнить результаты измерений и вычислений и занести их в итоговую таблицу в графы «Измеренные» и «Рассчитанные» соответственно.
Диаметры окружностей
При построении некорригированного эвольвентного зубчатого зацепления для шестерни и для колеса одной ступени определяют размеры трех концентрических окружностей, проведенных из центров вращения шестерни О1 и колеса О2: делительной (начальной) окружности, окружности вступов и окружности впадин (см. рис.5). Основной размер окружностей – их диаметры.
Диаметры делительных окружностей d1, d2, d3, d4 (см. рис.5) рассчитываются в мм с точностью до 0,1 мм после определения нормальных (mn1 и mn2) и расчетных окружных (mt1 и mt2) модулей, а также подсчета числа зубьев шестерен (Z1 и Z3) и колес (Z2 и Z4) обеих ступеней по следующим зависимостям:
· быстроходная ступень:
для шестерни 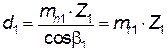 ,
,
для колеса 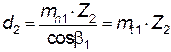 ;
;
· тихоходная ступень:
для шестерни 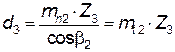 ,
,
для колеса 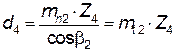 .
.
Полученные результаты указываются на рис.5 и заносят в итоговую таблицу в графу «Рассчитанные».
Диаметры окружностей выступов da1, da2, da3, da4 (см. рис. 5) измеряют в мм для шестерен и колес на разобранном редукторе с помощью штангенциркуля и кронциркуля с точностью до 0,1 мм и заносят в итоговую таблицу в графу «Измеренные».
Затем эти диаметры рассчитывают по зависимостям:
· быстроходная ступень:
для шестерни da1 = d1 + 2mn1,
для колеса da2 = d2 + 2mn1;
· тихоходная ступень:
для шестерни da3 = d3 + 2mn2,
для колеса da4 = d4 + 2mn2.
Полученные результаты указывают на рис. 5 и заносят в итоговую таблицу в графу «Рассчитанные».
Диаметры окружностей впадин dƒ1, dƒ2, dƒ3, dƒ4 (см. рис. 5) измеряют в мм для шестерен и колес на разобранном редукторе с помощью штангенциркуля и кронциркуля с точностью до 0,1 мм и заносят в итоговую таблицу в графу «Измеренные».
Затем эти диаметры рассчитывают по зависимостям:
· быстроходная ступень:
для шестерни dƒ1 = d1 – 2,5mn1,
для колеса dƒ2 = d2 – 2,5mn1;
· тихоходная ступень:
для шестерни dƒ3 = d3 – 2,5mn2,
для колеса dƒ4 = d4 – 2,5mn2.
Полученные результаты указывают на рис. 5, заносят в итоговую таблицу в графу «Рассчитанные».
Межосевые расстояния аω1, аω2 (см. рис. 6) определяют замерами на собранном редукторе между осями вращения валов быстроходной aω1 и тихоходной aω2 ступеней штангенциркулем с точностью до 0,1 мм. Результаты заносят в итоговую таблицу в графу «Измеренные».
Затем эти расстояния рассчитывают для быстроходной и тихоходной ступеней по зависимостям:
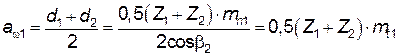 ;
;
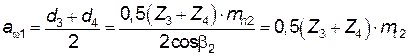 .
.
Полученные результаты заносят в итоговую таблицу в графу «Рассчитанные». После замеров и вычислений из табл. 7 принимают ближайшие стандартные значения aω1 и aω2 и заносят их в итоговую таблицу в графу «Стандартные».
Таблица 7
Стандартные значения межосевых расстояний
цилиндрических передач редукторов, мм
| Ряд | Значения межосевых расстояний aω, мм |
| 1-й | 40; 50; 63; 80; 100; 125; 160; 200; 250 |
| 2-й | 140; 180; 125; 280; 355 |
Передаточные числа быстроходной (UБ) и тихоходной (UТ) ступеней редуктора (частные передаточные числа) определяются расчетным путем в соответствии с рис. 6 по следующим соотношениям:
UБ = 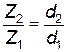 ; UТ =
; UТ = 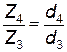 ,
,
| где Z1, Z2, Z3, Z4 – | числа зубьев шестерен и колес быстроходной и тихоходной ступеней (см. рис. 6); |
| d1, d2, d3, d4 – | диаметры делительных окружностей шестерен и колес быстроходной и тихоходной ступеней (см. рис. 6). |
Полученные значения заносят в итоговую таблицу в графу «Рассчитанные».
По табл. 8 выбирают ближайшие номинальные значения передаточных чисел UБ и UТ по ГОСТ 2185–66 и заносят их в итоговую таблицу в графу «Стандартные».
Таблица 8
Номинальные передаточные числа зубчатых передач редукторов (ГОСТ 2185–66)
| Ряд | Значения номинальных передаточных чисел |
| 1-й | 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10 |
| 2-й | 1,12; 1,4; 1,8; 2,24; 2,8; 3,55; 4,5; 5,6; 7,1; 9,0 |
Таблица 9
Итоговая таблица результатов
| № п/п | Параметры размерность | Обозначение | Результаты | ||
| Измер. | Рассчит. | Стандарт. | |||
| Шаг зацепления, мм: | |||||
| – нормальной быстроходной ступени | Pn1 | ||||
| – окружной быстроходной ступени | Pt1 | ||||
| – нормальной тихоходной ступени | Pn2 | ||||
| – окружной тихоходной ступени | Pt2 | ||||
| Угол наклона зубьев, град, мин: | |||||
| –быстроходной ступени | β1 | ||||
| – тихоходной ступени | β2 |
Продолжение табл.9
| Число зубьев, шт.: | |||||
| – шестерни быстроходной ступени | Z1 | ||||
| – колеса быстроходной ступени | Z2 | ||||
| – шестерни тихоходной ступени | Z3 | ||||
| – колеса тихоходной ступени | Z4 | ||||
| Модуль зубчатого зацепления, мм: | |||||
| – нормальной быстроходной ступени | mn1 | ||||
| – окружной быстроходной ступени | mt1 | ||||
| – нормальной тихоходной ступени | mn2 | ||||
| – окружной тихоходной ступени | mt2 | ||||
| Высота зубьев, мм: | |||||
| – полная быстроходной ступени | h1 | ||||
| – головки быстроходной ступени | ha1 | ||||
| – ножки быстроходной ступени | hƒ1 | ||||
| – полная тихоходной ступени | h2 | ||||
| – головки тихоходной ступени | ha2 | ||||
| – ножки тихоходной ступени | hƒ2 | ||||
| Диаметр окружной, мм, | |||||
| делительной быстроходной ступени: | |||||
| – шестерни | d1 | ||||
| – колеса | d2 | ||||
| делительной тихоходной ступени: | |||||
| – шестерни | d3 | ||||
| – колеса | d4 | ||||
| выступов быстроходной ступени: | |||||
| – шестерни | da1 | ||||
| – колеса | da2 | ||||
| выступов тихоходной ступени: | |||||
| – шестерни | da3 | ||||
| – колеса | da4 | ||||
| впадин быстроходной ступени: | |||||
| – шестерни | dƒ1 | ||||
| – колеса | dƒ2 | ||||
| впадин тихоходной ступени: | |||||
| – шестерни | dƒ3 | ||||
| – колеса | dƒ4 |
Окончание табл.9
| Межосевое расстояние, мм: | |||||
| – быстроходной ступени | aω1 | ||||
| – тихоходной ступени | aω2 | ||||
| Передаточное число: | |||||
| – быстроходной ступени | UБ | ||||
| – тихоходной ступени | UТ |
Содержание отчета
Отчет должен быть оформлен в соответствии с общими требования к отчетам по лабораторным работам. Кроме того, в отчете должны быть:
1. Схема эвольвентного зацепления быстроходной и тихоходной ступеней редуктора, выполненная в масштабе 1:1 или 2:1, с указанием основных параметров зацепления и их значений по образцу, приведенному на рис. 5.
2. Кинематическая схема двухступенчатого редуктора с указанием основных параметров и их значений по образцу, представленному на рис. 6.
3. Расчетная часть с определением расчетных параметров и их значений.
4. Итоговая таблица результатов, оформленная по образцу итоговой табл. 9.
Контрольные вопросы
1. Какие параметры зубчатого зацепления определялись в лабораторной работе?
2. Что такое модуль зацепления, как и для чего он определяется и что показывает?
3. Как определяются нормальные и окружные шаги и модули косозубого эвольвентного зацепления?
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ
ЧЕРВЯЧНОЙ ПЕРЕДАЧИ РЕДУКТОРА
Цель работы– научиться определять экспериментальным и расчетным путем основные геометрические и кинематические параметры червячных передач, являющихся основой конструкции червячных цилиндрических редукторов.
Содержание работы
1. Ознакомиться с принципом действия и конструктивными особенностями червячных передач и редукторов на их основе.
2. Изобразить схему червячной цилиндрической передачи с указанием на ней полученных при выполнении лабораторной работы значений основных параметров (по образцу, приведенному на рис. 11).
3. Определить замерами и расчетами основные параметры червячной передачи.
4. Результаты измерений и расчетов занести в итоговую таблицу (по образцу табл. 10).
5. Оформить отчет и ответить (устно) на контрольные вопросы.
Лабораторное оборудование и инструменты:
1. Червячные редукторы различных типоразмеров – 2 шт. (один редуктор на бригаду, по указанию преподавателя).
2. Штангенциркуль с нутро- и глубиномером (типа «колумбус») – 2 шт.
3. Линейка длиной 300 мм – 2 шт.
4. Кронциркуль – 2 шт.
Дата: 2016-10-02, просмотров: 329.