◦Область определения: .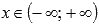

◦Область значений: .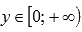

◦Функция четная, так как .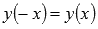

◦Функция возрастает при 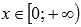, убывает при .

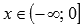◦Функция выпуклая при .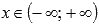

◦Точек перегиба нет.

◦Асимптот нет.

◦Функция проходит через точки (-1;1) , (0;0) , (1;1) .

VIII.Пусть 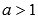и и а – несократимая рациональная дробь с четным знаменателем (например, а=7/4 или 11/8 )

В этом случае график степенной функции будет иметь вид: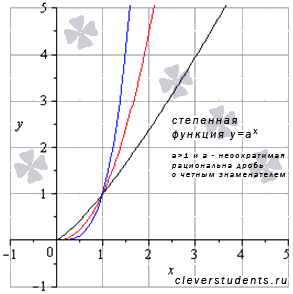

В качестве примера взяты а=5/4 – черная линия, а=13/6 – красная линия, а=7/2 – синяя линия.

Свойства степенной функции с положительным рациональным показателем большим единицы.

◦Область определения: .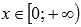

◦Область значений: .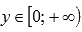

◦Функция не является ни четной, ни нечетной, то есть она общего вида.

◦Функция возрастает при .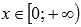

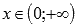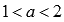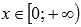◦Функция вогнутая при , если ; при , если .

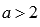◦Точек перегиба нет.

◦Асимптот нет.

◦Функция проходит через точки (0;0) , (1;1) .

Замечание.

Если 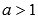и а – иррациональное число (например, корень четвертой степени из 19,23 ), то вид графика степенной функции с иррациональным показателем аналогичен рассмотренным в этом пункте, свойства абсолютно схожи.

IX.Пусть 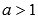и если числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, а сама дробь несократима (например, 7/3 или 25/7), то областью определения такой функции принято считать все действительные числа 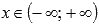, и область значений будет .

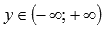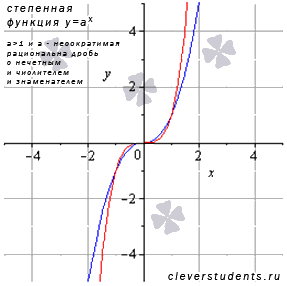График степенной функции с рациональным показателем в этом случае будет иметь вид, схожий с:

В качестве примера взяты а=7/3 – синяя линия, а=25/7 – красная линия.

Свойства степенной функции с положительным рациональным показателем большим единицы.

◦Область определения: .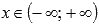

◦Область значений: .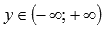

◦Функция нечетная, так как .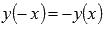

◦Функция возрастает при .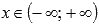

◦Функция вогнутая при 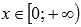и выпуклая при .

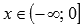◦Точка (0;0) является точкой перегиба.

◦Асимптот нет.

◦Функция проходит через точки (-1;-1) , (0;0) , (1;1) .

X.Пусть 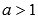и если числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число и сама дробь несократима (например, 8/3 или 16/7 ), то областью определения такой функции принято считать все действительные числа 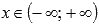,и область значений будет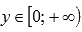

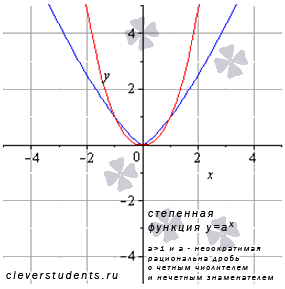График степенной функции в этом случае будет иметь вид, схожий с:

В качестве примера взяты а=4/3 – синяя линия, а=16/7 – красная линия.

Свойства степенной функции с положительным рациональным показателем большим единицы.

◦Область определения: .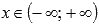

◦Область значений: .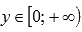

◦Функция четная, так как .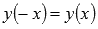

◦Функция возрастает при 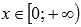, убывает при .

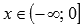◦Функция вогнутая при .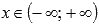

◦Точек перегиба нет.

◦Асимптот нет. Функция проходит через точки (-1;1) , (0;0) , (1;1) .

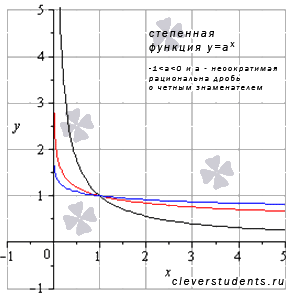XI.Пусть 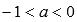и а – несократимая рациональная дробь с четным знаменателем (например, а=-1/2 или -5/8 ).

В этом случае график степенной функции будет иметь вид:

В качестве примера взяты а=-1/4 – красная линия, а=-1/8 – синяя линия, а=-5/6 – черная линия.

Свойства степенной функции с отрицательным рациональным показателем.

◦Область определения: .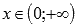

Поведение на границе области определения 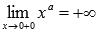при 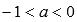и а – рациональная дробь. Следовательно, х=0 является вертикальной асимптотой.

◦Область значений: .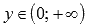

◦Функция не является ни четной, ни нечетной, то есть она общего вида.

◦Функция убывает при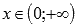

◦Функция вогнутая при .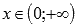

◦Точек перегиба нет.

◦Горизонтальной асимптотой является прямая y=0 .

◦Функция проходит через точку (1;1) .

Замечание.

Если 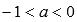и а – иррациональное число (например, минус корень четвертой степени из 0,21 ), то вид графика степенной функции с отрицательным иррациональным показателем аналогичен рассмотренным в этом пункте, свойства абсолютно схожи.

XII.Пусть 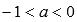и если числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, а сама дробь несократима (к примеру, -1/3 или -5/7), тогда областью определения такой функции принято считать , и область значений будет .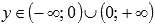

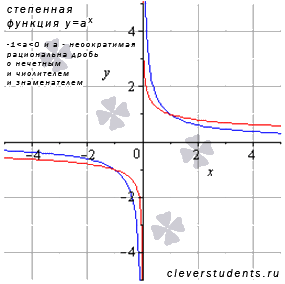График функции в этом случае будет иметь вид, схожий с:

В качестве примера взяты а=-5/7 – синяя линия, а=-1/3 – красная линия.