Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Свойства степенной функции с четным положительным показателем.

◦Область определения: x ? (-∞;+∞)

◦Область значений: y ? [0;+∞)

◦Функция четная, так как y(-x)=y(x).

◦Функция возрастает при x ? [0;+∞)., убывает при x ? (-∞;0]

◦Функция вогнутая при x ? (-∞;+∞).

◦Точек перегиба нет.

◦Асимптот нет.

◦Функция проходит через точки (-1;1) , (0;0) , (1;1) .

III.Пусть а=-1, -3, -5, …

В этом случае график степенной функции будет иметь вид: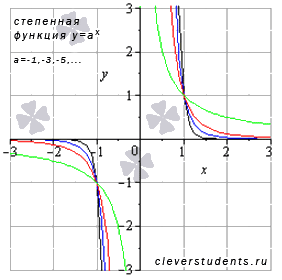

В качестве примера взяты а=-9 – черная линия, а=-5 – синяя линия, а=-3 – красная линия, а=-1 – зеленая линия. При а=-1 имеем обратную пропорциональность ( гиперболу ) - частный случай степенной.

Свойства степенной функции с нечетным отрицательным показателем.

◦Область определения: x ? (-∞;0) U x ? (0;+∞). При x=0 имеем разрыв второго рода, так как

Lim(x→0-0) x^a = -∞, lim (x→0+0) x^a = +∞,при а=-1, -3, -5, …. Следовательно, прямая x=0 является вертикальной асимптотой.

◦Область значений: y ? (-∞;0) U ? (0;+∞).

◦Функция нечетная, так как y(-x)=-y(x).

◦Функция убывает при x ? (-∞;0)U (0;+∞).

◦Функция выпуклая при x ? (-∞;0) и вогнутая при x ? (0;+∞).

◦Точек перегиба нет.

 

◦Горизонтальной асимптотой является прямая y=0 , так как

k= lim(x→∞) x^a/x =0, b= lim(x→∞) x^a-kx = 0

y=kx+b = 0 при а=-1, -3, -5, … .

◦Функция проходит через точки (-1;-1) , (1;1) .

IV.Пусть а=-2, -4, -6, …

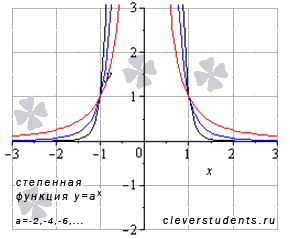В этом случае график степенной функции будет иметь вид:

В качестве примера взяты а=-8 – черная линия, а=-4 – синяя линия, а=-2 – красная линия.

Свойства степенной функции с четным отрицательным показателем.

◦Область определения: x ? (-∞;0)U (0;+∞).

При x=0 имеем разрыв второго рода, так как

Lim(x→0-0) x^a = +∞, Lim(x→0+0) x^a = +∞ при а=-2, -4, -6, … . Следовательно, прямая x=0 является вертикальной асимптотой.

◦Область значений: y ? (0;+∞) .

◦Функция четная, так как y(-x)=y(x).

◦Функция возрастает при x ? (-∞;0), убывает при x? (0;+∞)

◦Функция вогнутая при x ? (-∞;0)U(0;+∞).

◦Точек перегиба нет.

◦Горизонтальной асимптотой является прямая y=0 , так как

Lim(x→∞) x^a /x= 0, Lim(x→0+0) (x^a-kx) = 0

y=kx+b+0 при а=-2, -4, -6, … .

◦Функция проходит через точки (-1;1) , (1;1) .

V.Пусть 0<a<1 и а – несократимая рациональная дробь с четным знаменателем (например, а=1/4 или 3/8 ).

 

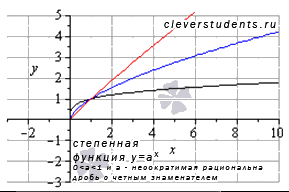
В этом случае график степенной функции будет иметь вид:

В качестве примера взяты а=1/4 – черная линия, а=5/8 – синяя линия, а=11/12 – красная линия.

Свойства степенной функции с положительным рациональным показателем меньшим единицы.

◦Область определения:x?[0;+∞) .

◦Область значений: y?[0;+∞).

◦Функция не является ни четной, ни нечетной, то есть она общего вида.

◦Функция возрастает при x?[0;+∞) .

◦Функция выпуклая при x?[0;+∞).

◦Точек перегиба нет.

◦Асимптот нет.

◦Функция проходит через точки (0;0) , (1;1) .

Замечание.

Если 0<a<1 и а – иррациональное число, то вид графика степенной функции аналогичен рассмотренным в этом пункте, свойства степенной функции с иррациональным показателем абсолютно схожи.

Замечание о важности несократимости рациональной дроби в показателе степени.

графики функций y=x^2/₆ и y=x^1/₃ не есть одно и то же, если не оговорен момент о несократимости показателя степени. Этим мы НЕ ХОТИМ сказать, что 2/6=/ 1/3, но y=x^2/₆ можно трактовать по-разному, y= x^2/₆ = (6корней х)² или y= x2/6 = (6корней х²) . Удивительно, ни первая, ни вторая функция не соответствуют y=x^1/₃.

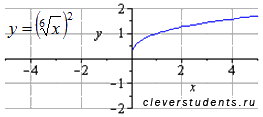Вот тому графическая иллюстрация:

 

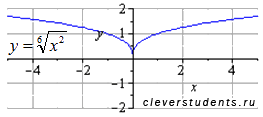
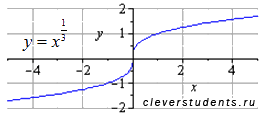
В дальнейшем y=x^m_/n будем рассматривать как y= (n корней из x^m)

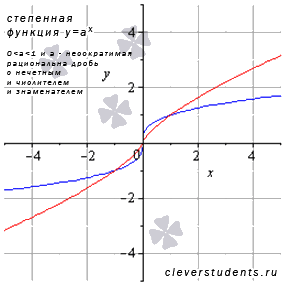VI.Пусть 0<a<1 и если числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, а сама дробь несократима (например, 1/3 или 5/7), то областью определения такой функции принято считать все действительные числа 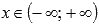, и область значений будет .

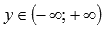График степенной функции в этом случае будет иметь вид, схожий с:

В качестве примера взяты а=1/3 – синяя линия, а=5/7 – красная линия.

Свойства степенной функции с положительным рациональным показателем большим единицы.

◦Область определения: .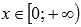

◦Область значений: .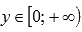

◦Функция не является ни четной, ни нечетной, то есть она общего вида.

◦Функция возрастает при .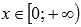

◦Функция вогнутая при 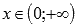, есл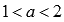и ; при 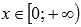, если .

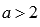◦Точек перегиба нет.

◦Асимптот нет.

◦Функция проходит через точки (0;0) , (1;1) .

Замечание.

Если 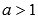и а – иррациональное число (например, корень четвертой степени из 19,23 ), то вид графика степенной функции с иррациональным показателем аналогичен рассмотренным в этом пункте, свойства абсолютно схожи.

IX.Пусть 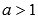и если числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, а сама дробь несократима (например, 7/3 или 25/7), то областью определения такой функции принято считать все действительные числа 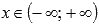, и область значений будет .

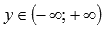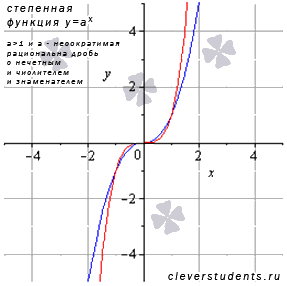График степенной функции с рациональным показателем в этом случае будет иметь вид, схожий с:

В качестве примера взяты а=7/3 – синяя линия, а=25/7 – красная линия.

Замечание.

Если 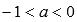и а – иррациональное число (например, минус корень четвертой степени из 0,21 ), то вид графика степенной функции с отрицательным иррациональным показателем аналогичен рассмотренным в этом пункте, свойства абсолютно схожи.

 

XII.Пусть 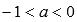и если числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, а сама дробь несократима (к примеру, -1/3 или -5/7), тогда областью определения такой функции принято считать , и область значений будет .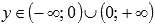

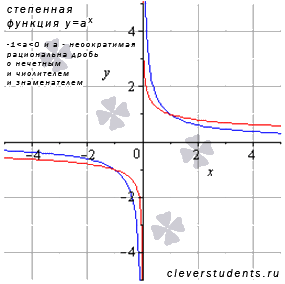График функции в этом случае будет иметь вид, схожий с:

В качестве примера взяты а=-5/7 – синяя линия, а=-1/3 – красная линия.

Замечание.

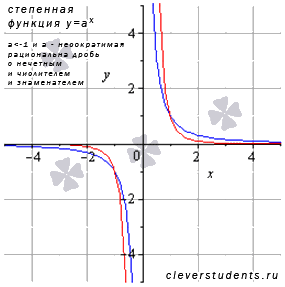Если 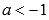и а – иррациональное число (например, минус корень квадратный из семи), то вид графика аналогичен рассмотренным в этом пункте, свойства абсолютно схожи.

XV.Пусть 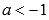и если числитель и знаменатель рациональной дроби в показателе степени представляет собой нечетные числа, а сама дробь несократима (к примеру, -5/3 или -25/7), тогда областью определения такой функции принято считать , и область значений будет .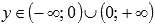

График степенной функции с рациональным показателем в этом случае будет иметь вид, схожий с:

В качестве примера взяты а=-5/3 – синяя линия, а=-17/5 – красная линия.

 

Логарифмические ,

I.При 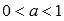логарифмическая функция будет иметь следующий вид:

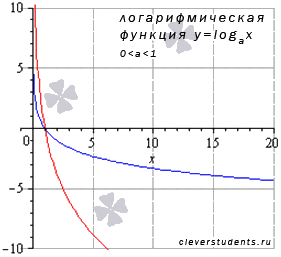Для примера представлены графики функции логарифма при а=1/2 – синяя линия, a=5/6 – красная линия.

Тригонометрические

◦Функция синус y=sin(x)

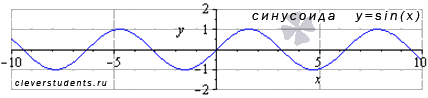
Свойства функции y=sinx.

◦Область определения: .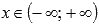

◦Наименьший положительный период .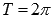

◦Функция обращается в ноль при 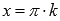, где 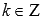, Z – множество целых чисел.

◦Область значений: .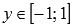

◦Функция синус - нечетная, так как .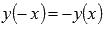

◦Функция убывает при ,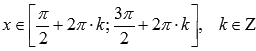

возрастает при .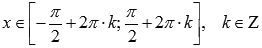

◦Функция имеет локальные максимумы в точках ,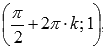

локальные минимумы в точках .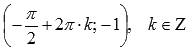

◦Функция вогнутая при ,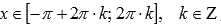

выпуклая при .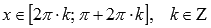

◦Координаты точек перегиба .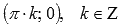

◦Асимптот нет.

◦Функция косинус y=cos(x)

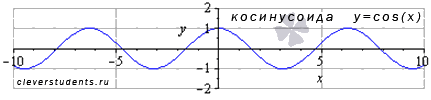
Свойства функции y=cosx.

◦Область определения: .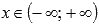

◦Наименьший положительный период косинусоиды .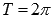

◦Функция обращается в ноль при 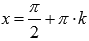, где 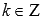, Z – множество целых чисел.

◦Область значений: .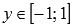

◦Функция косинус - четная, так как .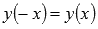

◦Функция убывает при 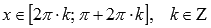возрастает при .

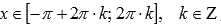◦Функция имеет локальные максимумы в точках ,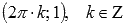

локальные минимумы в точках .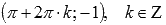

◦Функция вогнутая при ,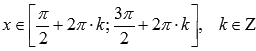

выпуклая при .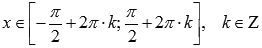

◦Координаты точек перегиба .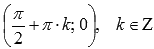

◦Асимптот нет.

◦Функция тангенс y=tg(x)

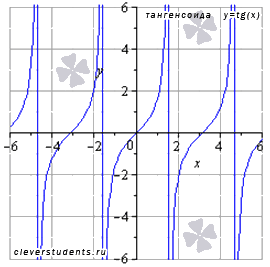
Свойства функции y=tgx.

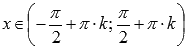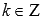◦Область определения : , где , Z – множество целых чисел.

Поведение на границе области определения

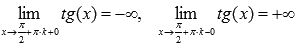
Следовательно, прямы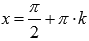е , где 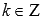, являются вертикальными асимптотами.

◦Наименьший положительный период тангенсоиды .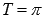

◦Функция обращается в ноль при 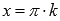, где 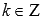, Z – множество целых чисел.

◦Область значений: .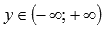

◦Функция тангенс - нечетная, так как .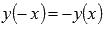

◦Функция возрастает при .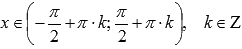

◦Функция вогнутая при ,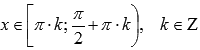

выпуклая при .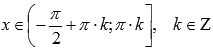

◦Координаты точек перегиба .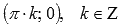

◦Наклонных и горизонтальных асимптот нет.

 

◦Функция котангенс y=ctg(x)

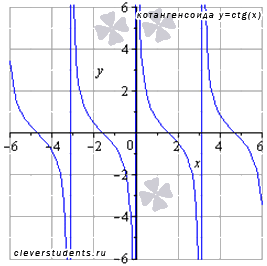
Свойства функции y=ctgx.

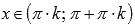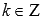◦Область определения: , где , Z – множество целых чисел.

 

 

Поведение на границе области определения

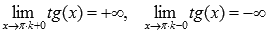
Следовательно, прямы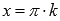е , где 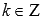являются вертикальными асимптотами.

◦Наименьший положительный период .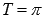

◦Функция обращается в ноль при 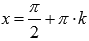, где 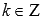, Z – множество целых чисел.

◦Область значений функции котангенс: .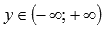

◦Функция нечетная, так как .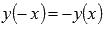

◦Функция убывает при .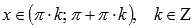

◦Функция котангенс вогнутая при ,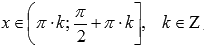

выпуклая при .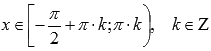

◦Координаты точек перегиба .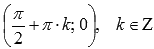

◦Наклонных и горизонтальных асимптот нет.

 

Решение.

Функция представляется в следующем виде:

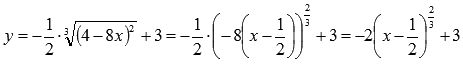
Имеем k1=2, причем перед этим коэффициентом знак «минус»,

а=-1/2 , b=3 . Следовательно, получили цепочку геометрических преобразований графика: растяжение вдоль оси ординат вдвое, симметричное отображение относительно оси абсцисс, сдвиг вправо на 1/2 и сдвиг вверх на 3 единицы.

исходная степенная функция

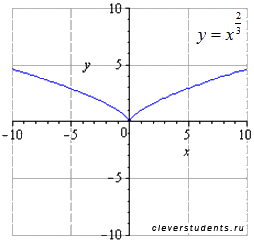
растягиваем вдоль оси oy вдвое

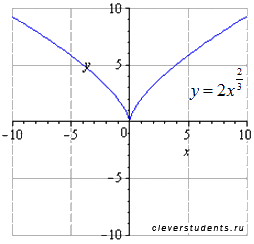
отображаем симметрично относительно оси ox

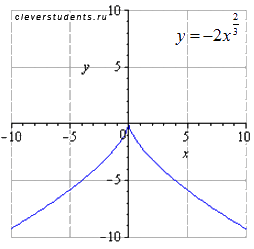
сдвигаем вправо на 1/2

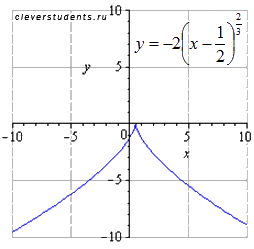
сдвигаем вверх на 3 единицы

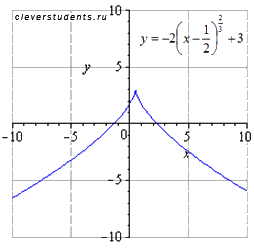
Пример (преобразование графика показательной функции).

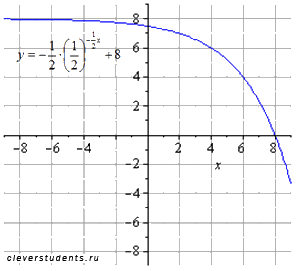
Построить график показательной функции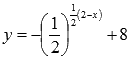

Решение.

По свойствам степени преобразуем функцию:

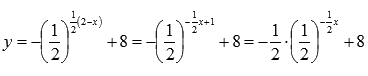
Таким образом, имеем цепочку преобразований графика показательной функции :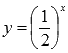

 

 

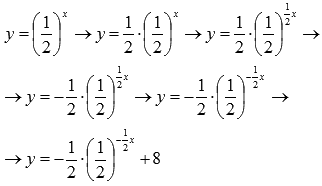
исходная показательная функция

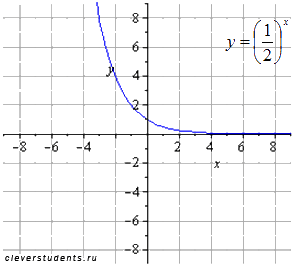
сжимаем вдоль оси oy вдвое

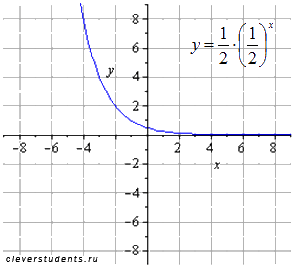
растягиваем вдвое вдоль оси ox

 

 

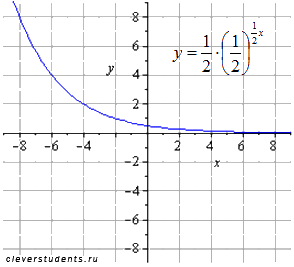
отображаем симметрично относительно оси ox

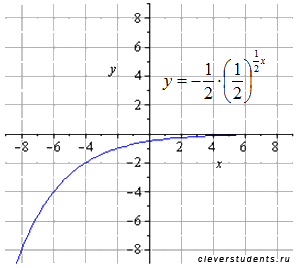
отображаем симметрично относительно оси oy

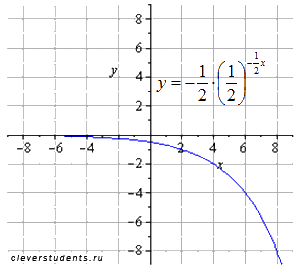
сдвигаем вверх на 8 единиц

 

Пример (геометрические преобразования графика логарифмической функции y=ln(x)).

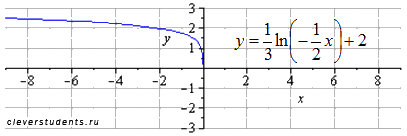
Построить 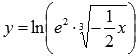преобразованием графика функции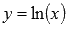

Решение.

Используем свойства логарифма:

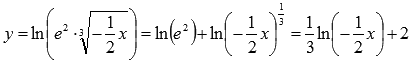
Таким образом, имеем цепочку преобразований графика логарифмической функции:

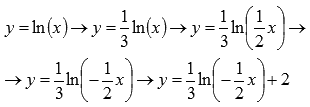
график исходной функции натуральный логарифм

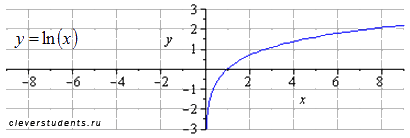
сжимаем вдоль оси oy втрое

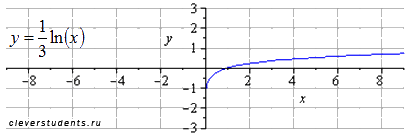
растягиваем вдвое вдоль оси ox

отображаем симметрично относительно оси oy

сдвигаем вверх на 2 единицы

Преобразование графиков тригонометрических функций подчиняется общей схеме геометрических преобразований 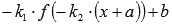. Единственно хочется обратить внимание на влияние коэффициента k2 на период тригонометрических функций. При отличном от единицы коэффициенте k2 период становится равным 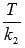. То есть, при 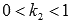растяжение графика функции вдоль оси абсцисс соответствует увеличению периода, а при 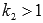сжатие графика соответствует уменьшению периода. Коэффициент k1 влияет на амплитуду колебаний синусоиды и косинусоиды.

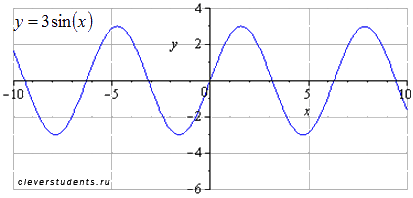
Пример (геометрические преобразования синусоиды y=sinx).

С помощью преобразования графика функции y=sinx построить

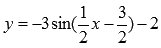
Решение.

Приводим функцию к виду шаблона :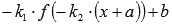

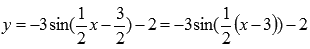
Имеем k1=3, k2=0,5, a=3, b=-2, причем перед коэффициентом k1 стоит знак «минус», перед k2 минуса нет.

Таким образом, цепочка преобразований графика функции y=sinx примет вид:

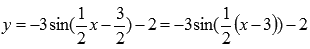
Поэтапное преобразование графика синусоиды. Графическая иллюстрация.

График исходной синусоиды y=sin(x) . Наименьший положительный период равен 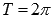. Максимумы находятся в точках 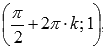, минимумы – в точках .

 

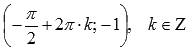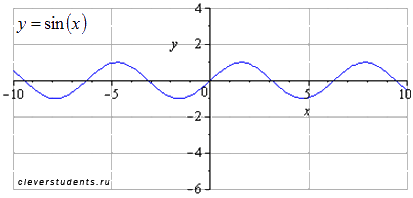
Растягиваем вдоль оси ординат втрое (амплитуда колебаний при этом возрастает в три раза). Наименьший положительный период равен 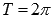. Максимумы переходят в точки 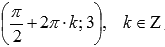, минимумы – в точки .

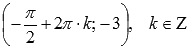Растягиваем вдоль оси абсцисс вдвое. Наименьший положительный период при этом вдвое увеличивается 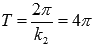. Максимумы переходят в точки 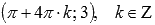, минимумы – в точки .

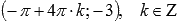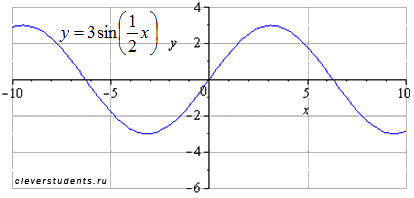
Симметрично отображаем относительно оси абсцисс. Наименьший положительный период при этом не меняется 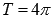. Максимумы переходят в точки 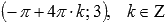, минимумы – в точки .

 

 

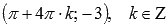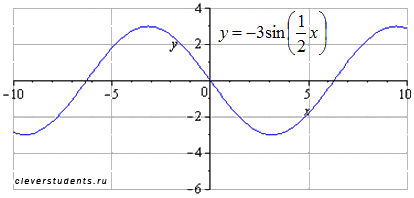Сдвигаем график вправо на 3 единицы. Наименьший положительный период при этом не меняется 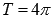. Максимумы переходят в точки 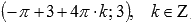, минимумы – в точки .

 

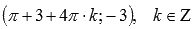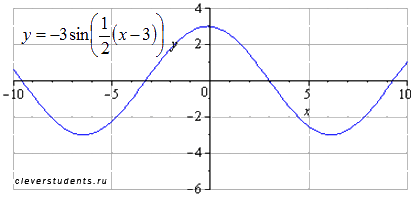Сдвигаем график вниз на 2 единицы. Наименьший положительный период при этом не меняется 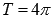. Максимумы переходят в точки 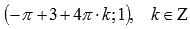минимумы – в точки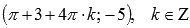

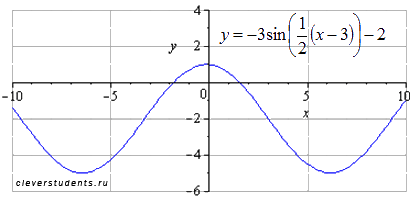Этим этапом задача преобразования графика тригонометрической функции y=sinx завершается.

 

Пример (преобразование тригонометрической функции y=cosx).

Построить график функции 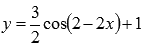преобразованием косинусоиды y=cosx.

Решение.

Приводим функцию к виду шаблона :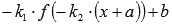

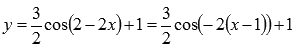
Имеем 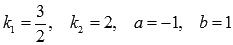, причем перед коэффициентом k2 стоит знак «минус», перед k1 минуса нет.

Таким образом, цепочка преобразований графика тригонометрической функции косинус примет вид:

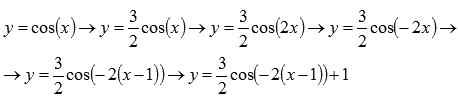
Поэтапное преобразование графика косинусоиды. Графическая иллюстрация.

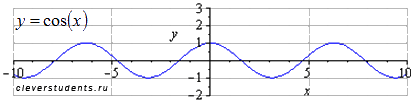
Исходный график y=cos(x) . Наименьший положительный период равен 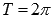. Максимумы находятся в точках 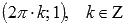, минимумы – в точках .

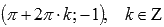Растягиваем вдоль оси ординат в 3/2 раза (амплитуда колебаний при этом возрастает в 3/2 раза). Наименьший положительный период равен 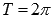. Максимумы переходят в точки 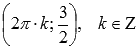, минимумы – в точки .

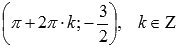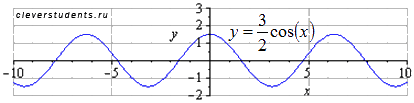
Сжимаем график вдоль оси абсцисс вдвое. Наименьший положительный период при этом вдвое уменьшается 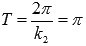. Максимумы переходят в точки 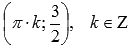, минимумы – в точки .

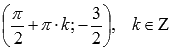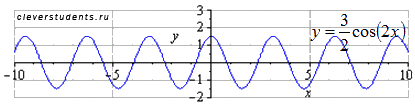
Симметрично отображаем относительно оси ординат. В силу четности функции график при этом не изменится.

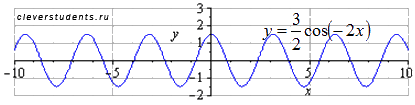Сдвигаем график вправо на 1 единицу. Наименьший положительный период при этом не меняется 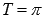. Максимумы переходят в точки 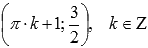, минимумы – в точки .

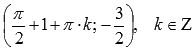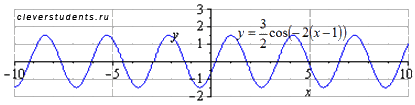
Сдвигаем график вверх на 1 единицу. Наименьший положительный период при этом не меняется 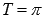. Максимумы переходят в точки 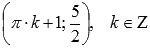, минимумы – в точки .

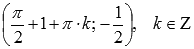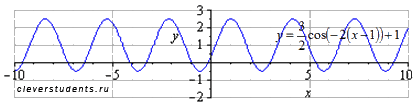
Этим этапом задача преобразования графика тригонометрической функции y=cosx завершается.

Пример (преобразование тригонометрической функции y=tgx ).

С помощью геометрических преобразований графика функции y=tgx построить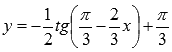

Решение.

Приводим функцию к виду шаблона :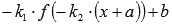

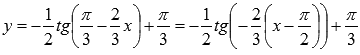
Имеем 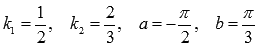, причем перед коэффициентами k1 и k2 стоит знак «минус».

Таким образом, цепочка преобразований графика тангенсоиды примет вид:

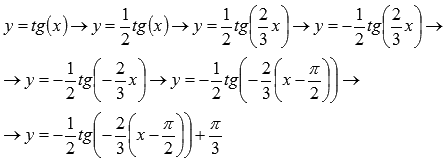
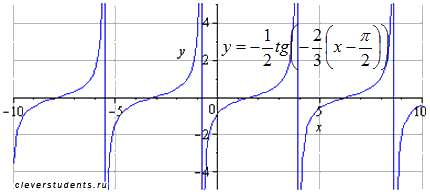
Поэтапное преобразование графика тангенсоиды. Графическая иллюстрация.

Исходный график y=tg(x) . Наименьший положительный период равен 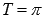. Область определения .

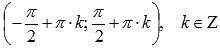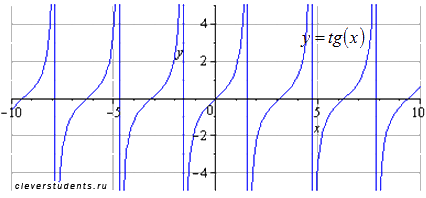
Производим сжатие вдоль оси ординат в 2 раза. Наименьший положительный период при этом не меняется 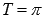. Область определения остается прежней .

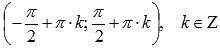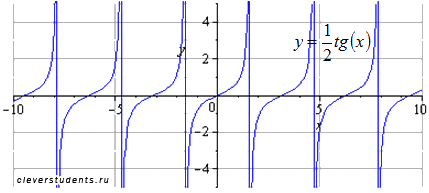
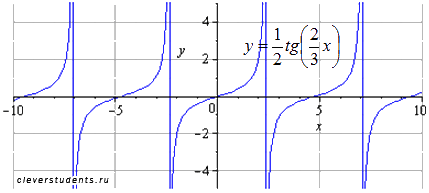
Растягиваем график вдоль оси абсцисс в 3/2 раза. Наименьший положительный период при этом равен 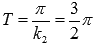. Область определения изменяется на .

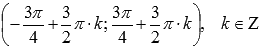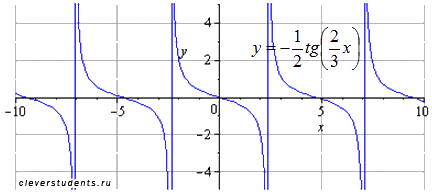
Симметрично отображаем относительно оси абсцисс. Период и область определения при этом не меняются.

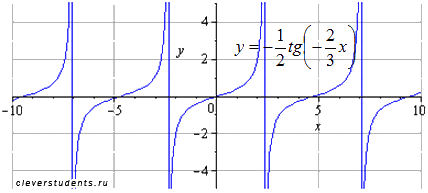
Симметрично отображаем относительно оси ординат. Период и область определения при этом не меняются. Стоит заметить, что график в точности совпадает с графиком двумя шагами ранее. Это объясняется нечетностью функции тангенса. То есть, если к нечетной функции применить симметричное отображение относительно осей ox и oy , то получим исходную функцию.

Сдвигаем график вправо на 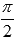(примерно на полторы единицы). Наименьший положительный период при этом не меняется 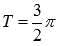Область определения изменяется на .

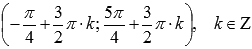Сдвигаем график вверх на 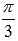(примерно на единицу). Период и область определения при этом не меняются.

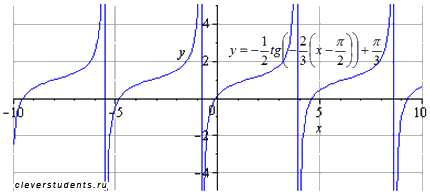
Этим этапом задача преобразования графика тригонометрической функции y=tgx завершается.

Пример (геометрические преобразования обратной тригонометрической функции y=arccosx).

Построить график функции преобразованием графика y=arccosx.

Решение.

Сначала от арккосинуса перейдем к арксинусу, используя соотношение обратных тригонометрических функций

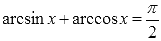
Следовательно,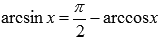

Таким образом, имеем цепочку преобразований арккосинуса в арксинус:

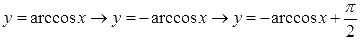
Поэтапное преобразование графика арккосинуса. Графическая иллюстрация.

Исходный график y=arccos(x) .

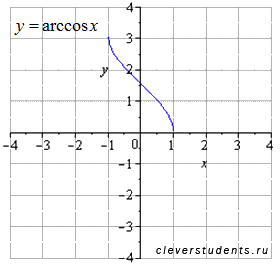
Отображаем симметрично относительно оси ox .

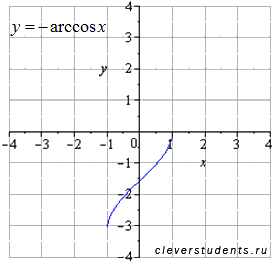
Сдвигаем вверх на .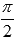

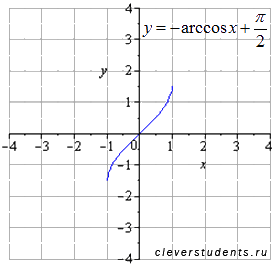
Вот так перешли от арккосинуса к арксинусу

Теперь проводим геометрические преобразования графика арксинуса.

Имеем 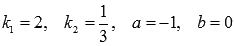, причем перед коэффициентами k1и k2 знака минуса нет.

Таким образом, цепочка преобразований графика y=arcsinx примет вид:

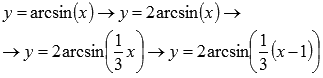
Поэтапное преобразование графика арксинуса. Графическая иллюстрация.

График функции y=arcsinx . Область определения 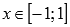. Область значений .

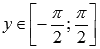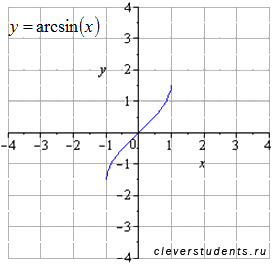
Растягиваем вдвое вдоль оси ординат. Область определения не меняется 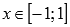. Область значений становится .

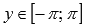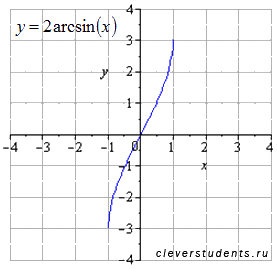
Растягиваем вдоль оси абсцисс втрое. При этом область определения расширяется до 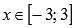. Область значений не меняется .

 

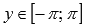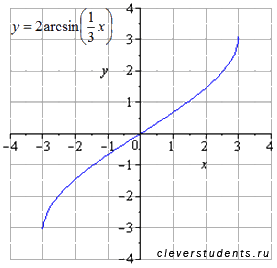
Сдвигаем график на единицу вправо. При этом область определения переходит в 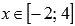. Область значений не меняется .

 

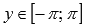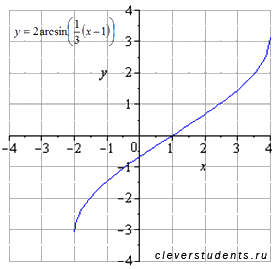Этим этапом задача преобразования графика обратной тригонометрической функции завершается.

Свойства степенной функции с четным положительным показателем.

◦Область определения: x ? (-∞;+∞)

◦Область значений: y ? [0;+∞)

◦Функция четная, так как y(-x)=y(x).

◦Функция возрастает при x ? [0;+∞)., убывает при x ? (-∞;0]

◦Функция вогнутая при x ? (-∞;+∞).

◦Точек перегиба нет.

◦Асимптот нет.

◦Функция проходит через точки (-1;1) , (0;0) , (1;1) .

III.Пусть а=-1, -3, -5, …

В этом случае график степенной функции будет иметь вид:

В качестве примера взяты а=-9 – черная линия, а=-5 – синяя линия, а=-3 – красная линия, а=-1 – зеленая линия. При а=-1 имеем обратную пропорциональность ( гиперболу ) - частный случай степенной.