У цьому випадку структура об'єкта моделювання опишеться графом, вершинами якого будуть елементи об'єкта, що описуються простими математичними моделями, а ребрами — їх зв'язки. Тоді математична модель об'єкта може бути отримана за допомогою цього графа, якщо існують математичні залежності, що описують його елементи та зв'язки між ними. Вхідні дуги кожної вершини визначають для неї вектор вхідних параметрів X, а вихідні — вектор вихідних показників Y.

Для побудови таких моделей використовують полюсні графи, які задають математичний опис елементів та зв'язків між ними:

•полюсні рівняння, що описують індивідуальні властивості кожного елемента;

•рівняння зв'язків, які відображають характер з'єднання елементів незалежно від їх властивостей.

Рівняння, що описують елементи моделі, називають полюсними, або компонентними. Компонентні рівняння отримуються шляхом експериментального або аналітичного дослідження та математичного моделювання простих елементів. Кожен елемент подається у вигляді двополюсника, що має один вхід і один вихід, тобто два полюси, а об'єднання моделей елементів між собою відбувається за допомогою об'єднання полюсів. Модель елемента описує залежність між двома параметрами, що характеризують стан елемента, у вигляді

.

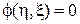Із двох параметрів, що описують елемент моделі, один буде вхідним ξ, що характеризує стан елемента відносно його полюсів, а інший — вихідним η, що характеризує реакцію елемента на зміну вхідного параметра. Елементи електричного кола (опір, ємність, індуктивність), наприклад, характеризуються залежністю між струмом та напругою, а елементи механічних систем — залежностями між силою та швидкістю.

Рівняння зв'язку — це, звичайно, фізичні закони, що відображають умови рівноваги та неперервності, наприклад, це закони Кірхгофа для електричних кіл або принцип Даламбера для механічних систем. Але за загальним правилом рівняння зв'язку повинні мати ті самі величини, що й полюсні, інакше моделі елементів не зможуть об'єднатися в загальну модель.

Для більшості технічних систем можна виділити три типові функціональні елементи: елемент розсіювання енергії R, елемент накопичення потенціальної енергії С та елемент накопичення кінетичної енергії L. Залежно від характеру технічного об'єкта, для якого створюється модель, розрізняють такі типові елементи та їх параметри:

для електричних систем елементами виступають електричний опір R, індуктивність L, ємність С, вхідним параметром яких є напруження U, а реакцією — електричний струм I. Ці елементи описуються за допомогою вхідних і вихідних параметрів:

; ; ;

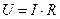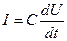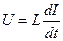для механічних систем елементами виступають маса М як елемент, що накопичує кінетичну енергію, в'язке тертя R як елемент, що розсіює енергію, пружність С як елемент, що накопичує потенціальну енергію, вхідним параметром яких є переміщення х або швидкість ν (для динамічних систем), а вихідним — сила F. Ці елементи описуються за допомогою залежностей:

; ; ;

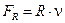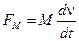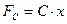або для останнього виразу

; ;

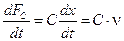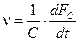для технологічних систем вхідним елементом виступає різниця потенціальних рівнів U як витрати енергії на одиницю перетвореного продукту, а вихідним — об'єм перетвореного продукту Q.

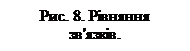
Рівняння зв'язку відображають характер з'єднання елементів незалежно від їх індивідуальних властивостей. Вони являють собою фізичні закони, що задають умови рівноваги та неперервності. Оскільки в технічному об'єкті не повинна накопичуватися енергія, а тільки перетворюватися, то загальними рівняннями зв'язку

між елементами моделі будуть наведені нижче:

1. Алгебрична сума вихідних параметрів у будь-якій вершині графа
дорівнює нулю (рис. 8, а):

.

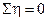Параметр вважається додатним, якщо він за напрямом виходить із вершини, або від'ємним — якщо спрямований у вершину. Для електричних об'єктів цей принцип відомий за назвою першого закону Кірхгофа (сума всіх струмів у вузлах схеми дорівнює нулю, 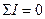), для механічних — принципу Даламбера (сума сил, що діють на тіло, дорівнює нулю, 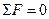). Для технологічних систем цей принцип полягатиме в тому, що сума витрат продукту в будь-якому розгалуженні технологічної системи дорівнює нулю, .

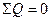2. У будь-якому замкнутому контурі графа алгебрична сума вхідних
параметрів дорівнює нулю:

.

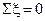Вхідні параметри вважаються додатними (рис. 8, б), якщо їх напрями збігаються з обраним напрямом обходження контуру, або від'ємними — якщо протилежні. Для електричних об'єктів цей принцип відомий за назвою другого закону Кірхгофа (сума спадів напруги в довіль­ному контурі схеми дорівнює нулю, тобто 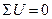), для механічних — принципу складання швидкостей, коли 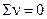. Для технологічних систем сума різниць рівнів потенціалів у кожному контурі дорівнює нулю, тобто .

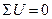Застосуємо розглянуті положення для теоретичного аналізу технічного об'єкта — механічної поступальної системи, елементами моделі якого є маса М, в'язке тертя R, пружність С, із вхідним параметром — швидкістю v та вихідним — силою F. Модель механічної системи доповнюється елементами, що описують джерела механічної енергії, тобто джерела вхідного чи вихідного параметрів. Це може бути джерело швидкості або джерело сили, які позначаються відповідними двополюсниками (рис. 9).

Використовуючи ці елементи, можна побудувати схему механічних зв'язків поступальної системи. Ця схема задасть зв'язки між простими моделями, що описують ці елементи.

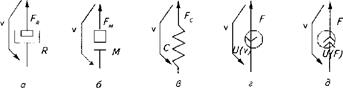
Рис. 9. Елементи опису динаміки механічних поступальних систем: а — тертя; б — маса; я — пружність; г — джерело швидкості; д — джерело сили

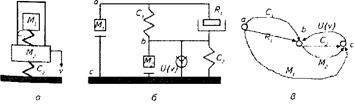
Побудуємо модель, що описує поведінку механічної поступальної системи в вертикальному напрямі (рис. 10, а). Ця система складається із платформи масою М₂, що рухається зі швидкістю v. Спочатку побудуємо еквівалентну схему механічної системи (рис. 10, б), а потім перейдемо від неї до графа зв'язків у моделі. В цьому графі з'єднання компонентів схеми опишуться вершинами, а ребра зададуть самі компоненти (рис. 10, в). Побудова моделі завершується застосуванням правил зв'язку, які описують умови рівноваги та неперервності для вхідних і вихідних параметрів.

		Рис. 10. Механічна система (а), її еквівалентна схема (б) та граф зв'язків між компонентами моделі (в).