Реальні технічні системи діють в умовах випадкових збурень, джерелами яких є як впливи зовнішнього середовища, так і відхилення різних характеристик технічної системи. Сукупність усіх параметрів зовнішнього середовища, які діють на технічну систему, поділяється на групи залежно від їх впливу на функціонування технічної системи: вхідні параметри, які описують дію зовнішнього середовища на технічну систему, задаються множиною Х. Вихід — це дія системи на зовнішнє середовище. Сукупність усіх вихідних параметрів утворює множину Y.

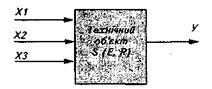
Рис. 5. Параметри, що описують стан технічної системи.

Стан об'єкта дослідження може бути описаний множинами параметрів, у яких виділимо такі підмножини (рис. 5):

вхідні параметри, або фактори Х, які характеризують вплив зовнішнього середовища на системний об'єкт дослідження, які розбиваються на три підмножини, а саме:

X1— керовані й вимірюва­ні величини, значення яких при дослідженні можна задати й кількісно визначити, наприк­лад, температура і час нагрівання зразка, швидкість переміщення, швидкість різання при механічній обробці. При проектуванні та оптимізації технічної системи вони називаються також елементами рішення;

Х2 — не керовані, але вимірювані величини, або обмежувальні вхідні величини, значення яких можна виміряти, але не можна задати. Це, наприклад, величина припуску на заготовці, питома вага матеріалу, його теплопровідність, концентрація домішок у вихідних матеріалах. При проектуванні та оптимізації технічної системи до них належать умови розподілу ресурсів та економічні критерії;

ХЗ— збурювальні величини, які впливають на процес функціонування, однак не можуть бути ні виміряні, ні цілеспрямовано змінені, наприклад, зношування з'єднань в обладнанні, його старіння, вібрації, зміщення налагоджених режимів;

вихідні параметри, що характеризують реакцію системи на зовнішні впливи, які утворюють вектор Y;

внутрішні параметри об'єкта 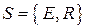, які описують елементи системи Ета зв'язки між ними R.

Розподіл зовнішніх впливів на суттєві та несуттєві є відносним, він залежить від досвідченості виконавця та мети дослідження. Наприклад, досліджуючи вільне падіння тіл, Галілео Галілей вважав опір повітря несуттєвим впливом, тоді як при дослідженні руху швидкісного літака чи ракети опір повітря вже не може належати до несуттєвих впливів.

Урахування суттєвих впливів має визначальне для вірогідності результатів дослідження значення. Якщо якийсь із суттєвих впливів не буде врахований, то результати дослідження можуть бути неповними або просто помилковими. Процес урахування суттєвих впливів значно спрощується, якщо дослідження базується на добре розробленій теорії. Якщо ж такої теорії немає, то використовуються гіпотези, догадки, ідеї.

Таким чином, чим повніше враховано при дослідженні вплив зовнішнього середовища на об'єкт дослідження, тим вища якість наукового дослідження.

Функція технічної системи

Будь-яка технічна система може функціонувати неперервно, виконуючи свою службову функцію упродовж тривалого часу, наприклад, хімічно-технологічні переробні системи, електроенергетичні системи. Доменні печі для виробництва чавуну. Це неперервні технічні системи.

На відміну від неперервних технологічних систем, у машинобудівному, приладобудівному, пакувальному та інших виробництвах широко застосовуються дискретні технологічні системи, особливістю яких є відносно короткий робочий цикл. Процес функціонування дискретної технічної системи являє собою багаторазову реалізацію технічної функції (ознака "технічної" введена для відмінності від математичної функції). Особливістю функціонування цих систем є сильний вплив випадкових збурень на результат реалізації технічної функції. Цей результат при кожній реалізації може набувати значення, відмінного від попередніх, тобто відбувається розпорошування показників реалізації технічної функції. Зокрема, якщо дискретна технічна система є промисловим роботом, який повинен подавати по одній деталі в задане місце, то показником реалізації технічної функції може бути вибрана похибка позиціонування, тобто різниця заданого та дійсного положень деталі. При тривалому функціонуванні промислового робота кожна з поданих деталей буде займати положення, що характеризуватиметься різними значеннями похибок позиціонування, які зумовлені тепловими, вібраційними, інерційними та іншими факторами збурення.

Тому для аналізу процесу функціонування дискретних технологічних систем доцільно використати апарат теорії випадкових процесів. Символічно технічна функція являє собою оператор технічної системи L. На технічний об'єкт діє зовнішнє середовище, вплив якого опишеться вектором вхідних параметрів X Результатом цієї дії буде реакція технічної системи, що опишеться вектором вихідних параметрів Y. Оператор L задає ті операції, які необхідно здійснити над вхідним вектором X, щоб отримати заданий вихідний вектор Y. При тривалому функціонуванні технічної системи ця технічна функція реалізується багато разів, а значення вхідного і вихідного векторів опишуться вхідною і вихідною математичними функціями Х(t), Y(t). Оскільки технічна функція реалізується в однакових умовах багато разів, то дія випадкових збурень призводить до того, що як вхідна X(t) так і вихідна Y(t) функції можуть бути віднесені до випадкових.

Тоді задача проектування технічної системи полягатиме в тому, щоб за заданими ймовірнісними характеристиками випадкової функції Х(t), що надходить на вхід технічної системи, визначити цю технічну систему, тобто її оператор L та конструкцію, яка забезпечує реалізацію цього оператора, таким чином, щоб функція Y(t), що отримається на виході, якнайкраще апроксимувала задану Y₀(t). Для точного формулювання цієї задачі визначимо, що слід розуміти під найкращою апроксимацією функції Y(t) на виході технічної системи. Багаторазове спрацьовування технічної системи при тривалому функціонуванні в приблизно однакових умовах створює множину подій, які мають статистичну однорідність, що забезпечує ймовірнісний характер наближення реалізованої функції Y(t) до заданої чи бажаної функції Y₀(t).

Найкращим наближенням можна вважати таке, при якому ймовірність того, що різниця між заданою функцією Y₀(t) та реалізованою Y(t) була б мінімальною

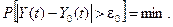
Найкращим наближенням можна також вважати таке, при якому математичне сподівання абсолютної величини різниці між показниками заданої та реалізованої функцій було б мінімальним, тобто

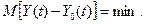
Найбільш простим критерієм наближення реалізованої функції до заданої можна вважати такий, який забезпечує мінімум математичного сподівання квадрата цієї різниці

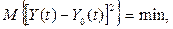
який може бути поданий у вигляді двох умов:

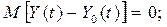
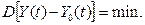
Дійсно, якщо показники випадкової функції Y(t) розподілені за нормальним законом, цей критерій задовольняє всі розглянуті вимоги, бо тоді різниця 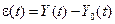є також нормальною величиною із математичним сподіванням 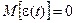та дисперсією 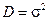, а ймовірність того, що різниця показників перевищить задане значення ε₀ становитиме

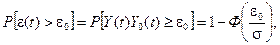
де Ф(x) — інтегральна функція Лапласа.

Розглянемо задачу визначення функціональної точності технічної системи для випадку, коли її технічна функція характеризується одним показником y. Це може бути лінійний розмір при обробці (технічна система — металорізальний верстат), маса продукту при фасуванні (технічна система — дозатор) тощо. Необхідно визначити ймовірність того, що упродовж заданого часу функціонування технічної системи параметр y не перевищить допустиму межу (в наведених прикладах технічної системи така межа задасться технічними вимогами на точність деталі чи на точність маси фасованого продукту). Якщо процес багаторазової реалізації показника технічної функції зобразити як випадкову Функцію, то наша задача зведеться до відомої в теорії випадкових функцій задачі про викиди випадкової функції за заданий рівень.

Нехай Y(t) — диференційований випадковий процес найбільш загального вигляду. Нехай y_м — задане максимальне значення ординати функції Y(t), викиди за яке є об'єктом дослідження.

Визначимо ймовірність того, що в нескінченно малому проміжкові часу dt, що безпосередньо настав після моменту часу t, відбудеться викид. Для цього необхідно, щоб відбулися дві події, а саме: в момент t ордината випадкової функції була б менше y_м, тобто y(t)< у у момент (t + dt) ордината випадкової функції повинна бути більше y_м, тобто 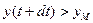. Тоді ймовірність викиду в інтервалі часу dt запишеться як 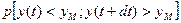. Врахувавши диференційованість функції отримаємо

,

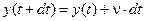де .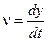

Тоді нерівність 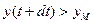перетвориться як 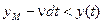, що дає ймовірність викиду

.

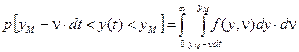У виразі використано двовимірний закон розподілу ординати випадкової функції та її похідної в один і той же момент часу t.

Оскільки інтервал інтегрування внутрішнього інтеграла дуже вузький, тобто дорівнює безмежно малому значенню ν·dt, то на основі теореми про середнє отримаємо

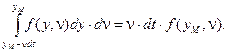
Тоді ймовірність викиду визначиться як

,

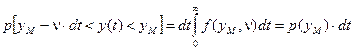де р(у_м) — ймовірність викиду за рівень у_M в момент часу t, обчислена на одиницю часу, яку також називають часовою щільністю ймовірності викиду.

Аналогічно можна обчислити і часову щільність ймовірності перетину випадковою функцією рівня y_m зверху вниз, яку позначимо як р(у_m). Тоді ймовірність викиду за верхню та нижню межі набуде вигляду

.

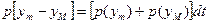Як бачимо, ймовірність викиду в нескінченно малому інтервалі часу А пропорційна величині цього інтервалу. Для знаходження чисельних оцінок часових щільностей для ймовірностей викиду необхідно дослідити й побудувати модель процесу функціонування технічної системи для знаходження значень р(у_т) та р(у_M).

Моделювання технічної системи

Будь-яка проектна та дослідницька діяльність так чи інакше пов'язана з побудовою моделі. Модель — це об'єкт будь-якої природи, який замінює із деяким ступенем точності досліджуваний об'єкт. Саме наявність етапу математичного моделювання є науковою основою процесу проектування. Хоча як процес дослідження, так і процес проектування оперують моделями, однак вони принципово відрізняються за характером відношення між самим об'єктом і його моделлю. При науковому дослідженні об'єкт первинний, а його модель — вторинна. Водночас при проектуванні модель ще неіснуючого об'єкта є первинною, описуючи службову функцію майбутнього об'єкта, а побудований за цією моделлю об'єкт — вторинним (рис. 6). Тобто об'єкт проектування ще не існує, а його модель уже створена.

Моделі відображають певні характеристики об'єкта, необхідні для розв'язання проблеми. Передусім при проектуванні необхідно уявити функціонування майбутньої технічної системи, зіставити її функціональні можливості з ресурсами та обмеження на них. Саме завдання проектування чи вдосконалення технічних об'єктів висувають вимоги до якості математичних моделей опису цих об'єктів.

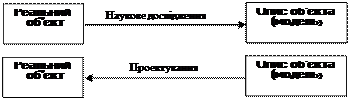В основу моделювання покладено метод аналогії, що ґрунтується на подібності деяких сторін різних предметів та явищ. За аналогією, умовивід як метод наукового пізнання дає змогу здобувати знання про одні предмети та явища на основі їх подібності до інших.

Рис. 6. Зв'язок між об'єктом і його моделлю під

час наукового дослідження та проектування.

Моделювання — метод наукового пізнання, що полягає в заміні об'єкта дослідження на спеціально побудований аналог, який відображає ті особливості об'єкта, які цікавлять дослідника. Цей аналог називається моделлю. Моделі поділяються на фізичні, які зберігають природу модельованих явищ чи предметів, та символічні, які описують об'єкт тією чи іншою мовою із відповідним рівнем формалізації (словесно-описові, графічні, математичні). Найбільш високий рівень формалізації забезпечують математичні моделі, які за допомогою математичних залежностей описують характеристики об'єкта, що вивчаються.

Побудова математичної моделі є результатом наукового дослідження. Від якості створеної математичної моделі залежить майбутнє проектованої технічної системи, бо така математична модель повинна, з одного боку, досить повно відобразити її основні характеристики, а з іншого — бути простою і зручною для використання при проектуванні. Цей опис повинен відобразити саме ті аспекти об'єкта — технічної системи, які цікавлять проектанта. Тому ступінь деталізації моделі, її форма визначаються загальною метою створення технічної системи. Правильно побудована математична модель враховує тільки ті фактори, внесок яких у явище чи процес, що вивчається, буде суттєвим.

Математичні моделі можуть бути побудовані шляхом вивчення та формалізації дослідного матеріалу, конструювання моделей складних процесів і технічних систем із відомих моделей їх елементів, отримання моделей простих об'єктів із опису більш загальних та складних.

Моделювання технічних об'єктів і процесів, які є результатом цілеспрямованого проектування, спрощується передусім завдяки заданості їх структури. Розглянемо приклади моделювання при різних рівнях відображення структури об'єкта моделювання в структурі його моделі.

1. Побудова моделі без вивчення структури об'єкта (об'єкт-"чорна скринька").

У цьому випадку при моделюванні не беруться до уваги внутрішні параметри. Математична модель описує зв'язок між зовнішніми параметрами:

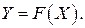
Якщо дія зовнішнього середовища на технічний об'єкт, наприклад, описується вектором X, що складається із трьох факторів х1, х2, х3, а результат цієї дії визначиться вектором-показником Y(y1,y2,y3), то модель матиме такий вигляд:

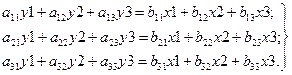
Розв'язання цієї системи рівнянь дає змогу перейти до складових простих моделей, що описують технічний об'єкт:

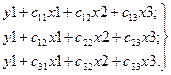
Для компактності застосовується форма запису у вигляді матриці

,

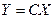де матричні елементи залежності мають такий вигляд:

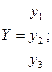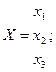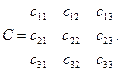
Така модель не описує внутрішню структуру технічного об'єкта, тому вона використовується для опису елементів структури.