Целью лабораторной работы является изучение основных понятий теории информации, некоторых способов кодирования информации, а также идей оптимального и помехозащищенного кодирования.
Требования к содержанию, оформлению и порядку выполнения
Отчет по выполнению лабораторной работы должен содержать: титульный лист, название работы, цель работы и содержательную часть (далее будем рассматривать требования только к содержательной части).
В содержательной части отчета по выполнению лабораторной работы требуется отразить процесс построения оптимальных кодов, расчет энтропии и средней длины оптимального кода для своего варианта. Также требуется сделать вывод о соотношении средней длины кода и энтропии.
Если выполнены дополнительные задания, то эти результаты также следует представить в отчете.
Теоретическая часть
Теоретические сведения, необходимые для выполнения лабораторной работы представлены в разд.2.2 и 2.3.
Общая постановка задачи
В лабораторной работе требуется построить оптимальные коды для восьми сообщений, если заданы вероятности появления каждого из сообщений. Посчитать энтропию и среднюю длину оптимального кода. Варианты заданий представлены в виде таблицы в следующем разделе.
В качестве дополнительных заданий рекомендуется выполнить следующее:
1. Реализовать алгоритм, представленный блок-схемой на рис.2.3. Указание: для реализации алгоритма использовать любой алгоритмический язык высокого уровня.
2. Реализовать алгоритм, представленный блок-схемой на рис.2.4. Указание: для реализации алгоритма использовать любой алгоритмический язык высокого уровня. Если в языке есть битовые операции, то обращение целого i в набор 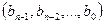 осуществить как с помощью операций целочисленного деления, получения остатка от деления, так и с помощью битовых операций, причем желательно предложить различные варианты использования битовых операций для реализации данного обращения.
осуществить как с помощью операций целочисленного деления, получения остатка от деления, так и с помощью битовых операций, причем желательно предложить различные варианты использования битовых операций для реализации данного обращения.
3. Построить графики времени работы алгоритмов, реализованных в пунктах 1 и 2. Указание: оба графика построить в одной системе координат. По оси Y откладывать время работы алгоритма, по оси X длину кода. Время работы алгоритма измерять с помощью функций времени используемого языка программирования. При этом выдавать на экран время начала и конца работы алгоритма, вывод кодов заблокировать. Длину кода менять. Рассматривать только те длины кода, при которых время работы алгоритмов составляет не менее одной секунды. Для построения графиков можно воспользоваться системой Excel.
4. Реализовать алгоритм, представленный блок-схемой на рис.2.5. Указание: для реализации алгоритма использовать любой алгоритмический язык высокого уровня.
5. Доработать алгоритмы реализованные в пунктах 1,2 и 4 так, чтобы к каждому кодовому слову добавлялся бит четности.
Список индивидуальных данных
Данные для выполнения лабораторной работы сведены в табл.Л1.1.
| Таблица Л1.1 | ||||||||
| Варианты заданий лабораторной работы №1 | ||||||||
| Вариант | Вероятности появления сообщений | |||||||
| m1 | m2 | m3 | m4 | m5 | m6 | m7 | m8 | |
| 0,04 | 0,17 | 0,279 | 0,158 | 0,07 | 0,191 | 0,009 | 0,083 | |
| 0,347 | 0,014 | 0,0673 | 0,291 | 0,0986 | 0,084 | 0,053 | 0,0451 | |
| 0,185 | 0,058 | 0,0692 | 0,198 | 0,191 | 0,183 | 0,014 | 0,1018 | |
| 0,279 | 0,091 | 0,0174 | 0,383 | 0,0571 | 0,0936 | 0,0371 | 0,0418 | |
| 0,291 | 0,096 | 0,285 | 0,183 | 0,001 | 0,0267 | 0,01 | 0,1073 | |
| 0,311 | 0,081 | 0,0391 | 0,451 | 0,013 | 0,0281 | 0,0537 | 0,0231 | |
| 0,0971 | 0,037 | 0,0992 | 0,476 | 0,281 | 0,001 | 0,0052 | 0,0035 | |
| 0,0879 | 0,071 | 0,0893 | 0,625 | 0,0021 | 0,0361 | 0,0632 | 0,0254 | |
| 0,0098 | 0,021 | 0,183 | 0,0271 | 0,691 | 0,00961 | 0,0439 | 0,01459 | |
| 0,029 | 0,041 | 0,291 | 0,039 | 0,555 | 0,0142 | 0,0181 | 0,0127 | |
| 0,471 | 0,039 | 0,0983 | 0,019 | 0,0381 | 0,142 | 0,0993 | 0,0933 | |
| 0,221 | 0,021 | 0,0895 | 0,4193 | 0,0481 | 0,0987 | 0,0879 | 0,0145 | |
| 0,003 | 0,039 | 0,0783 | 0,691 | 0,019 | 0,0921 | 0,0634 | 0,0142 | |
| 0,01 | 0,081 | 0,0894 | 0,391 | 0,291 | 0,099 | 0,0192 | 0,0194 | |
| 0,02 | 0,072 | 0,0832 | 0,0989 | 0,191 | 0,3891 | 0,117 | 0,0288 | |
| 0,043 | 0,051 | 0,0673 | 0,295 | 0,219 | 0,2732 | 0,0439 | 0,0076 | |
| 0,09 | 0,085 | 0,0582 | 0,318 | 0,229 | 0,216 | 0,0017 | 0,0021 | |
| 0,08 | 0,059 | 0,0482 | 0,719 | 0,0198 | 0,014 | 0,0272 | 0,0328 | |
| 0,07 | 0,0958 | 0,0938 | 0,1821 | 0,2393 | 0,307 | 0,0096 | 0,0024 | |
| 0,069 | 0,0781 | 0,193 | 0,3 | 0,0911 | 0,2111 | 0,0439 | 0,0138 | |
| 0,072 | 0,0272 | 0,295 | 0,0927 | 0,05892 | 0,3719 | 0,0673 | 0,01498 | |
| 0,031 | 0,087 | 0,382 | 0,381 | 0,0094 | 0,0927 | 0,0047 | 0,0122 | |
| 0,036 | 0,028 | 0,391 | 0,284 | 0,1927 | 0,0293 | 0,0297 | 0,0093 | |
| 0,072 | 0,358 | 0,317 | 0,00569 | 0,09156 | 0,068 | 0,0373 | 0,05045 | |
| 0,083 | 0,41 | 0,0629 | 0,01892 | 0,274 | 0,1 | 0,0321 | 0,01908 | |
| 0,047 | 0,0721 | 0,0849 | 0,438 | 0,1937 | 0,1321 | 0,0284 | 0,0038 | |
| 0,091 | 0,0632 | 0,029 | 0,791 | 0,0162 | 0,0082 | 0,000972 | 0,000428 | |
| 0,083 | 0,0563 | 0,257 | 0,372 | 0,1883 | 0,00592 | 0,02865 | 0,00883 | |
| 0,082 | 0,0761 | 0,374 | 0,0397 | 0,0869 | 0,3291 | 0,0087 | 0,0035 | |
| 0,091 | 0,0825 | 0,00928 | 0,03591 | 0,2689 | 0,00778 | 0,291 | 0,21363 |
Пример выполнения работы
Рассмотрим 30 вариант. Согласно заданию имеем восемь сообщений: 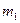 ,
, 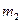 ,
, 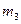 ,
, 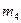 ,
, 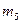 ,
, 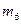 ,
, 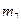 ,
, 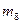 . Известна вероятность появления каждого из этих сообщений:
. Известна вероятность появления каждого из этих сообщений: 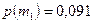 ;
; 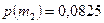 ;
; 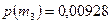 ;
; 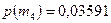 ;
; 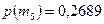 ;
; 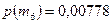 ;
; 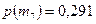 ;
; 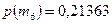 .
.
Вначале проверим правильность исходных данных. Проверим равенство 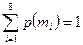 .
.
0,091+0,0825+0,00928+0,03591+0,2689+0,00778+0,291+0,21363=1
Построим оптимальные коды для данных восьми сообщений по алгоритму, рассмотренному в разд.2.3.4.
Разобьем исходные сообщения на две группы таким образом, чтобы сумма вероятностей в каждой группе была примерно одинакова. В результате в первую группу попадут сообщения 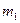 ,
, 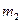 ,
, 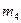 и
и 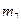 , а во вторую группу –
, а во вторую группу – 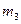 ,
, 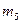 ,
, 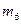 и
и 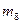 . Суммарная вероятность сообщений первой группы равна 0,091+0,0825+0,03591+0,291=0,50041. Суммарная вероятность сообщений второй группы равна 0,00928+0,2689+0,00778+0,21363=0,49959. Первую группу пометим символом 1, вторую группу – символом 0.
. Суммарная вероятность сообщений первой группы равна 0,091+0,0825+0,03591+0,291=0,50041. Суммарная вероятность сообщений второй группы равна 0,00928+0,2689+0,00778+0,21363=0,49959. Первую группу пометим символом 1, вторую группу – символом 0.
Первый шаг разбиения исходного множества сообщений проиллюстрирован на рис. Л1.1.
 |
Далее по тому же принципу разобьем сообщения 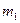 ,
, 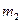 ,
, 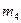 и
и 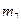 на две группы. В результате в первую группу попадут сообщения
на две группы. В результате в первую группу попадут сообщения 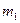 ,
, 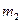 ,
, 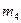 , а во вторую группу –
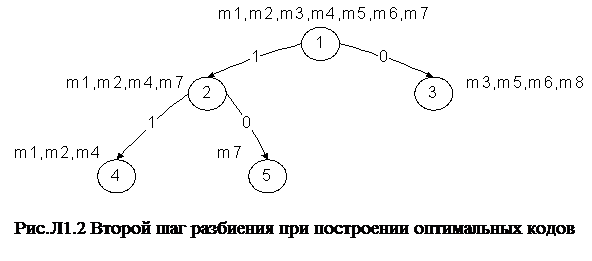
, а во вторую группу – 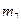 . Суммарная вероятность сообщений первой группы равна 0,091+0,0825+0,03591=0,50041. Вероятность сообщения m7 равна 0,291. Первую группу пометим символом 1, вторую группу – символом 0. Данный шаг разбиения проиллюстрирован на рис. Л1.2.
. Суммарная вероятность сообщений первой группы равна 0,091+0,0825+0,03591=0,50041. Вероятность сообщения m7 равна 0,291. Первую группу пометим символом 1, вторую группу – символом 0. Данный шаг разбиения проиллюстрирован на рис. Л1.2.
Выполним аналогичное разбиение сообщений 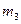 ,
, 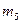 ,
, 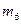 и
и 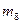 . В результате в первую группу попадет сообщение m5, а во вторую группу –
. В результате в первую группу попадет сообщение m5, а во вторую группу – 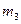 ,
, 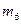 ,
, 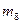 . Вероятность сообщения
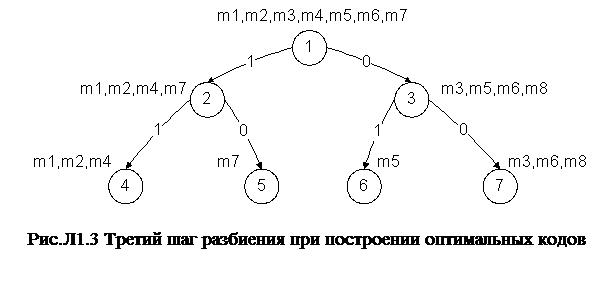
. Вероятность сообщения 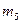 равна 0,2689. Суммарная вероятность сообщений второй группы равна 0,00928+0,00778+0,21363=0,23069. Первую группу пометим символом 1, вторую группу – символом 0. Данный шаг разбиения проиллюстрирован на рис.Л.1.3.
равна 0,2689. Суммарная вероятность сообщений второй группы равна 0,00928+0,00778+0,21363=0,23069. Первую группу пометим символом 1, вторую группу – символом 0. Данный шаг разбиения проиллюстрирован на рис.Л.1.3.
 |
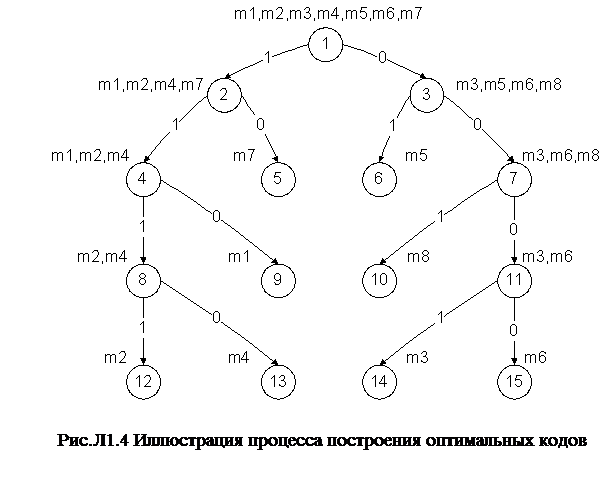
Продолжая процесс разбиения, окончательно получим дерево, представленное на рис.Л1.4.
Концевые вершины данного дерева соответствуют исходным сообщениям. Сообщению 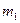 соответствует вершина 9,
соответствует вершина 9, 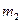 – 12,
– 12, 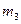 – 14,
– 14, 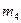 – 13,
– 13, 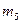 – 6,
– 6, 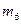 – 15,
– 15, 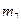 – 5,
– 5, 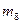 – 10. Для определения кода некоторого сообщения требуется найти путь из корня дерева (вершина 1) в вершину, соответствующую данному сообщению. Код образуют пометки дуг, образующих такой путь. Например, сообщение
– 10. Для определения кода некоторого сообщения требуется найти путь из корня дерева (вершина 1) в вершину, соответствующую данному сообщению. Код образуют пометки дуг, образующих такой путь. Например, сообщение 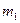 имеет код 110, который соответствует пути 1,2,4,9.
имеет код 110, который соответствует пути 1,2,4,9.
Коды сообщений сведены в таблицу Л1.2.
| Таблица Л1.2 | |||
| Оптимальные коды | |||
| Сообщение | Код сообщения | Сообщение | Код сообщения |
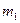
| 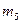
| ||
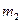
| 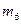
| ||
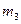
| 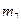
| ||
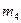
| 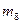
|
Итак, сообщение 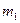 кодируется 3 битами,
кодируется 3 битами, 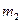 – 4 битами,
– 4 битами, 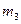 – 4 битами,
– 4 битами, 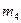 – 4 битами,
– 4 битами, 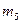 – 2 битами,
– 2 битами, 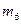 – 4 битами,
– 4 битами, 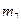 – 2 битами,
– 2 битами, 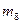 – 3 битами.
– 3 битами.
Определим среднее число бит, приходящихся на одно сообщение (n). 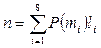 , где
, где 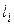 - число бит, требуемое для кодирования i-го сообщения.
- число бит, требуемое для кодирования i-го сообщения.
n= 0,091×3+0,0825×4+0,00928×4+0,03591×4+
0,2689×2+0,00778×4+0,291×2+ 0,21363×3=2,57557
Используя формулу 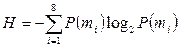 , найдем энтропию.
, найдем энтропию.
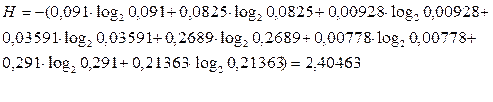
Вывод. В лабораторной работе получены оптимальные коды для восьми сообщений с заданными вероятностями, рассчитана средняя длина кода 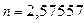 и количество информации, приходящееся на одно сообщение (энтропия
и количество информации, приходящееся на одно сообщение (энтропия 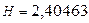 ).
).
Если при кодировании заданных восьми сообщений не учитывать их вероятности появления, то для кодирования каждого сообщения потребуется 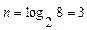 бита. Таким образом, мы получили более оптимальный код, в котором
бита. Таким образом, мы получили более оптимальный код, в котором 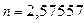 бит.
бит.
При используемом алгоритме оптимального кодирования значение n лежит в пределе от H до 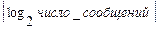 .
.
Контрольные вопросы к защите
1. Понятие информации.
2. Понятие сигнала. Дискретизация сигналов.
3. Чем руководствоваться при выборе частоты дискретизации непрерывного сигнала.
4. Понятие меры количества информации. Единицы измерения количества информации.
5. Понятие избыточности текста. Оценка избыточности текста.
6. Понятие удельной информативности (энтропии) сигнала.
7. Понятие кодирования информации. Кода. Основания и длины кода.
8. Определение оптимального основания кода.
9. Запись натуральных чисел в двоичной системе.
10. Рекурсивное определение последовательности кодовых слов в порядке двоичного счета.
11. Алгоритмы порождения кодовых слов в порядке двоичного счета.
12. Понятие кода Грэя, особенности данного кода.
13. Рекурсивное определение двоично-отраженного кода Грэя.
14. Задание кода Грэя начальным словом и последовательностью переходов.
15. Рекурсивное определение последовательности переходов двоично-отраженного кода Грэя.
16. Алгоритм порождения двоично-отраженного кода Грэя.
17. Суть идеи оптимального кодирования.
18. Алгоритм построения оптимальных кодов.
19. Суть идеи построения помехозащищенных кодов.
20. Код с проверкой на четность.
Способ оценки результатов
При оценке результатов выполнения лабораторной работы оценивается:
· знание программного материала;
· качество и количество выполненных дополнительных заданий определенных в разделе «общая постановка задачи»;
· грамотность и аккуратность оформления отчета по лабораторной работе;
· глубина и полнота ответов на контрольные вопросы.
Отметка «отлично» выставляется студенту, глубоко и прочно усвоившему программный материал, исчерпывающе, последовательно, грамотно и логически стройно его излагающему, выполнившему большинство дополнительных заданий, ответившему на все контрольные вопросы, грамотно и аккуратно оформившему лабораторную работу.
Отметка «хорошо» выставляется студенту, твердо знающему программный материал, грамотно и по существу его излагающему, имеющему представление о решении дополнительных заданий, ответившему на все контрольные вопросы, грамотно и аккуратно оформившему лабораторную работу.
Отметка «удовлетворительно» выставляется студенту, который знает только основной материал, но не усвоил его деталей, допускает в ответе неточности, имеющему расплывчатое представление о решении некоторых дополнительных заданий, ответившему на все контрольные вопросы, оформившему лабораторную работу с нарушением некоторых несущественных требований.
Отметка «неудовлетворительно» выставляется студенту, который не знает значительной части программного материала, допускает существенные ошибки, не имеет представление о решении ряда дополнительных заданий, не ответившему на контрольные вопросы, оформившему лабораторную работу с существенными нарушениями.
Дата: 2016-09-30, просмотров: 453.