При решении задач, связанных с расчетом количества информации, необходимо пользоваться теоретическим материалом, представленным в разд.2.2.

Для решения некоторых задач требуется пользоваться основной аксиомой комбинаторики - правилом произведения. В общем случае данное правило может быть сформулировано следующим образом.

Пусть требуется выполнить одно за другим k действий. Если первое действие выполнить 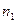способами, второе действие – 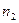способами, третье действие – 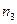способами и так до k действия, которое можно выполнить 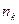способами, то все k действий могут быть выполнены 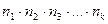способами.

Также при решении задач данной группы используются формулы (1) и (2), представленные в разд.2.2 и сведения, представленные в разделах 2.3.2-2.3.5, 3.3.

При решении задач, связанных с преобразованием отношений, используется материал, представленный в разд. 4.3.2.

Примеры решения типовых задач

Задача 1. Сколько двоичных разрядов потребуется для кодировки 14 различных сообщений, если каждое кодовое слово должно иметь одинаковую длину?

Решение. По формуле (1) имеем 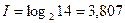бит, округляем это число до 4 (до ближайшего большего целого). Таким образом, 14 различных сообщений можно закодировать 4-мя двоичными разрядами. Точнее 4-мя двоичными разрядами можно закодировать 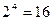различных сообщений, т.е. 2 кодовых слова останутся свободными.

Задача 2. Пусть имеется 64 кодовых знака. В слове длины 8 все кодовые знаки равновероятны. Сколько бит информации несет такое слово?

Решение. По формуле (2) имеем 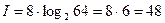бит.

Задача 3. Сколько товаров можно закодировать, если для кодировки используется трехразрядный код, причем первый разряд может принимать значения из множества {A,B,C}, а все остальные разряды заполняются цифрами десятичной системы.

Решение. Первый разряд можно заполнить тремя способами (A, B или C), второй разряд можно заполнить десятью способами (0,1,…,9), третий разряд также можно заполнить десятью способами. По правилу произведения число таких трехразрядных кодов будет равно 3∙10∙10 =300 штук, т.е можно закодировать 300 товаров.

Задача 4. Сколько сигналов можно передать по двухпроводной линии, если сигналы на каждом проводе могут принимать четыре различных значения.

Решение. На первом проводе сигнал может принимать четыре значения, на втором - также четыре значения. По правилу произведения число сигналов, которые можно передать по такой линии, будет равно 4∙4=16.

Задача 5. Пусть даны два отношения R1={(x,1),(w,3),(e,2),(x,4)} и R2={(x,1),(x,4),(y,5),(s,2)}. Чему равен результат выполнения операции объединения данных отношений?

Решение. Согласно определению операции объединения, имеем:

R1UR2={(x,1),(w,3),(e,2),(x,4),(y,5),(s,2)}

Задача 6. Пусть даны два отношения R1={(x,1),(w,3),(e,2),(x,4)} и R2={(x,1),(x,4),(y,5),(s,2)}. Чему равен результат выполнения операции пересечения данных отношений?

Решение. Согласно определению операции пересечения, имеем:

R1∩R2={(x,1),(x,4)}

Задача 7. Пусть даны два отношения R1={(x,1),(w,3),(e,2),(x,4)} и R2={(x,1),(x,4),(y,5),(s,2)}. Чему равен результат выполнения операции разности данных отношений?

Решение. Согласно определению операции разности, имеем:

R1\R2={(w,3),(e,2)}

Задача 8. Пусть даны два отношения R1={(x,1),(w,3)} и R2={(y,5),(s,2)}. Чему равен результат выполнения операции декартова произведения данных отношений?

Решение. Согласно определению операции декартова произведения, имеем:

R1ÄR2={(x,1,y,5),(x,1,s,2),(w,3,y,5),(w,3,s,2)}

Задача 9. Дано отношение R(A,B,C)= {(x,1,Q),(w,2,E),(e,2,M),(x,4,Q), (x,6,Q)}. Чему равен результат выполнения операции проекции R[A,C]?

Решение. Согласно определению операции проекции, имеем:

R[A,C]={(x,Q),(w,E),(e,M)}

Задачи для самостоятельного решения

1. Сколько двоичных разрядов потребуется для кодировки 58 различных сообщений, если каждое кодовое слово должно иметь одинаковую длину?

2. Сколько двоичных разрядов потребуется для кодировки 14 различных сообщений, если каждое кодовое слово должно иметь одинаковую длину?

3. Пусть имеется 16 кодовых знака. В слове длины 10 все кодовые знаки равновероятны. Сколько бит информации несет такое слово?

4. Пусть имеется 32 кодовых знака. В слове длины 4 все кодовые знаки равновероятны. Сколько бит информации несет такое слово?

5. Сколько различных сообщений можно передать по 7 проводам, если уровень сигнала на каждом проводе может принимать 2 значения?

6. Сколько различных сообщений можно передать по 4 проводам, если уровень сигнала на каждом проводе может принимать 3 значения?

7. Сколько различных сообщений можно закодировать с помощью 9 двоичных разрядов?

8. Сколько различных сообщений можно закодировать 5 разрядным словом, если каждый разряд может принимать 3 значения?

9. Пусть на предприятии для кодирования использующихся в производстве материалов применяется код длины 5. Первый элемент кода может быть буквой А или В, каждый из оставшихся четырех элементов может быть десятичной цифрой. Сколько всего материалов может быть закодировано таким кодом?

10. Пусть на предприятии каждому сотруднику присвоен код длины 4. В качестве элементов кода могут выступать символы множества {1,2,3,А,В}. Сколько всего сотрудников может быть закодировано таким кодом?

11. Пусть на предприятии каждому отделу присвоен код длины 3. В качестве первого элемента кода может выступать символ множества {А,В,С}. В качестве второго и третьего элементов кода может выступать десятичная цифра. Сколько всего отделов может быть закодировано таким кодом?

12. Пусть используется код с проверкой на четность. Чему равны проверочные разряды d и g кодовых слов a=(00011010d) и b=(9Ag)? Здесь для записи первых восьми бит кодового слова b использовалась шестнадцатеричная система.

13. Пусть используется код с проверкой на четность. Чему равны проверочные разряды d и g кодовых слов a=(11011000d) и b=(B1g)? Здесь для записи первых восьми бит кодового слова b использовалась шестнадцатеричная система.

14. Пусть используется код с проверкой на четность. Чему равны проверочные разряды d и g кодовых слов a=(01110001d) и b=(94g)? Здесь для записи первых восьми бит кодового слова b использовалась шестнадцатеричная система.

15. Пусть используется код с проверкой на нечетность. Чему равны проверочные разряды d и g кодовых слов a=(D3d) и b=(01100100g)? Здесь для записи первых восьми бит кодового слова a использовалась шестнадцатеричная система.

16. Пусть используется код с проверкой на нечетность. Чему равны проверочные разряды d и g кодовых слов a=(3Ed) и b=(00110110g)? Здесь для записи первых восьми бит кодового слова a использовалась шестнадцатеричная система.

17. Сколько двоичных разрядов потребуется для кодировки всех букв английского языка?

18. Сколько двоичных разрядов потребуется для кодировки всех букв русского языка?

19. Сколько различных сообщений можно передать с помощью 6 флажков различного цвета, взятых по два?

20. В книге Льюиса Кэррола расказывается, как героиня Алиса поняла, что для разговора с котенком вполне достаточно, чтобы он мурлыкал, когда хочет сказать «да» и мяукал, когда хочет сказать «нет». К сожалению, котенок мурлыкал в ответ на все вопросы. Сколько бит информации передавал Алисе котенок?

21. Допустим, что Вы забыли точный адрес вашего приятеля. Вам известна улица и номер дома. Но оказалось, что под данным номером значится два двухэтажных корпуса, в каждом корпусе два подъезда, в каждом подъезде по два этажа, на каждом этаже по две квартиры. Сколько бит информации Вам не достает, чтобы определить номер квартиры вашего приятеля?

22. Разработайте правила быстрого преобразования чисел, записанных в двоичной системе в соответствующие числа, записанные в восьмеричной системе. Также разработайте правила обратного преобразования, т.е. правила преобразования чисел, записанных в восьмеричной системе, в числа, записанные в двоичной системе. Разработайте аналогичные правила, только вместо восьмеричной системы используйте шестнадцатеричную систему счисления. Сделайте вывод, почему восьмеричная и шестнадцатеричная системы широко используются в программировании.

23. Определите избыточность 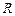некоторого иностранного текста и оцените свои знания языка по следующей шкале: 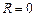- 0 баллов, 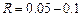- 2 балла, 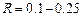- 3 балла, 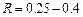- 4 балла и 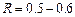- 5 баллов.

24. Примером устройства, содержащего аналого-цифровой преобразователь, является звуковая карта. Кроме того, в звуковой карте содержится устройство, осуществляющее обратное преобразование из цифровой информации в аналоговую информацию. Если используется 16-битная звуковая карта, то ее динамический диапазон не хуже, чем динамический диапазон CD, и качество звука определяется частотой дискретизации (частотой сэмплинга). Частота сэмплинга обычно выбирается программно. В зависимости от используемого ПО частота сэмплинга может быть следующей (Гц): 8000, 11025, 11127, 18900, 22050, 22255, 32000, 37800, 44056, 44100, 48000, 88200, 96000. Другим важным параметром является число каналов: один канал (моно) или два канала (стерео). Исследуйте, какая частота сэмплинга не вызывает у Вас неприятных слуховых ощущений. Объясните почему. Оцените расход памяти на секунду звучания для различных частот сэмплинга и для различных форматов звуковых файлов.

25. Сколько товаров может быть закодировано штрих-кодом в формате EAN-8, если для кодирования разрешено использовать все доступные разряды данного штрих-кода.

26. Сколько товаров может быть закодировано штрих-кодом в формате EAN-13, если для кодирования разрешено использовать все доступные разряды данного штрих-кода.

27. Сколько товаров может быть закодировано штрих-кодом в формате EAN-13, если шесть разрядов данного штрих-кода заняты для кодирования даты выпуска товара.

28. Сколько товаров может быть закодировано штрих-кодом в формате EAN-13, если шесть разрядов данного штрих-кода заняты для кодирования даты выпуска товара, и два разряда заняты для кодирования цеха, где был произведен товар.

29. Пусть даны два отношения R1={(a,2),(b,1),(c,8),(c,1)} и R2={(c,7),(a,2),(b,1)}. Чему равен результат выполнения операции объединения данных отношений?

30. Пусть даны два отношения R1={(a,1),(b,2),(c,3)} и R2={(b,2),(c,3),(d,2)}. Чему равен результат выполнения операции объединения данных отношений?

31. Пусть даны два отношения R1={(x,2),(x,3),(x,4)} и R2={(y,1),(y,2),(y,3)}. Чему равен результат выполнения операции пересечения данных отношений?

32. Пусть даны два отношения R1={(x,1),(w,3),(e,2),(x,4)} и R2={(x,1),(x,4)}. Чему равен результат выполнения операции пересечения данных отношений?

33. Пусть даны два отношения R1={(x,1),(w,3),(x,4)} и R2={(x,1),(y,5),(s,2)}. Чему равен результат выполнения операции разности данных отношений?

34. Пусть даны два отношения R1={(x,1),(x,2),(x,3),(x,4)} и R2={(x,1),(x,4),(y,5)}. Чему равен результат выполнения операции разности данных отношений?

35. Пусть даны два отношения R1={(x,1)} и R2={(y,5),(s,2)}. Чему равен результат выполнения операции декартова произведения данных отношений?

36. Пусть даны два отношения R1={(x,1),(w,3)} и R2={(y,5)}. Чему равен результат выполнения операции декартова произведения данных отношений?

37. Дано отношение R(A,B,C)={(x,1,Q),(x,1,E),(e,2,M),(x,4,Q)}. Чему равен результат выполнения операции проекции R[A,B]?

38. Дано отношение R(A,B,C)= {(x,2,Q),(w,4,E),(e,1,M),(x,2,Q),(x,6,Q)}. Чему равен результат выполнения операции проекции R[A,C]?

Практикум (лабораторный)