Цель работы: изучение методик выполнения и обработки экспериментальных данных прямых многократных и однократных измерений.
Задание:
1. Изучить теоретические материалы к лабораторной работе.
2. Выполнить многократные измерения.
3. Выполнить однократное измерение.
4. Обработать полученные экспериментальные данные.
5. Составить отчет по лабораторной работе.
Теоретические основы работы
Обработка экспериментальных данных прямых многократных измерений
Многократные измерения проводятся с целью уменьшения влияния случайных погрешностей на результат измерения. При многократных измерениях за измеренное значение величины принимается среднее арифметическое из всех полученных отдельных измерений.
В практике при обработке экспериментальных данных чаще всего приходится сталкиваться со случаями, когда число измерений мало (не превышает 5–15). В этих случаях пользуются вполне оправданным предположением о том, что закон распределения случайной погрешности является нормальным, а грубые погрешности не выявляются или определяются и отбрасываются интуитивно.
В соответствии с государственным стандартом обработка экспери-ментальных данных прямых многократных измерений базируется на теоретических положениях математической статистики, которые предпо-лагают определение вместо характеристик нормального распределения их оценок.
Первым параметром нормального закона распределения является математическое ожидание М(Х), то есть значение величины, вокруг которого группируются результаты отдельных измерений (при бесконечном числе измерений). Вместо математического ожидания М(X) определяется его оценка, которая представляет собой среднее арифметическое 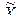 :
:
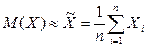 , (3.6)
, (3.6)
где Xi – результат i-го измерения; n – число измерений.
Второй параметр нормального закона распределения – средне-квадратическое отклонение (СКО) s, характеризующее рассеяние результатов отдельных измерений относительно математического ожидания, определяется оценкой по формуле
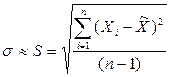 . (3.7)
. (3.7)
Оценка СКО результата измерений определяется по формуле
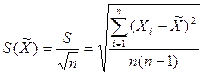 . (3.8)
. (3.8)
Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов.
Доверительным интервалом с границами (или доверительными границами) от – 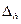 до +
до + 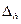 называют интервал значений случайной погрешности, который с заданной вероятностью Рд, называемой доверительной, накрывает истинное значение измеряемой величины. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интерва-лом и по нему определять доверительную вероятность (либо наоборот, по доверительной вероятности подсчитывать доверительный интервал). Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95.
называют интервал значений случайной погрешности, который с заданной вероятностью Рд, называемой доверительной, накрывает истинное значение измеряемой величины. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интерва-лом и по нему определять доверительную вероятность (либо наоборот, по доверительной вероятности подсчитывать доверительный интервал). Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95.
Так как нормальный закон распределения описывает поведение случайной погрешности в принципе при бесконечно большом числе измерений, а при малом числе измерений (n £ 20) и использовании нормального закона не представляется возможным определить доверительный интервал, то при малом числе измерений используют распределение Стьюдента, или t-распределение, которое обеспечивает возможность определения доверительных интервалов при ограниченном числе измерений. Границы доверительного интервала при этом определяются по формуле
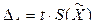 , (3.9)
, (3.9)
где t – коэффициент распределения Стьюдента, зависящий от задаваемой доверительной вероятности Рд и числа измерений n.
Коэффициент t обычно определяется по таблице (см. прилож. 3) или рассчитывается по сложной формуле, описывающей распределение Стьюдента.
Рассмотрим последовательность обработки экспериментальных данных прямых многократных измерений для следующих случаев:
результаты измерений являются исправленными, то есть из них исключены систематические погрешности;
неисключенные систематические погрешности настолько малы, что ими можно пренебречь;
результаты измерений являются равнорассеянными (равноточными) одинаково распределенными величинами (такие результаты получаются при выполнении измерений одним оператором с помощью одних и тех же средств измерений);
из результатов измерений исключены промахи и грубые погрешности;
число измерений не превосходит 15 (в этом случае признается и не проверяется нормальность распределения случайных погрешностей).
Последовательность обработки экспериментальных данных прямых многократных измерений:
1. Получение n результатов наблюдений.
2. Вычисление среднего арифметического 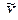 по формуле (3.6).
по формуле (3.6).
3. Вычисление оценки среднеквадратического отклонения результата измерения по формуле (3.8).
4. Принятие значения доверительной вероятности Рд (обычно Рд = 0,95).
5. Определение коэффициента t в зависимости от Рд и n по таблице распределения Стьюдента.
6. Определение доверительных границ 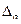 случайной погрешности по формуле (3.9).
случайной погрешности по формуле (3.9).
7. Запись результата измерений с использованием правил округления в виде А = 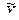 ±
± 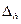 (Рд = …; n = …).
(Рд = …; n = …).
Обработка экспериментальных данных прямых однократных измерений
Прямые однократные измерения являются основным видом технических измерений и проводятся в том случае, когда ожидается пренебрежимо малая (по сравнению с инструментальной) случайная погрешность.
Результат прямого однократного измерения представляется в виде
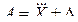 , (3.10)
, (3.10)
где 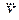 – значение физической величины, найденное по шкале измерительного прибора; D – абсолютная погрешность для найденного значения
– значение физической величины, найденное по шкале измерительного прибора; D – абсолютная погрешность для найденного значения 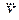 , определяемая классом точности L средства измерений.
, определяемая классом точности L средства измерений.
Класс точности средства измерений – обобщенная характеристика средств измерений, определяемая пределами допускаемых основной и дополнительной погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. В подавляющем большинстве случаев класс точности нормируется приведенной g или относительной d погрешности
|
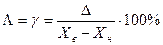 (3.11)
(3.11)
|
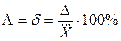 , (3.12)
, (3.12)
где X в и Xн – верхний и нижний пределы измерений используемого средства измерений.
Значение класса точности указывается на шкалах или корпусах измерительных устройств. Если число, определяющее класс точности, заключено в окружность (‚), то класс точности устройства следует определять по формуле (3.12), в противном случае – по формуле (3.11). 
Если класс точности на приборе представлен в виде 0,02/0,01, то он характеризуется пределами допускаемой основной относительной погрешности
|
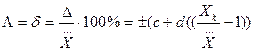 , (3.13)
, (3.13)
где Xk – конечное значение диапазона измерений или диапазона значений воспроизводимой многозначной мерой величины; с и d – постоянные числа (пример: с = 0,02; d = 0,01).
Таким образом, в каждом конкретном случае для определения значения D в выражении (3.10) необходимо выполнить вычисления по формулам, полученным из выражений (3.11) и (3.12, 3.13) соответственно:

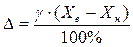 , (3.14)
, (3.14)
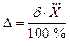 . (3.15)
. (3.15)
Описание лабораторного стенда
Лабораторный стенд (рис. 3.1) содержит:
щиток 1 электропитания стенда с автоматами «СЕТЬ» и «НАСОС»;
гидросистему, состоящую из бака с водой 2, задвижек З1 и З4, насоса 3;
многофункциональный цифровой ваттметр (на рис. 3.1 не показан) класса точности 0,1, показания которого отображаются на экране ноутбука;
датчик давления Р1.
Стенд подключается к электрической сети с помощью вилки 4.
Порядок выполнения работы:
1. C помощью вилки 4 подключить стенд к электрической сети.
2. Автомат «СЕТЬ» щитка 1 электропитания стенда установить в положение «Вкл.».
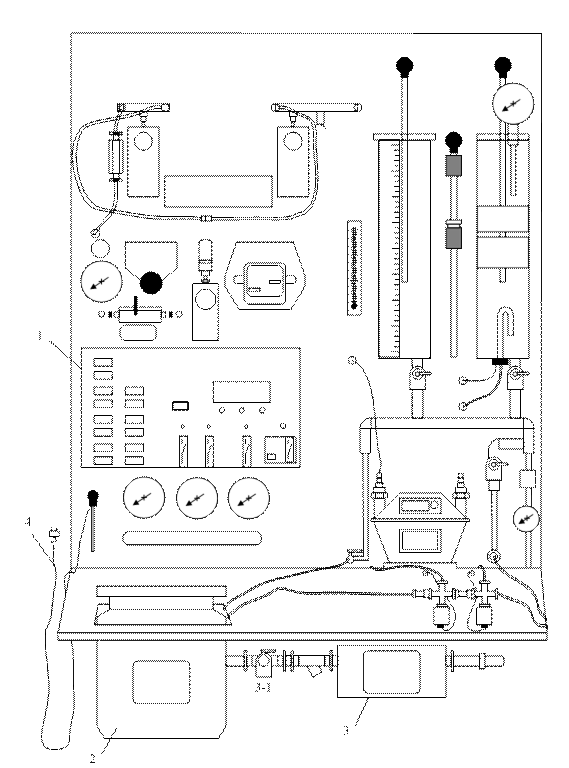
Рис. 3.1. Схема лабораторного стенда
3. Заполнить гидросистему водой: открыть задвижки З1 и З4 и включить автомат «НАСОС».
4. Подключить ноутбук к стенду. Запустить на ноутбуке программный комплекс E-LAB, ярлык которого находится на рабочем столе.
5. В окне программы выбрать при помощи мыши «Лабораторная работа № 14». Программа начнет считывание показаний много-функционального цифрового ваттметра и значений давления насоса 3.
6. Дождаться, пока давление насоса перестанет изменяться.
7. Выполнить многократные прямые измерения электрических пара-метров насоса, считывая показания цифрового ваттметра с экрана ноутбука через каждые 15 с. Выполнить 15 отсчетов, а результаты измерений записать в табл. 3.1. Таблицы для обработки многократных измерений напряжения, силы тока и мощности идентичны.
Таблица 3.1
Обработка экспериментальных данных
прямых многократных измерений
| № п/п | Результаты отдельных измерений | Значения оценок | Коэффициент, t | Довери-тельный интервал,
| Результат | |
 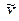
| S( 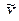 ) )
| |||||
8. Выполнить однократное измерение электрических параметров насоса. Результаты записать в табл. 3.2. Таблицы для обработки однократных измерений напряжения, силы тока и мощности идентичны.
Таблица 3.2
Обработка экспериментальных данных
прямых однократных измерений
Показания прибора,
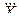
| Класс точности, L | Абсолютная погрешность, DХ | Результат, Х |
9. Отключить автоматы «НАСОС» и «СЕТЬ».
10. Вилку 4 отключить от электрической сети.
11. Обработать результаты многократных измерений. Результаты вы-числений занести в табл. 3.1.
12. Обработать результаты однократного измерения. Результаты вычислений занести в табл. 3.2.
13. В выводе пояснить, многократные или однократные измерения целесообразнее проводить в данной работе.
Вопросы для самоконтроля:
1. С помощью какого закона распределения описана случайная величина в данной лабораторной работе?
2. Назвать характеристики нормального закона распределения и дать им определения.
3. Записать формулы, по которым определяются характеристики нормального закона распределения.
4. Дать определение понятиям «доверительный интервал», «доверительная вероятность».
5. Как определить границы доверительного интервала в данной лабораторной работе?
6. Как определить коэффициент t?
7. Дать определение понятию «класс точности».
8. Как нормируется класс точности?
9. Как обозначается класс точности средств измерений?
10. Дать определение термину «диффузионность». Как она определяется?
11. Какая величина определяется как прямая в данной лабораторной работе? Привести пример прямого измерения.
12. Дать определение многократным и однократным измерениям.
13. Как определяется абсолютная погрешность при однократном измерении?
14. Дать определение случайным и систематическим погрешностям.
15. Дать определение понятиям «промах» и «грубая погрешность».
16. Назвать причины возникновения грубой погрешности.
17. Назвать правила округления результатов измерений и погреш-ностей измерений.
18. Какие результаты называются исправленными?
19. Что в себя включает методика выполнения измерений?
20. Пояснить метод непосредственной оценки измерения.
Лабораторная работа № 5
Выполнение и обработка экспериментальных данных
косвенных измерений
Цель работы: изучение методик выполнения и обработки экспериментальных данных косвенных многократных и однократных измерений.
Задание:
1. Изучить теоретические материалы к лабораторной работе.
2. Выполнить многократные косвенные измерения.
3. Выполнить однократные косвенные измерения.
4. Обработать полученные экспериментальные данные.
5. Составить расчет по лабораторной работе.
Теоретические основы работы
Обработка экспериментальных данных косвенных многократных измерений
Как уже отмечалось, косвенным называется измерение, при котором значение физической величины находят на основании известной зависимости между этой величиной и величинами, найденными в результате прямых измерений. Причем часть величин может определяться путем многократных измерений, а часть – однократными измерениями.
При косвенных измерениях искомая величина Y определяется зависимостью
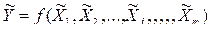 , (3.16)
, (3.16)
где 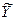 – функция случайных величин (аргументов), полученная после выполнения вычислительных операций со средними арифметическими значениями
– функция случайных величин (аргументов), полученная после выполнения вычислительных операций со средними арифметическими значениями 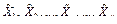 аргументов в соответствии с этой функцией.
аргументов в соответствии с этой функцией.
Средние арифметические величины аргументов определяются по формуле
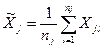 , (3.17)
, (3.17)
где nj – число измерений величины-аргумента Xj; Xjl – значение величины Xj, полученное при выполнении l-го измерения.
Оценка среднеквадратического отклонения результата косвенного измерения определяется по формуле
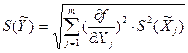 , (3.18)
, (3.18)
где S( 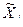 ) – оценка среднеквадратического отклонения результата измерений j-го аргумента, определяемого по формуле
) – оценка среднеквадратического отклонения результата измерений j-го аргумента, определяемого по формуле
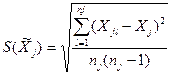 . (3.19)
. (3.19)
Например, для случая, когда при косвенном измерении используется функциональная зависимость:
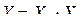 , (3.20)
, (3.20)
тогда оценка среднеквадратического отклонения результата косвенного измерения определяется по формуле
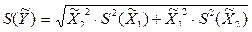 . (3.21)
. (3.21)
Частные производные в формуле (3.18) принято называть коэффициентами влияния. Они вычисляются при значениях переменных, равных 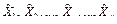 .
.
При обработке экспериментальных данных многократных косвенных измерений следует определять так называемую интервальную оценку погрешности результата косвенного измерения. Для случая, когда результаты, полученные в процессе прямых измерений величин-аргументов, имеют нормальный закон распределения (при числе измерений 5–15 этот факт просто принимается), используется распределение Стьюдента (t-раcпределение). Интервальная оценка определяется доверительной границей случайной погрешности результата косвенного измерения и вычисляется по формуле
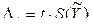 , (3.22)
, (3.22)
где t – коэффициент распределения Стьюдента.
Значение t определяется по таблице (см. прилож. 3) в зависимости от принятого или заданного значения доверительной вероятности Рд (обычно Рд = 0,95) и найденного расчетным путем значения эффективного числа степеней свободы Кэфф, которое находят по формуле
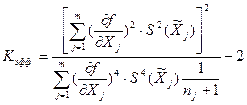 . (3.23)
. (3.23)
В случае, когда коэффициенты влияния 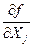 и число измерений nj для всех величин одинаковы, а также близки по модулям значения оценок среднеквадратических отклонений результатов измерений S(
и число измерений nj для всех величин одинаковы, а также близки по модулям значения оценок среднеквадратических отклонений результатов измерений S( 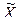 ), эффек-тивное число степеней свободы Кэфф можно вычислить по формуле
), эффек-тивное число степеней свободы Кэфф можно вычислить по формуле
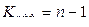 . (3.24)
. (3.24)
Последовательность обработки экспериментальных данных косвенных многократных измерений при соблюдении условий для прямых многократных измерений следующая:
1. Получение результатов измерений величин X1, X2, ..., Xj, ..., Xm.
2. Вычисление средних арифметических 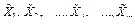 по формуле (3.17).
по формуле (3.17).
3. Вычисление значения 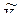 по формуле (3.16).
по формуле (3.16).
4. Вычисление оценок среднеквадратических отклонений резуль-татов измерений величин X1, X2, ..., Xj, ..., Xm по формуле (3.19).
5. Вычисление оценки среднеквадратического отклонения результата измерения величины Y по формуле (3.18).
6. Вычисление числа степени свободы Кэфф по формуле (3.23) или (3.24).
7. Принятие значения доверительной вероятности Рд (обычно Рд = 0,95).
8. Определение коэффициента t в зависимости от Рд и Кэфф по таблице распределения Стьюдента.
9. Определение доверительных границ 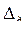 случайной погрешности по формуле (3.22).
случайной погрешности по формуле (3.22).
10. Запись результата измерений с использованием правил округления в виде 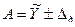 (Рд = …; Кэфф = …; n1 = …; n2 = …; …; nj = ...).
(Рд = …; Кэфф = …; n1 = …; n2 = …; …; nj = ...).
Обработка экспериментальных данных косвенных однократных измерений
Однократные косвенные измерения проводятся при условиях, когда всеми погрешностями, кроме погрешностей средств измерений, можно пренебречь. Оценка значения измеряемой величины при однократных косвенных измерениях находится из выражения
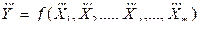 , (3.25)
, (3.25)
где 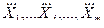 – значения физических величин-аргументов, найденные по шкалам соответствующих измерительных приборов.
– значения физических величин-аргументов, найденные по шкалам соответствующих измерительных приборов.
Результаты измерений записываются в виде
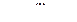 , (3.26)
, (3.26)
где D – оценка погрешностей косвенных однократных измерений.
При определении оценки погрешности косвенных однократных измерений считают, что погрешности измерений величин-аргументов являются случайными, имеющими равномерный закон распределения. На этом основании для определения D используют формулу (5.6), в которой вместо значения S( 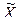 ) подставляют абсолютные погрешности измерений D(
) подставляют абсолютные погрешности измерений D( 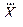 ) величин-аргументов.
) величин-аргументов.
Для случая, когда при косвенных измерениях используются функции вида (3.20), погрешность косвенных однократных измерений определяется из выражения
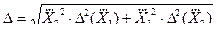 . (3.27)
. (3.27)
Для определения значений D( 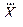 ) необходимо использовать информацию о классах точности применяемых средств измерений.
) необходимо использовать информацию о классах точности применяемых средств измерений.
В подавляющем большинстве случаев класс точности нормируется приведенной g или относительной d погрешностью:
|
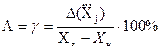 , (3.28)
, (3.28)
|
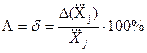 , (3.29)
, (3.29)
где Xв и Xн – верхний и нижний пределы измерений используемого средства измерений.
Значение класса точности указывается на шкалах или корпусах измерительных устройств. Если число, определяющее класс точности, заключено в окружность (‚), то класс точности устройства следует определять по формуле (3.28), в противном случае – по формуле (3.29).
Таким образом, в каждом конкретном случае для определения значений D( 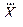 ) необходимо выполнять вычисления по формулам, полученным из выражений (3.28) и (3.29):
) необходимо выполнять вычисления по формулам, полученным из выражений (3.28) и (3.29):

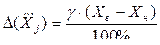 , (3.30)
, (3.30)
|
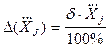 . (3.31)
. (3.31)
Описание лабораторного стенда
Лабораторная работа выполняется при помощи анемометра (рис. 3.2). Анемометр состоит из зонда 1, дисплея 2 и панели управления 3. На панели управления располагаются кнопки. Класс точности анемометра 0,5.
Порядок выполнения работы
Сущность экспериментов в данной лабораторной работе сводится к выполнению многократных и однократных измерений объемного расхода потока воздуха.
В данных косвенных измерениях используется функциональная зависимость между объемным расходом Q, площадью поперечного сечения F воздуховода и скоростью 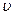 воздуха в сечении:
воздуха в сечении: 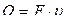 .
.
1. С помощью кнопки  , расположенной на панели управления 3, включить анемометр. Откроется окно измерений на дисплее 2.
, расположенной на панели управления 3, включить анемометр. Откроется окно измерений на дисплее 2.
 2. Поднести анемометр к вентилятору, вы-тяжному шкафу или форточке. Установить зонд 1 в необходимой позиции.
2. Поднести анемометр к вентилятору, вы-тяжному шкафу или форточке. Установить зонд 1 в необходимой позиции.
3. Дождаться момента времени, когда пока-зания прибора практически перестанут изме-няться.
4. Выполнить многократные прямые изме-рения скорости потока воздуха, считывая по-казания анемометра с дисплея через каждые 15 с. Выполнить 15 отсчетов, а результаты измерений записать в табл. 3.3.
5. С помощью кнопки  , расположенной на панели управления 3, выключить анемометр, удерживая несколько секунд кнопку.
, расположенной на панели управления 3, выключить анемометр, удерживая несколько секунд кнопку.
6. Повторно включить анемометр.
7. Выполнить однократные прямые изме-рения скорости потока воздуха, считав показания с дисплея анемометра. Результаты измерений записать в табл. 3.4.
|
 .
.
9. Рассчитать площадь поперечного сечения воздуховода.
10. Обработать результаты многократных и однократных измерений. Результаты вычислений занести в табл. 3.3 и 3.4.
Таблица 3.3
Обработка экспериментальных данных косвенных многократных измерений объемного расхода воды
| № п/п | Резуль-таты отдель-ных наб-людений,
| Оценки | Коэффициент Стьюдента, t | Доверительный интервал, Δ, м3/ч | Результат Q, м3/ч | ||||
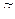 , м/с , м/с
| 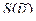
| F, м2 | Q, м3/ч | S(Q) | |||||
11. В выводе пояснить, многократные или однократные измерения целесообразнее проводить в данной работе.
При обработке экспериментальных данных по формулам принять X1 = 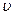 , X2 = F.
, X2 = F.
Таблица 3.4
Обработка экспериментальных данных
косвенных однократных измерений объемного расхода воды
| Показа-ния прибора,
| Площадь попереч-ного сечения воз-духовода, F, м2 | Оценки | Результат, Q, м3/ч | |||
| Q, м3/ч | 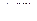 , м/с , м/с
| 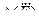 ,
м2 ,
м2
| 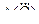 , м3/ч , м3/ч
| |||
Вопросы для самоконтроля:
1. Какая величина определяется косвенно, а какая прямо в данной лабораторной работе? Привести пример косвенного измерения.
2. С помощью какого закона распределения описана случайная величина многократных косвенных наблюдений?
3. Назвать характеристики нормального закона распределения и дать им определения.
4. По какой формуле определяется среднеквадратическое отклонение результата косвенного измерения?
5. Как определяются коэффициенты влияния?
6. Как рассчитать число степеней свободы?
7. Как записывается результат косвенного многократного измерения?
8. С помощью какого закона распределения описана случайная величина однократных косвенных наблюдений?
9. Как определяется коэффициент t?
10. Дать определение понятия «класс точности».
11. Как нормируется класс точности?
12. Как определить абсолютную погрешность косвенного одно-кратного измерения в данной лабораторной работе?
13. Определить класс точности вольтметра, если абсолютная погрешность измерения равна 0,05 мВ, верхнее значение диапазона измерения – 50 мВ.
14. Если класс точности на приборе изображен в виде 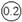 , как определить абсолютную погрешность прибора?
, как определить абсолютную погрешность прибора?
15. Дать определение терминам «многократные измерения» и «однократные измерения».
16. Назвать причины возникновения случайных погрешностей.
17. При каких условиях можно воспользоваться формулой Кэфф = n – 1 для определения числа степеней свободы?
18. Перечислить измерения по виду.
19. Назвать последовательность обработки экспериментальных данных косвенных многократных измерений.
20. Записать выражение для нахождения оценки средне-квадратического отклонения результата косвенного измерения сопротивления, вычисленного по формуле R = U/I.
Лабораторная работа № 6
Выполнение и обработка экспериментальных данных
совместных измерений
Цель работы: изучение методики выполнения и обработки экспериментальных данных совместных измерений.
Задание:
1. Изучить теоретические материалы к лабораторной работе.
2. Выполнить совместные измерения.
3. Обработать полученные экспериментальные данные.
4. Составить отчет по лабораторной работе.
Теоретические основы работы:
Совместные измерения представляют собой производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними.
Этот вид измерений находит широкое применение в научных, технических и метрологических измерениях.
Совместные измерения применяются в метрологической практике при экспериментальном определении градуировочных характеристик средств измерений, в том числе различных преобразователей.
Определение градуировочной характеристики средства измерения называется градуировкой средства измерения.
Градуировочная характеристика средства измерения представляет собой зависимость между значениями величин на входе и выходе средств измерений. Она может быть представлена в виде таблицы, графика или формулы (то есть в аналитическом виде).
Наиболее универсальной формой градуировочной характеристики является ее представление в виде формулы, которую удобно использовать с помощью ЭВМ.
В качестве примера рассмотрим совместные измерения, целью которых является определение статической характеристики термо-электрического измерительного преобразователя (ТЭП). Принцип действия ТЭП основан на термоэлектрическом эффекте, в соответствии с которым при нагревании спая из двух разнородных проводников на свободных концах этих проводников возникает ЭДС.
Статическую характеристику ТЭП можно описать выражением

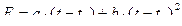 , (3.32)
, (3.32)
где а и b – неодноименные (имеющие различные размерности) коэффициенты; t и t0 – текущая и начальная температуры спая ТЭП.
Целью совместных измерений в данном случае является определение значений коэффициентов а и b.
|
|
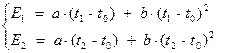 (3.33)
(3.33)
|
|
|
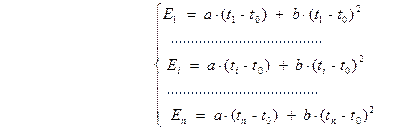 (3.34)
(3.34)
где Ei и En – значения сигнала ТЭП в i-м и n-м опытах; ti и tn – значения температуры в i-м и n-м опытах.
Надежным и научно обоснованным способом определения коэффициентов экспериментальных зависимостей является метод наименьших квадратов. Суть его заключается в подборе таких значений коэффициентов, при которых сумма квадратов отклонений, измеренных в опытах значений от рассчитанных, была бы минимальной. Данный метод позволяет не только найти коэффициенты функциональной зависимости, но и провести оценку погрешностей найденных коэффициентов. Так как метод наименьших квадратов требует выполнения большого объема вычислений и обычно реализуется с использованием ЭВМ, то воспользуемся более простым, но менее точным методом, который называется методом средних.
В соответствии с методом средних полученные уравнения делят на группы, число которых должно быть равно числу искомых величин. Число уравнений в группах должно быть примерно одинаковым. Уравнения в сформированных группах складывают, усредняют, а затем решают полученную систему уравнений.
Для рассматриваемого в данной лабораторной работе случая определения статической характеристики ТЭП необходимо разделить уравнения системы (3.34) на две группы, содержащие m и n–m уравнений:
|
|
|
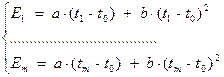 (3.35)
(3.35)
|
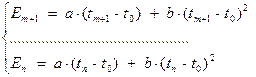 (3.36)
(3.36)
После сложения уравнений в системах (3.33) и (3.34) и их усреднения можно получить следующую систему уравнений:
|
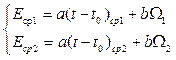 , (3.37)
, (3.37)
где 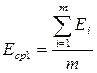 ;
; 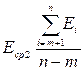 ;
; 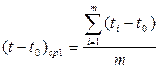 ;
; 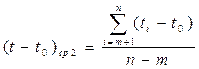 ;
; 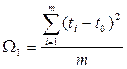 ;
; 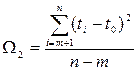 .
.
Из решения системы уравнений (3.37) находят значения искомых коэффициентов a и b статической характеристики ТЭП.
Описание лабораторного стенда
Лабораторный стенд (рис. 3.3) содержит:
щиток 1 электропитания стенда с автоматами;
калибратор «2500С», состоящий из ПИД регулятора 2, нагревателя 3, оснащенного полостями для установки датчиков температуры, и пульта управления 4 с кнопкой «СЕТЬ» и тумблером;
двухканальный измеритель МИТ 2.05М 5 и панель 6 для подключения датчиков к 1-му и 2-му каналам измерителя;
ноутбук 7 и соединительный шнур 8.
При помощи термометра сопротивления типа ТС-Pt100 9 измеряется температура калибратора. Для снятия статической характеристики используется термопара типа ТП-L 10.
Стенд подключается к электрической сети с помощью вилки 11.
Порядок выполнения работы
1. C помощью вилки 11 подключить стенд к электрической сети.
2. Автоматы щитка 1 электропитания стенда установить в положение «Вкл.».
3. Установить термометр сопротивления 9 в одну из полостей нагревателя 3 калибратора и подключить его ко входу «1» измерителя 5, соблюдая цвета вилок и гнезд.
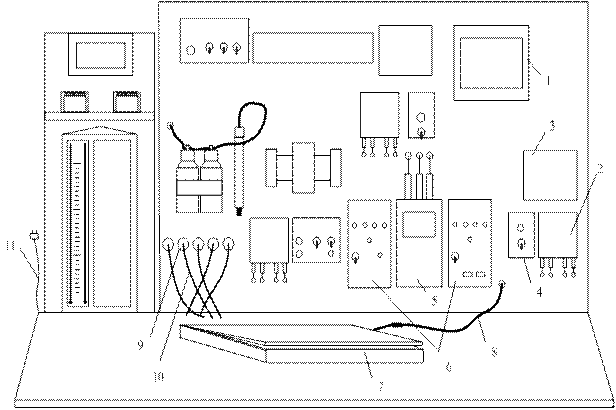
Рис. 3.3. Схема лабораторного стенда
4. Установить термопару 10 во вторую полость нагревателя 3 калибратора и подключить его ко входу «2» измерителя 5, соблюдая цвета вилок и гнезд.
5. Подключить ноутбук 7 к стенду при помощи шнура 8 и двух USB-кабелей и включить его.
6. Включить питание ПИД регулятора калибратора кнопкой «СЕТЬ» на пульте управления 4 и установить на регуляторе 2 при помощи кнопок значение уставки для калибратора «2500С», равное 200 0С. Считать начальное значение температуры с дисплея ПИД регулятора 2 и записать его в табл. 3.5.
7. Включить питание измерителя 5, удерживая 1–2 секунды кнопку включения на его панели.
8. Установить режимы измерителя 5. Для этого:
8.1. Запустить на ноутбуке 7 программу «МИТ 2.05.exe», ярлык которой находится на «Рабочем столе». Если программа не обнаружит подключенный измеритель, нажать значок «Обновить список доступных приборов».
8.2. Открыть «Настройки» и во вкладке «Каналы» настроить оба канала измерителя 5 в соответствии с подключенными датчиками и измеряемыми величинами.
Канал 1:
состояние – «Вкл.»;
тип измерения – ТС;
НСХ – Pt100.
Канал 2:
состояние – «Вкл.»;
тип измерения – мВ.
8.3. Передать эти настройки в измеритель 5 при помощи кнопки  и закрыть окно.
и закрыть окно.
9. Включить ПИД регулятор 2 при помощи тумблера на пульте управления 6, начав тем самым разогрев.
10. Включить мышкой режим «Считывание»: программа начнет считывание результатов измерений температуры и термоЭДС и вывод графиков на экран.
11. Дождаться выхода калибратора на заданную температуру. Отключить его питание тумблером на пульте управления 6.
12. Сохранить полученные данные в виде таблицы Microsoft Excel (рис. 3.4).
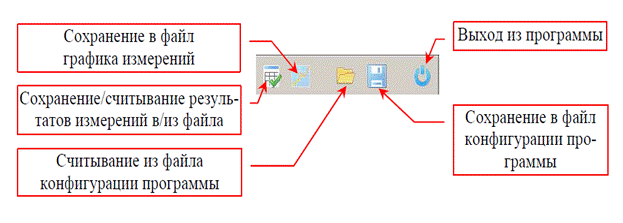
Рис. 3.4. Способы сохранения данных
13. Заполнить табл. 3.5 при помощи полученных графиков. Записать показания температуры и термоЭДС через каждые 30 секунд от начала эксперимента.
Таблица 3.5
Обработка экспериментальных данных совместных измерений
| № п/п | Значение темпе-ратуры, t, 0С | Значение термоЭДС, Е, мВ | Начальная темпера-тура, t0, 0С | Коэффициенты | Ерасч, мВ | DЕ, мВ | |
| а, (1/0С) | b, (1/0С)2 | ||||||
14. Отключить питание калибратора кнопкой «СЕТЬ» на пульте управления 6.
15. Установить тумблеры на щитке 1 в положение «Выкл.», а вилку 11 отключить от электрической сети.
16. Выключить ноутбук, отсоединив шнур 8 и два USB-кабеля.
17. Обработать результаты совместных измерений по методике, описанной выше, вручную или при помощи программы Microsoft Excel.
18. Определить значения коэффициентов а и b.
19. По модели сигнала ТЭП рассчитать значения сигнала Ерасч для всех экспериментальных значений температуры.
20. Определить абсолютную погрешность измерения ΔЕ для всех значений температуры. Результаты занести в табл. 3.5.
21. В выводе записать математическую модель сигнала ТЭП, используя коэффициенты а и b в виде выражения (3.30).
Вопросы для самоконтроля:
1. Дать определение понятию «совместные измерения». Какие величины определяются совместно?
2. Чем отличаются совместные измерения от совокупных?
3. Назвать принцип действия ТЭП.
4. Каким уравнением описывается статическая характеристика ТЭП?
5. Дать определение понятию «статическая характеристика».
6. С помощью какого метода находятся коэффициенты а и b ?
7. Пояснить метод средних.
8. Записать модель сигнала ТЭП, используя коэффициенты а и b.
9. Дать определение понятию «измерительный преобразователь». Привести пример.
10. Перечислить приборы и преобразователи на стенде.
11. Как определяется абсолютная погрешность?
12. Перечислить классификацию измерений по способу получения результата.
13. Дать определения одноименным и неодноименным величинам.
14. Чем характеризуется точность измерения?
15. Дать определения терминам «точность», «достоверность», «правильность», «сходимость», «вопроизводимость».
16. Пояснить метод непосредственной оценки.
17. Пояснить метод сравнения с мерой.
18. Дать определение понятия «измерительный эксперимент».
19. Что в себя включает методика измерений?
20. Перечислить НТД, регламентирующую методику измерений.
Приложения
Приложение 1
Дата: 2019-11-01, просмотров: 470.