Измерительного преобразователя
| Значение входного сигнала, X, 0С | Номи-нальное значе-ние выход-ного сигна-ла, Yн, Ом | Значение выходного сигнала, Yр = fр(X), Ом | Абсолютная погрешность, D, Ом | Вари-ация, W, Ом | |||
| Пря-мой ход | Обрат-ный Ход | Прямой ход | Обрат- ный ход | Пря-мой ход | Обрат- ный ход | ||
| 0 | 0 | ||||||
| 50 | 50 | ||||||
| … | … | ||||||
| 250 | 250 | ||||||
23. Из таблицы (см. прилож. 1) номинальной статической характеристики ТС-50П определить номинальное значение сопротивления и занести в табл. 2.2.
24. Установить тумблеры на щитке 1 в положение «Выкл.», а вилку 14 отключить от электрической сети.
25. Выключить ноутбук, отсоединив шнур 11 и два USB-кабеля.
26. Построить график реальной функции преобразования, нанеся предварительно на график номинальную функцию преобразования.
27. По результатам исследований приписать измерительному преобразователю абсолютную погрешность и вариацию. Записать полученные результаты в вывод.
Вопросы для самоконтроля:
1. Дать определение термину «статическая характеристика». Каким уравнением она описывается?
2. Как называется статическая характеристика для измерительных приборов и измерительных преобразователей?
3. Дать определение термину «градуировочная характеристика».
4. Изобразить на графике виды статической характеристики.
5. Чем отличается диапазон показаний от диапазона измерений?
6. Что такое чувствительность и как она определяется?
7. Что такое коэффициент преобразования и как он определяется?
8. Как определить цену деления?
9. Дать определение термину «порог чувствительности».
10. Охарактеризовать следующие виды погрешностей: аддитивная, мультипликативная, линейности и гистерезиса. Изобразить их графическим способом и назвать причины возникновения.
11. Дать определения терминам «шум», «фон», «дрейф нуля».
12. Дать определения терминам «номинальная» и «реальная функция преобразования».
13. Дать определение терминам «размах» и «вариация».
14. Как по графику определить абсолютную погрешность и вариацию?
15. Для какого устройства определялась статистическая характеристика в данной лабораторной работе?
16. Как определяется абсолютная погрешность измерения и вариация?
17. Дать определение терминам «измерительный прибор» и «преобразователь».
18. Нарисовать структурные схемы измерительных приборов.
19. Нарисовать структурные схемы измерительных преобразователей.
20. Перечислить основные составные части измерительных устройств.
Лабораторная работа № 2
Определение динамической характеристики
измерительного устройства
Цель работы: изучение современных представлений о работе измерительного устройства в динамическом режиме и освоение методики экспериментального определения динамической характеристики измерительного устройства.
Задание:
1. Изучить теоретические материалы к лабораторной работе.
2. Экспериментальным путем определить кривую разгона измери-тельного преобразователя.
3. По кривой разгона определить передаточную функцию измери-тельного преобразователя.
4. Составить отчет по лабораторной работе.
Теоретические основы работы
Динамическая характеристика измерительного устройства – это зависимость выходного сигнала от входного в динамическом режиме работы. Режим работы измерительного устройства, при котором значения выходного и входного сигналов изменяются во времени, называют динамическим (нестационарным, или неравновесным) [6].
Практически все измерительные устройства имеют в своем составе инерционные элементы: подвижные механические узлы, электрические и пневматические емкости, индуктивности, элементы, обладающие тепловой инерцией, и т. п. Наличие инерционных элементов приводит к тому, что в динамическом режиме мгновенное значение выходного сигнала измерительного устройства зависит не только от мгновенного значения входного сигнала, но и от любых изменений этого сигнала. Это определяет инерционность всего измерительного устройства. Указанные инерционные свойства измерительных устройств определяют динамической характеристикой.
Динамическую характеристику измерительного устройства принято описывать дифференциальным уравнением, передаточной или комплексной частотной функциями.
В подавляющем большинстве случаев динамическая характеристика измерительных устройств в линейной части статической характеристики (для измерительных устройств с линейной статической характеристикой во всем диапазоне преобразований) может быть описана дифференциальным уравнением вида
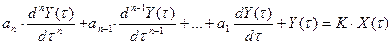, (2.9)
передаточной функцией
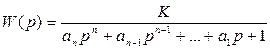(2.10)
либо
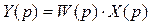, (2.11)
где Y(t) и X(t) – выходной и входной сигналы измерительного устройства как функции времени; n – число, определяющее порядок производной; Y(p) и X(p) – изображения выходной и входной величин, получаемые с помощью преобразований Лапласа комплексно-частотной функцией
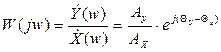, (2.12)
где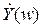 
и 
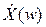– гармонические сигналы на комплексной плоскости; w – угловая частота; Ах и Ау – амплитуда гармонического сигнала на входе и выходе; θx и θy – начальная фаза на входе и выходе.
Передаточная функция и дифференциальное уравнение позволяют определять реакцию измерительного устройства на входные сигналы, изменяющиеся во времени по любому закону. Передаточную функцию измерительных устройств определяют обычно через переходную, или временную, характеристику, которая определяется как изменение во времени выходного сигнала Y(t) измерительного устройства при подаче на его вход скачкообразного сигнала, равного по значению единице входной величины. Если высота скачкообразного входного сигнала не равна единице, а имеет некоторое значение XА, то по переходной характеристике можно определить выходной сигнал, используя выражение
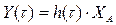. (2.13)
Для определения инерционных свойств измерительных устройств по переходным характеристикам обычно используют заимствованное из теории автоматического регулирования понятие динамического звена. Переходные характеристики и передаточные функции типовых динамических звеньев известны, что позволяет по форме переходной характеристики измерительного устройства отождествить его с каким-либо типовым динамическим звеном, а следовательно, определить форму передаточной функции испытываемого измерительного устройства. На рис. 2.11 и 2.12 показаны наиболее типичные для измерительных устройств формы переходных характеристик, то есть кривые переходных процессов или кривые разгона.
Для их получения в нулевой момент времени входной сигнал измерительного устройства скачком изменяется на XА от некоторого значения X1 до X2 (рис. 2.11а). По окончании переходного процесса выходной сигнал измерительного устройства изменяется на YА от значения Y1 до Y2 (рис. 2.11б).
Для определения коэффициента преобразования К измерительного устройства достаточно вычислить отношение
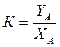. (2.14)
Переходный процесс, показанный на рис. 2.11б, соответствует типовому безынерционному (усилительному) звену. Данный процесс характерен для электронных измерительных устройств.
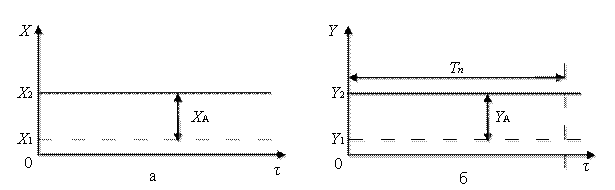Рис. 2.11. Переходный процесс безынерционного звена:
а – изменение входного сигнала измерительного устройства;
б – измение выходного сигнала
Переходные процессы, показанные на рис. 2.12а и 2.12б, соответствуют типовым звеньям: инерционному (апериодическому) первого порядка и колебательному.
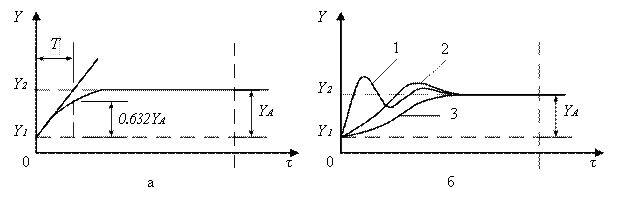Рис. 2.12. Переходные процессы:
а – инерционное звено первого порядка;
б – колебательное звено
Колебательное динамическое звено, а следовательно, и измерительное устройство, в котором имеет место переходный процесс (см. рис. 2.12б), можно рассматривать как соединение двух инерционных звеньев с постоянными времени Т1 и Т2. При этом в зависимости от соотношения Т1 и Т2 переходный процесс будет различен. Если (Т1/Т2) < 2, то график процесса имеет форму кривых 1 и 2, а при (Т1/Т2) ³ 2 – форму кривой 3 (см. рис. 2.12б). Эти процессы характерны для большого числа измерительных устройств.
Переходные процессы, показанные на рис. 2.13а и 2.13б, характерны для случаев, когда дифференциальное уравнение, описывающее динамику измерительного устройства, имеет порядок более, чем второй. В этих случаях принято рассматривать измерительные устройства как совокупность нескольких соединенных последовательно типовых динамических звеньев.
Измерительное устройство с переходным процессом, показанным на рис. 2.13а, можно рассматривать как соединение звена чистого запаздывания со временем запаздывания tз и инерционного звена с постоянной времени Т.
Измерительное устройство с переходным процессом, показанным на рис. 2.13б, можно рассматривать как соединение звена чистого запаздывания и колебательного звена.
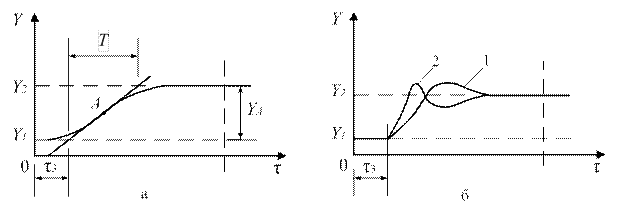Рис. 2.13. Переходные процессы: а – соединение звена
чистого запаздывания и инерционного звена с постоянной времени;
б – соединение звена чистого запаздывания и колебательного звена
Дифференциальные уравнения и передаточные функции рассмотренных наиболее типичных по инерционным свойствам измерительных устройств приведены в табл. 2.3.
Кривая (см. рис. 2.13а) представляет собой экспоненту, а величина Т (подкасательная) называется постоянной времени. Она определяет собой время, за которое выходной сигнал достиг бы нового установившегося значения, если бы изменялся с постоянной скоростью, равной скорости в момент скачкообразного изменения входного сигнала. Для графического определения значений Т достаточно провести касательную в точке перегиба А. Проведение касательной к кривой переходного процесса сопряжено с погрешностями, поэтому значение постоянной времени определяют как интервал времени, за который выходной сигнал изменяется на 0,632 от своего приращения YА (см. рис. 2.12а).
Время запаздывания – это время, в течение которого при подаче на вход возмущающего воздействия входная величина не изменяет своих значений (см. рис. 2.13а и 2.13б).
Для всех измерительных устройств важным является время установления выходного сигнала Тп (см. рис. 2.11б), которое также называют временем реакции. Оно представляет собой отрезок времени, необходимый для завершения переходного процесса при скачкообразном изменении входного сигнала.
Таблица 2.3
Типичные дифференциальные уравнения
и передаточные функции измерительных устройств
| Кривая переход-ного процесса | Дифференциальное уравнение | Передаточная функция |
| Рис. 2.11б |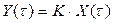 
| К |
| Рис. 2.12а |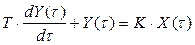 
| 
|
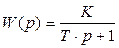
| Рис. 2.12б |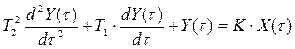 
| 
|
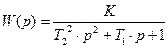
| Рис. 2.13а |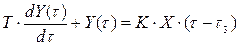 
| 
|
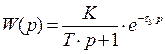
| Рис. 2.13б |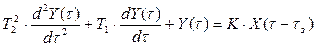 
| 
|
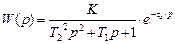
Так как в основном все рассмотренные переходные процессы (см. рис. 2.11–2.13) теоретически заканчиваются при бесконечном значении времени, то за время реакции Тп обычно принимают время, за которое выходной сигнал измерительного устройства, приближаясь к новому установившемуся значению, входит в некоторую зону, отличающуюся от этого значения на ±5 % от изменения выходного сигнала, соответствующего данному скачкообразному входному сигналу.
Значение времени реакции может быть приближенно определено через постоянную времени измерительного устройства из соотношения
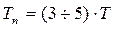. (2.15)
Описание лабораторного стенда
Лабораторный стенд (рис. 2.14) содержит:
щиток 1 электропитания стенда с автоматами «СЕТЬ», «НАСОС» и «НАГРЕВАТЕЛЬ»;
гидросистему, состоящую из бака с водой 2, задвижек З1, З4 и З6 и насоса 3;
емкость 4 с нагревателем 5;
термометр сопротивления ТС-50М 6.
Стенд подключается к электрической сети с помощью вилки 7.
Порядок выполнения работы
Сущность экспериментального исследования работы термометра сопротивления состоит в определении кривой разгона, которую получают путем скачкообразного изменения температуры термометра сопро-тивления, а именно путем размещения этого преобразователя последо-вательно в емкость с холодной, горячей и опять холодной водой. Это позволяет получить кривые разгона как при увеличении, так и при уменьшении измеряемого параметра.
1. C помощью вилки 7 подключить стенд к электрической сети.
2. Автомат «СЕТЬ» щитка 1 электропитания стенда установить в положение «Вкл.».
3. Заполнить гидросистему водой: открыть задвижки З1 и З4 и включить автомат «НАСОС».
4. Открыть задвижку З6 и наполнить емкость 4 таким образом, чтобы 50 % термометра сопротивления 6 было в воде. Закрыть задвижку З6.
5. Отключить автомат «НАСОС».
6. Подключить ноутбук к стенду. Запустить на ноутбуке программный комплекс E-LAB, ярлык которого находится на «Рабочем столе».
7. В окне программы выбрать при помощи мыши «Лабораторная работа № 3». Программа начнет считывание показаний.
8. Включить автомат «НАГРЕВАТЕЛЬ».
9. Наблюдать за движением графика. На графике при этом регистрируется кривая разгона.
10. Когда значение сигнала, регистрируемого на графике, достигнет установившегося значения, отключить автомат «НАГРЕВАТЕЛЬ» и слить воду, открыв задвижку З6. При этом на графике будет регистрироваться кривая разгона, соответствующая скачкообразному уменьшению значения измеряемой величины (для ускорения процесса налить в емкость 4 воды).
11. Дождаться установления постоянного значения сигнала, регис-трируемого компьютером.
12. Отключить автомат «СЕТЬ».
13. Вилку 7 отключить от электрической сети.
14. Определить значения сопротивлений для заданной температуры (см. прилож. 2).
15. Заполнить табл. 2.4, для этого записать значения температуры, соответсвующие каждым 10 с измерения до установления постоянного значения сигнала при охлаждении термометра сопротивления.
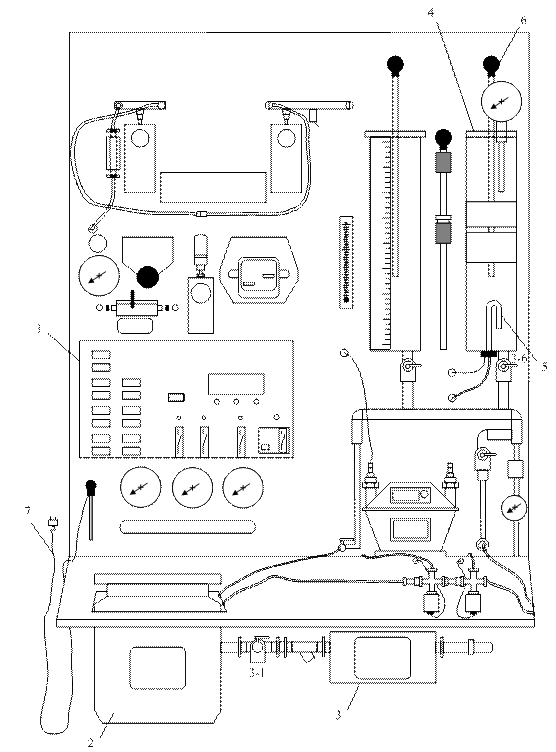
Рис. 2.14. Схема лабораторного стенда
Таблица 2.4
Результаты измерения
| № п/п | Время, Т, с | Температура, t, 0C |
| 1 | 0 | |
| 2 | 10 | |
| 3 | 20 | |
| 4 | 30 | |
| 5 | … |
Для снятия данных графика необходимо зажать клавишу Ctrl и при помощи клавиши → двигать ось вправо.
16. Построить кривые разгона для нагрева и охлаждения (по оси Х отложить время, с; по оси У – температуру, 0С).
17. По кривым разгона заполнить табл. 2.5.
18. Определить передаточные функции термометра сопротивления 6 для случаев скачкообразного изменения температуры. Для получения передаточных функций принять, что термометр сопротивления представ-ляет собой последовательное соединение звена чистого запаздывания и инерционного звена первого порядка. Результаты расчетов занести в табл. 2.5.
19. В выводе записать полученную передаточную функцию.
Таблица 2.5
Дата: 2019-11-01, просмотров: 272.
