Основой для раздела служит материал, собранный во время стажировки.

Задание на стажировку:

- выбрать параметр, контроль которого осуществляется СИ;

- произвести 50 измерений (выборка) и зафиксировать результаты.

В дипломной работе выполнить обработку прямых многократных равноточных измерений.

Порядок обработки результатов измерений:

а) произвести точечные оценки закона распределения результатов измерений;

б) определить закон распределения случайных величин;

в) определить доверительные границы погрешности результатов измерений и сравнить их с нормированными погрешностями.

Методика обработки результатов измерений.

Точечные оценки закона распределения результатов измерений:

а) определить среднее арифметическое значения измеряемой величины, 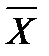, мм, по формуле

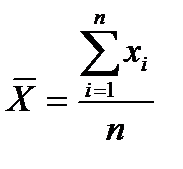,                                              (8.1)

где 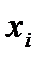 – значение измеряемой величины, мм;

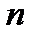 – число значений в выборке;

б) определить среднеквадратическое отклонение (СКО), σ, мм, по формуле

,                            (8.2)

где  – оценка СКО, равная значению СКО, мм;

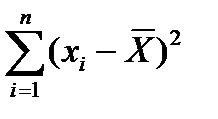 - сумма квадратов разницы между значением измеряемой величины и средним арифметическим значением, мм²;

Примечание – Удобно расчет суммы квадратов разницы представить в виде таблицы 3.

Таблица 3

В миллиметрах

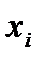
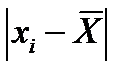
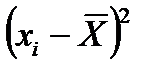
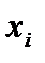
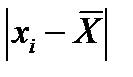
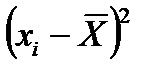
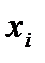
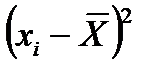
в) произвести оценку среднего арифметического отклонения, 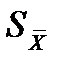, мм, по формуле

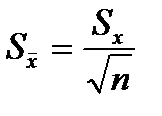;                                               (8.3)

г) осуществить проверку грубой погрешности с помощью критерия «Трёх сигм».

Критерий «Трех сигм»: практически все значения нормально распределённой случайной величины лежат в интервале .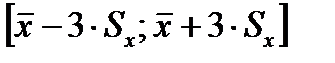

Проверить по крайним значениям выборки наличие грубой погрешности в выборе использую формулу:

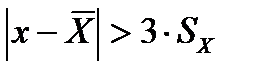.                                   (8.4)

Подставлять по очереди в формулу (8.4) наименьшее ( 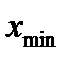) и наибольшее ( 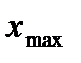) значение выборки, если неравенство соблюдается, то оцениваемые значения не являются грубой погрешностью, в противном случае являются грубой погрешностью и их необходимо исключить из выборки, а точечные оценки закона распределения результатов измерений производить заново без грубых погрешностей. Точечные оценки производят до тех пор, пока в выборке не останется грубой погрешности.

Закон распределения случайных величин:

а) преобразовать результаты контроля в выборку, упорядоченную в порядке возрастания;

б) определить количество интервалов, 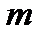, для построения полигона:

1) наибольшее значение, , определяем по формуле

;                                       (8.5)

2) наименьшее значение, 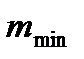, определяем по формуле

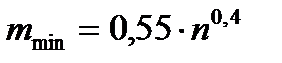;                                       (8.6)

Примечание - Количество интервалов определяют исходя из условия, что 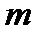, должно быть наименьшим нечетным целым числом между  и .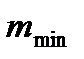

в) определить шаг гистограммы, 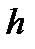, мм, по формуле

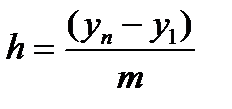,                                          (8.7)

где 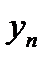 – последнее значение в выборке, мм;

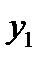 – первое значение в выборке, мм.

г) определить интервалов группирования 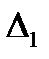, , 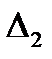 по формуле

,                             (8.8)

где при : ,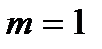

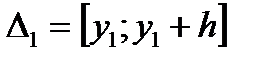при : ,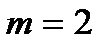

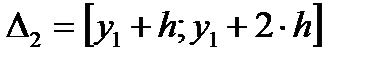при : ;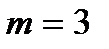

г) определить количество результатов измерений, , входящих в каждый интервал группирования, используя выборку, записать результаты для каждого интервала;

д) рассчитать значение вероятности для каждого интервала

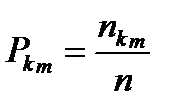;                                     (8.9)

е) построить гистограмму:

1) по оси 0х откладываем значения интервалов группирования 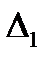, , , 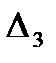…,  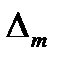в порядке возрастания номеров;

2) по оси 0 y отмечаем найденные значения вероятности

3) строим гистограмму, столбцы которой по высоте равны значению ;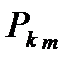

4) на оси 0х отмечаем верхнее и нижнее предельные отклонения для измеряемой величины;

5) соединяем середины вершин каждого столбца гистограммы и получаем полигон, который представляет собой ломанную кривую;

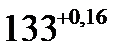Пример – Изображение гистограммы и полигона для контролируемого размера  мм (см. рисунок 1)

ж) сделать вывод по форме полигона и виду гистограммы.

Доверительные границы погрешности результатов измерений:

а) определить доверительные границы случайной погрешности, , мм, по формуле

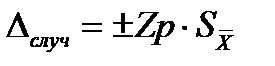 при 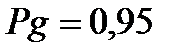,                          (8.10)

где 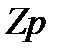 - квантильный множитель функции Лапласа, который определяется по справочным таблицам и зависит от значения ;

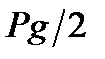б) определить систематическую погрешность, , мм: в качестве границы не исключённой систематической погрешности  принимаем одно деление шкалы используемого СИ, которое составляет 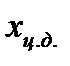 мм;

в) найти значение расчётной погрешности, 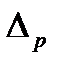, мм, по формуле

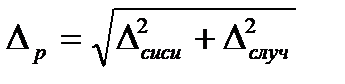;                                  (8.11)

г) записать результат измерения с учетом доверительных границ погрешности:

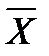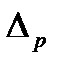±  мм, при ;

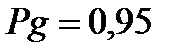д) определить нормируемую погрешность, 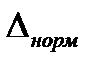, мм, по справочным таблицам для измеряемой величины;

е) сравнить значение расчетной и нормируемой погрешностей: ;

ж) сделать вывод.