Постоянная расчетная нагрузка:
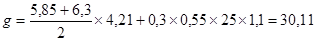 кН/м.
кН/м.
Временная расчетная нагрузка:
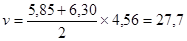 кН/м.
кН/м.
Полная нагрузка
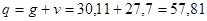 кН/м.
кН/м.
Определение изгибающих моментов и поперечных сил
Расчетный пролет крайнего пролета равен расстоянию от оси опорной площадки на стену до оси первой колонны
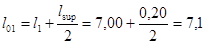 м.
м.
Расчетный средний пролет принимается равным расстоянию между осями колонн 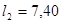 м. Для трехпролетной балки рассматриваются 5 схем загружения [рис. 3.2]. Расчеты по упругой схеме работы приведены в таблице 3.1.
м. Для трехпролетной балки рассматриваются 5 схем загружения [рис. 3.2]. Расчеты по упругой схеме работы приведены в таблице 3.1.
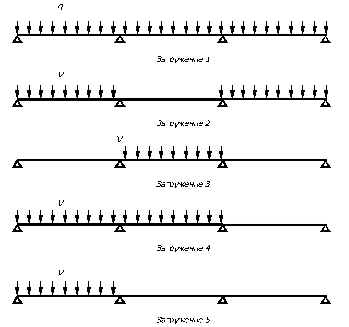
Рис. 3.2 - Схемы загружения ригеля
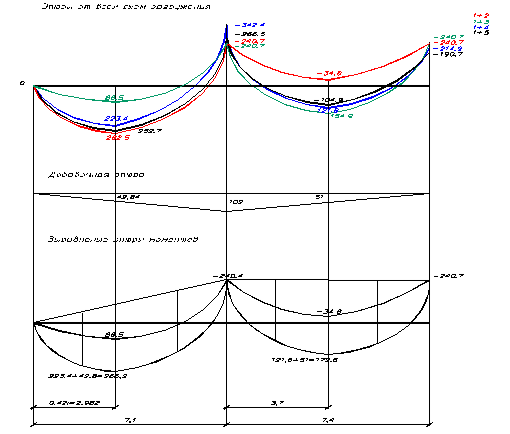
Рис 3.3 - Эпюры изгибающих моментов в сечениях ригеля
Для выравнивания опорных моментов по схеме (1 + 4) накладываем на полученную эпюру треугольную добавочную эпюру, с ординатой вершины равной 324,4 х 0,3= 102,4 ≈ 102 кНм. Изгибающий момент на опоре В станет равным
-342,4+102= -240,4 кНм. Тогда момент в первом пролете станет равным 223,4 + 42,84 =266,2 кНм. Так как эта величина больше максимального момента равного 262,5 кНм (1 + 2), то он является расчетным в первом пролете. На опоре С максимальный момент составляет -240,7 кНм (1+5). Для его выравнивания с моментом на опоре В накладываем вторую добавочную эпюру с ординатой вершины равной 102 кНм. Изгибающий момент на опоре В станет равным -342,4+102= -240,4 кНм. Во втором пролете изгибающий момент станет равным 121,6+51= 172,6 кНм, что больше 154,9 кНм (1 + 3), и он также является расчетным. Выровненная эпюра моментов приведена на рисунке 3.1 б).
Для расчета прочности наклонных сечений принимаются значения поперечных сил большее из двух расчетов: упругого и с учетом выравнивания моментов из-за пластических деформаций. Результаты упругого расчета приведены в таблице 3.1. Значения поперечных сил при учете выровненных моментов определяются по формулам для однопролетной балки :
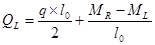 и
и 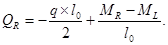
После подстановки значений ML и MR [рис. 14] получим:
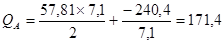 кН;
кН;
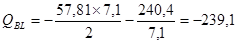 кН;
кН;
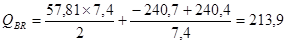 кН;
кН;
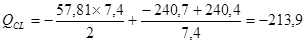 кН
кН
Результаты сведены в таблицу 3.2. Поперечные силы имеющие наибольшее значение являются расчетными.
Таблица 3.2 - Поперечные силы у опор балок
| Вид расчета | Поперечные силы на опорах | |||
| QA | QBL | QBR | QCL | |
| Упругий расчет (схемы) | (1 + 2) 174 | (1 + 4) -249,6 | (1 + 4) 230,9 | (1 + 4) -196,9 |
| С учетом пластических деформаций | 171,4 | -239,1 | 213,9 | -213,9 |
Подбор сечения продольной арматуры
Бетон класса В20 имеет характеристики: расчетное сопротивление при сжатии Rb = 11,5 МПа, то же при растяжении Rbt = 0,9 МПа, коэффициент условий работы бетона gb2 = 0,9 модуль упругости ЕB = 24000 МПа [3, табл.13, 15 и 18]. Арматура класса A-III имеет характеристики: расчетное сопротивление Rs = 365 МПа и модуль упругости Es = 200000 МПа. Размеры сечения ригеля 30´55 см.
Подбор сечения арматуры производим в расчетных сечениях ригеля.
Сечение в первом пролете
М = 266,2 кНм [рис. 3.3]; 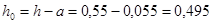 м;
м;
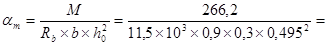 0,349,
0,349,
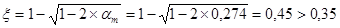
Необходимо изменить сечение: Примем h=65см.
Вычислим новый собственный вес балки и расчетную нагрузку на погонный метр балки
При h= 55 см Qb = b h γ = 0,3 x 0,55 x 25 = 4.125 кН/м,
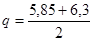 8,77+4.125·1,1= 57.82 кН/м.
8,77+4.125·1,1= 57.82 кН/м.
При h= 65 см Q*b = b h γ = 0,3 x 0,65 x 25 = 4.875 кН/м,
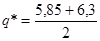 8,77+4.875·1,1= 58.64 кН/м.
8,77+4.875·1,1= 58.64 кН/м.
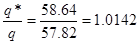
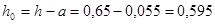 м;
м;
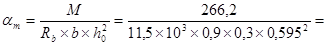 0,242
0,242
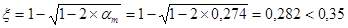
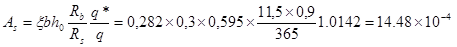 м2
м2
Принимаем 4Æ22A-III As = 15,2 см2 [1, прил. 4].
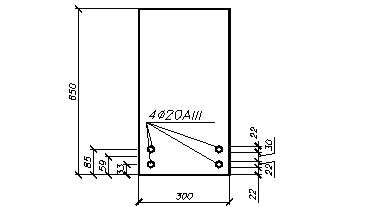
Рис. 3.4 – Сечение ригеля в первом пролете
Определим фактическую несущую способность балки в первом пролёте МU1, при полном количестве арматуры. Фактическая высота сжатой зоны:
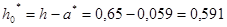 м;
м;
где а*= (у1 +у2)/2=(33+85)/2 = 59мм,
у1=22+22/2=33 мм, у2=22+22+30+22/2=85 мм [3, п.5.12];
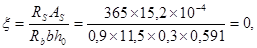 302<0.35,
302<0.35,
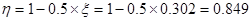
МU1= 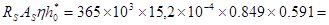 278.37кНм > 266,2 кНм.
278.37кНм > 266,2 кНм.
Необходимая несущая способность обеспечена.
Сечение во втором пролете
М = 172,6 кНм;
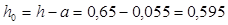 м; вычисляем:
м; вычисляем:
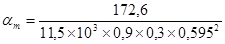 =0,157
=0,157
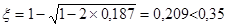 ,
,
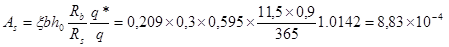 м2.
м2.
Принимаем 6Æ14A-II, c As =9.23 см2.
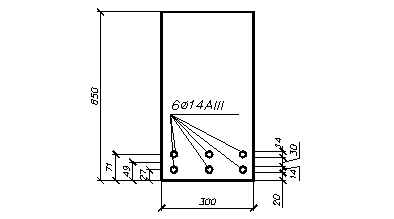
Рис. 3.5 – Сечение ригеля во втором пролете
Определим фактическую несущую способность балки во втором пролёте МU2, при полном количестве арматуры. Фактическая высота сжатой зоны:
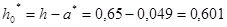 м;
м;
где а*=(27+71)/2 = 49мм,
у1=20+14/2=27 мм, у2=20+14+30+14/2=71 мм [3, п.5.12];
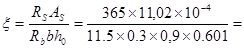 0,181
0,181
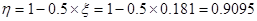 ,
,
МU2= 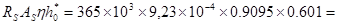 184.15кНм > 172,6 кНм.
184.15кНм > 172,6 кНм.
Необходимая несущая способность обеспечена.
3.5.3 Сечение на опоре В
М1 = 240,4 кНм; 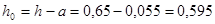 м.
м.
Определяем изгибающий момент у грани колонны со стороны второго пролета (QBL > QBR):
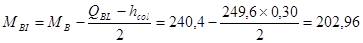 кНм.
кНм.
Вычисляем:
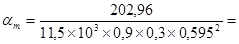 0,184,
0,184,
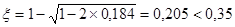 ,
,
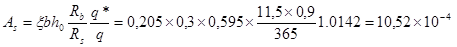 м2
м2
Принимаем 3Æ18A-III в верхней части, c As =7.63 см2, и 3Æ12 A-III,
c As =3.39см2 , общей площадью As = 11.02 см2
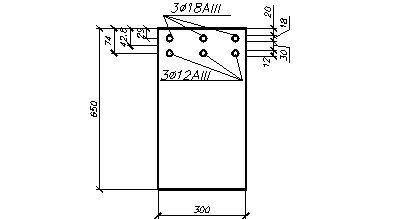
Рис. 3.7 – Сечение ригеля у опоры B
Определим фактическую несущую способность балки на опоре С МUС, при полном количестве арматуры. Фактическая высота сжатой зоны:
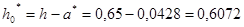 м;
м;
где а*= 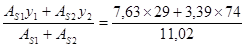 =42.8 см,
=42.8 см,
у1=20+18/2=29 см, у2=20+18+30+12/2=74 см [3, п.5.12];
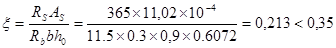 ,
,
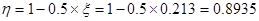 ,
,
МUС= 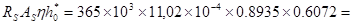 218.2кНм > 208,6 кНм.
218.2кНм > 208,6 кНм.
Необходимая несущая способность обеспечена.
Сечение на опоре С
М = 240,7 кНм; 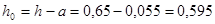 м;
м;
Определяем изгибающий момент у грани колонны со стороны второго пролета (QBL > QBR):
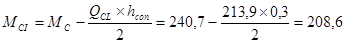 кНм.
кНм.
Вычисляем:
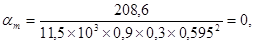 19
19
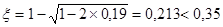
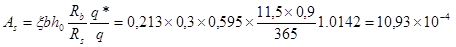 м2.
м2.
Принимаем 3Æ18A-III в верхней части, c As =7.63 см2, и 3Æ12 A-III,
c As =3.39см2 , общей площадью As = 11.02 см2

Рис. 3.7 – Сечение ригеля у опоры С
Определим фактическую несущую способность балки на опоре С МUС, при полном количестве арматуры. Фактическая высота сжатой зоны:
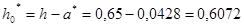 м;
м;
где а*= 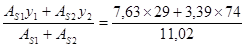 =42.8 см,
=42.8 см,
у1=20+18/2=29 см, у2=20+18+30+12/2=74 см [3, п.5.12];
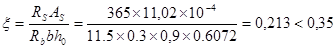 ,
,
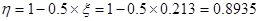 ,
,
МUС= 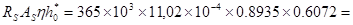 218.2кНм > 208,6 кНм.
218.2кНм > 208,6 кНм.
Необходимая несущая способность обеспечена.
Дата: 2019-11-01, просмотров: 369.