Данный многофакторный анализ занимает центральное место в моделировании. Многофакторные модели служат основным средством прогнозирования экономических результативных признаков, а также средство оценки роли каждого отдельного фактора в объяснении вариации результативных признаков.
Для многофакторного анализа и моделирования необходимо прежде всего необходимо соблюдения некоторых условий: достаточной численности совокупности (выборки), близости распределения ее по результативному и по всем факторным признакам к нормальному закону распределения, соблюдение гомоскедастичности.
Имеем исходные данные задачи.
| год | Всего безработных, Y | мужчин, Х1 | женщин, Х2 | Время, X3=t |
| 1995 | 6712 | 3616 | 3096 | 1 |
| 1996 | 6732 | 3662 | 3070 | 2 |
| 1997 | 8058 | 4371 | 3687 | 3 |
| 1998 | 8902 | 4792 | 4110 | 4 |
| 1999 | 9094 | 4801 | 4293 | 5 |
| 2000 | 6999 | 3781 | 3219 | 6 |
| 2001 | 6303 | 3411 | 2893 | 7 |
| 2002 | 6268 | 3385 | 2883 | 8 |
| 2003 | 5951 | 3148 | 2803 | 9 |
| 2004 | 6116 | 3076 | 3040 | 10 |
Теперь рассмотрим систему показателей тесноты - построим корреляционную матрицу.
|
| Y | X1 | X2 | X3 |
| Y | 1,00 | 0,99 | 0,99 | -0,47 |
| X1 | 0,99 | 1,00 | 0,96 | -0,54 |
| X2 | 0,99 | 0,96 | 1,00 | -0,38 |
| X3 | -0,47 | -0,54 | -0,38 | 1,00 |
Особенностью многофакторной системы является недопустимость слишком тесной связи между факторными признаками. Это условие часто именуется проблемой коллинеарности факторов. Коллинеарность означает достаточно тесную неслучайною линейную корреляцию одних факторов с другими. Часто рекомендуют исключать фактор, связанный с другим фактором при 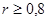 . Так же есть рекомендации исключать фактор уже при
. Так же есть рекомендации исключать фактор уже при 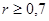 . Мы будем придерживаться варианта не более 0,7.
. Мы будем придерживаться варианта не более 0,7.
Из матрицы видно, что факторы Y, X1, X2 сильно коррелируют между собой. Фактор X3 слабо влияет на все остальные, поэтому его сразу можно исключить.
Оставляем факторы Y и X1.
Также для сравнения рассчитаем подобную корелляционую матрицу, но через относительные поазатели.
| год | Всего безработных, Y | мужчин, Х1 | женщин, Х2 | Время, X3=t |
| 1995 | 8,81165 | 8,193124 | 8,03786623 | 0 |
| 1996 | 8,81463 | 8,205765 | 8,02943284 | 0,69314718 |
| 1997 | 8,99442 | 8,382747 | 8,2125684 | 1,09861229 |
| 1998 | 9,09403 | 8,474703 | 8,32117831 | 1,38629436 |
| 1999 | 9,11537 | 8,47658 | 8,36474107 | 1,60943791 |
| 2000 | 8,85352 | 8,237744 | 8,07682603 | 1,79175947 |
| 2001 | 8,74878 | 8,134761 | 7,9700493 | 1,94591015 |
| 2002 | 8,74321 | 8,127109 | 7,9665867 | 2,07944154 |
| 2003 | 8,69131 | 8,054523 | 7,93844555 | 2,19722458 |
| 2004 | 8,71866 | 8,031385 | 8,01961279 | 2,30258509 |
|
| Y | X1 | X2 | X3 |
| Y | 1,00 | 0,99 | 0,99 | -0,29 |
| X1 | 0,99 | 1,00 | 0,95 | -0,35 |
| X2 | 0,99 | 0,95 | 1,00 | -0,21 |
| X3 | -0,29 | -0,35 | -0,21 | 1,00 |
Зависимость коэффициентов уменьшилась по сравнению с предыдущей матрицей, но общая зависимость факторов практически не изменилась.
Прежде чем начать анализ, построим график зависимости Y и X1, а также проведем тренд:
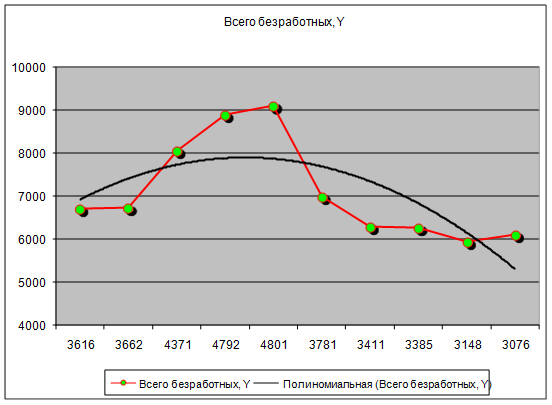
Из графика видно, что между экономическими явлениями существует нелинейное соотношение. Таким образом она выражена с помощью нелинейной регрессии, следующим полиномом:
y = a + b*x + c*x2
Для нашей параболы второй степени заменяем переменные x=x1, x2=x2, и получаем двухмерное уравнение линейной регрессии:
y = a + b*x1 + c*x2
Для оценки параметров линейной множественной регрессии используем метод наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.
Согласно МНК неизвестные параметры a,b и c получают таким образом, чтобы сумма квадратов отклонений фактических значений y от значений yр, найденных по уравнению регрессии, была минимальной:
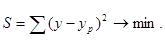
Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров a,b и c и приравнять их к нулю, тогда:
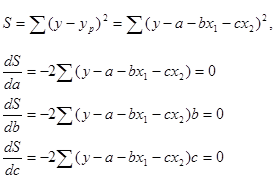
В результате преобразования получим следующую систему нормальных уравнений для оценки параметров a, b и с:
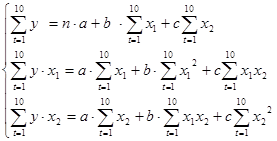
| t | y | x1 | y*x1 | (x1)^2 | x1*x2 | (x1)^4 | (x1^2)*Y |
| 1 | 6712 | 3616 | 24270592 | 13075456 | 47280848896 | 170967549607936 | 87762460672 |
| 2 | 6732 | 3662 | 24652584 | 13410244 | 49108313528 | 179834644139536 | 90277762608 |
| 3 | 8058 | 4371 | 35221518 | 19105641 | 83510756811 | 365025518020881 | 153953255178 |
| 4 | 8902 | 4792 | 42658384 | 22963264 | 110039961088 | 527311493533696 | 204418976128 |
| 5 | 9094 | 4801 | 43660294 | 23049601 | 110661134401 | 531284106259201 | 209613071494 |
| 6 | 6999 | 3781 | 26463219 | 14295961 | 54053028541 | 204374500913521 | 100057431039 |
| 7 | 6303 | 3411 | 21499533 | 11634921 | 39686715531 | 135371386676241 | 73334907063 |
| 8 | 6268 | 3385 | 21217180 | 11458225 | 38786091625 | 131290920150625 | 71820154300 |
| 9 | 5951 | 3148 | 18733748 | 9909904 | 31196377792 | 98206197289216 | 58973838704 |
| 10 | 6116 | 3076 | 18812816 | 9461776 | 29104422976 | 89525205074176 | 57868222016 |
| Сумма | 71135 | 38043 | 277189868 | 148364993 | 593427651189 | 2433191521665030 | 1108080079202 |
Получим систему:
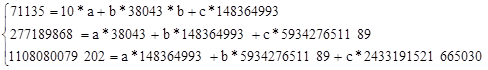
yр = 6368,97 - 1,34665*x + 0,0004x2
Посчитаем Yр. Сумма полученных отклонений расчетных значений от фактических должна быть равна 0.
| x1 | y(р) | Y | y-y(р) | (x1)^2 |
| 3616 | 6670,61 | 6712 | 41,39 | 45050944 |
| 3662 | 6741,07 | 6732 | -9,07 | 45319824 |
| 4371 | 8038,73 | 8058 | 19,27 | 64931364 |
| 4792 | 8997,42 | 8902 | -95,42 | 79245604 |
| 4801 | 9019,45 | 9094 | 74,55 | 82700836 |
| 3781 | 6931,10 | 6999 | 67,90 | 48986001 |
| 3411 | 6376,96 | 6303 | -73,96 | 39727809 |
| 3385 | 6342,10 | 6268 | -74,10 | 39287824 |
| 3148 | 6048,92 | 5951 | -97,92 | 35414401 |
| 3076 | 5968,65 | 6116 | 147,35 | 37405456 |
| Сумма полученных отклонений | 0,000 |
| ||
Дата: 2019-07-30, просмотров: 342.