Измерение физических величин
Измерение ФВ – совокупность операций по применению технического средства, хранящего единицу ФВ, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины. Под техническими средствами в данном случае следует понимать меры либо измерительные приборы. Так, прикладывая линейку с делениями к какому-либо предмету, сравнивают его размер с единицей, хранимой линейкой, и, произведя отсчет, получают значение величины (длины, высоты, толщины и других параметров предмета). С помощью вольтметра измеряют напряжение в вольтах, сравнивая размер измеряемой величины, преобразованной в перемещение указателя (стрелки вольтметра), с единицей, хранимой шкалой этого прибора.
Шкала ФВ – упорядоченная совокупность значений физической величины служащая исходной основой для измерений данной величины.
Различают пять основных типов шкал измерений: наименований (шкала классификации), порядка (шкала рангов), интервалов (шкала разностей), отношений, абсолютные. Шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений – метрическими (материальными). Практическая реализация шкал измерений осуществляется путём стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.


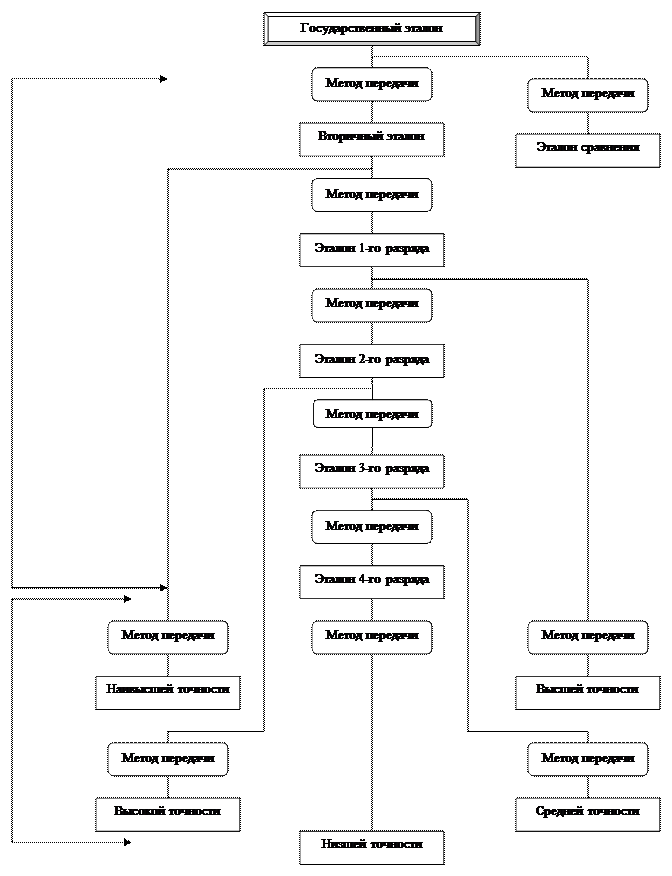

Рисунок 1- Государственная поверочная схема
Виды измерений
В метрологии существует множество видов (разновидностей) измерений и число их постоянно увеличивается.
Виды измерений определяются физическим характером измеряемой величины, требуемой точностью измерения, условиями и режимом измерений и т.д. Можно, например, выделить виды измерений в зависимости от их цели: контрольные, диагностические, лабораторные и технические, эталонные и поверочные и т.д.
В зависимости от способа получения числового значения измеряемой величины все измерения условно подразделяются на четыре основных вида: прямые, косвенные, совокупные и совместные.
Прямое измерение – измерение, при котором искомое значение физической величины получают непосредственно.
При прямых измерениях числовое значение измеряемой величины отсчитывается непосредственно по показаниям измерительных приборов. Символически прямое измерение может быть выражено формулой:
Y»X,
где Y - истинное значение измеряемой величины;
X- показание измерительного прибора.
К этому виду измерений относятся, например, измерения тока амперметром, напряжения источника - вольтметром и т.д.
Косвенное измерение – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. К этому виду измерений относится, например, косвенное измерение сопротивления резистора R путем прямых измерений напряжения и тока, связанных с искомой величиной сопротивления зависимостью:
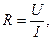
где R - сопротивление, Ом;
u - напряжение, В;
I - ток, А.
Измерение мощности постоянного тока амперметром и вольтметром с использованием зависимости, связывающей мощность постоянного тока с током и напряжением, а также нахождение плотности тела по его массе и геометрическим размерам следует отнести к косвенным измерениям.
Совокупными измерениями называются производимые одновременно измерения нескольких одноименных (однородных) величин, при которых искомые значения величин определяют путём решения системы уравнений, получаемых при измерении этих величин в различных сочетаниях. Пример совокупного измерения: измерение сопротивлений резисторов, соединенных треугольником, путем измерений сопротивлений между различными вершинами треугольника; по результатам трех измерений определяют сопротивления резисторов.
При совместных измерениях производятся одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними. Результат измерений получают путем решения системы уравнений.
По характеру точности различаются равноточные и неравноточные измерения.
Равноточные измерения – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений и в одних и тех же условиях c одинаковой тщательностью.
Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
По количеству измерительной информации различают однократные и многократные измерения.
Однократное измерение – измерение, выполненное один раз. Недостатком этих измерений является возможность грубой ошибки – промаха. Для предотвращения этого рекомендуется (при возможности) проводить не менее 2-3-х измерений и за результат измерений принимать их среднее значение. Во многих случаях на практике выполняются именно однократные измерения. Например, измерение конкретного момента времени по часам обычно проводится один раз.
Многократное измерение - измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т.е. состоящее из ряда однократных измерений. Обычно их число n³3. Многократные измерения проводят с целью уменьшения влияния случайных факторов на результат измерений.
По характеру изменения получаемой информации в процессе измерений измерения разделяются на статические и динамические измерения.
Статическое измерение - измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Они проводятся при практическом постоянстве измеряемой величины.
Пример. Средство измерений работает в статическом режиме. Выходной сигнал средства измерений, например, отклонение указателя, остается неизменным в течение времени использования выходного сигнала, следовательно, измерение - статическое.
К статическим измерениям можно отнести измерения размеров детали, измерения напряжения и сопротивления резистора постоянного тока. Пределы допускаемых отклонений не существенны по отношению к номинальному значению измеряемой величины.
Динамическое измерение - измерение изменяющейся по размеру физической величины, для получения результата измерения которой необходимо учитывать это изменение. К этим измерениям можно отнести измерение переменного тока, измерение параметров периодических и апериодических сигналов. Результат измерений в этом случае представляется изменяющейся во времени величиной и представляется совокупностью ее значений с указанием моментов времени, которым соответствуют эти значения.
По метрологическому назначению используемых средств измерений измерения подразделяются на технические и метрологические.
Технические измерения - измерения с помощью рабочих средств измерений.
Метрологические измерения - измерения при помощи эталонных средств измерений с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.
По отношению к основным единицам измерения делятся на абсолютные измерения и относительные измерения.
Абсолютное измерение - измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Абсолютное измерение рассматривается как измерение величины в ее единицах.
Относительное измерение - измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.
Пример. Измеритель скорости у сверхзвукового самолета, показывающий отношение скорости самолета к скорости звука, или указатель расхода бензина в автомобилях проводят относительные измерения указанных величин.
В метрологической практике под видом измерений понимают часть области измерений, имеющую свои особенности и отличающуюся однородностью измеряемых величин. Например, измерения геометрических, механических, электрических и магнитных величин, измерения электрического сопротивления, электродвижущей силы и др. Им присваивают коды, например: 27 – измерения геометрических величин; 28 – измерения механических величин и т.д.
Методы измерений
Взаимодействие СИ с объектом при измерении основано на физических явлениях, совокупность которых составляет принцип измерений, а совокупность приемов использования принципов и СИ называется методом измерений.
Принцип измерений – физическое явление или эффект, положенные в основу измерений. Например, применение пьезоэлектрического эффекта при измерении Э.Д.С. (электрического напряжения); эффект Холла при измерении сопротивления; эффект Доплера при измерении скорости; эффект Джозефсона для измерения электрического напряжения.
Метод измерений это прием или совокупность приемов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Например, измерение постоянного тока методом непосредственной оценки может быть выполнено на основе механического взаимодействия магнитного поля и измеряемого тока; определение напряженности поля производится на основе использования явления электромагнитной индукции, путем оценки значения э.д.с., которая индуцируется в антенне под действием измеряемого поля. Метод измерений обычно обусловлен устройством средств измерений и определяет способы решения измерительной задачи по принятой методике выполнения измерений (МВИ). Под методикой понимают технологию выполнения измерений (совокупность операций) с целью наилучшей реализации метода.
Для прямых измерений, где физический принцип, как правило, однозначно определяется принципом действия используемого СИ, совокупность методических приёмов (содержание метода) носит метрологический характер. Такие общие приёмы, называемые методами прямых измерений, позволяют в ряде случаев исключать или компенсировать наиболее существенные систематические погрешности измерений.
По способу сравнения измеряемой величины с её единицей методы прямых измерений подразделяют на метод непосредственной оценки («шкальный») и метод сравнения с мерой (рис.2).
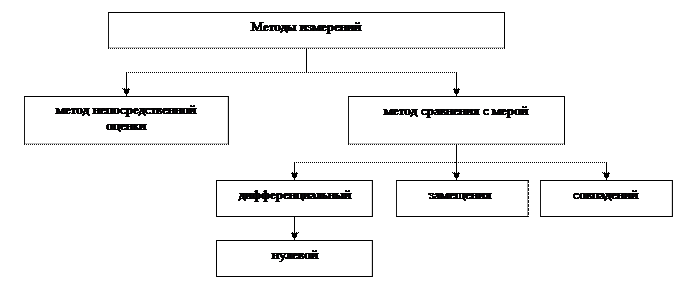

Рисунок 2
Метод сравнения с мерой имеет ряд разновидностей, отличающихся приёмами и способами сравнения.
При измерениях методом непосредственной оценки значение измеряемой величины определяют непосредственно по отсчетному устройству средства измерений, шкала которого заранее была проградуирована в единицах измеряемой величины.
К достоинствам метода непосредственной оценки можно отнести быстроту получения результата измерений и возможность непосредственного наблюдения за изменениями измеряемой величины, а к недостаткам то, что точностные возможности ограничены погрешностями градуировки СИ.
Метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
Отличительной чертой методов сравнения является непосредственное участие в процессе измерения меры известной величины, однородной с измеряемой. Сравнение может быть непосредственным или опосредствованным через другие величины, однозначно связанные с первыми.
Группа методов сравнения с мерой включает: нулевой, дифференциальный, замещения и совпадений.
Нулевой метод измерений - метод сравнения с мерой, в котором результирующей эффект воздействия измеряемой величины и (встречного воздействия) меры на прибор сравнения доводят до нуля.
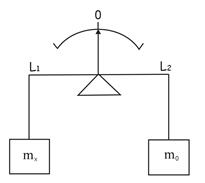
При нулевом методе измерений разность измеряемой величины и известной величины или разность эффектов, производимых измеряемой и известной величинами, сводится в процессе измерения к нулю, что фиксируется высокочувствительным прибором - нуль-индикатором. Нулевой метод широко используют при измерении массы на равноплечих весах (рис.3,а); при измерении сопротивления, индуктивности и емкости мостовыми схемами или тока и напряжения компенсационными устройствами.
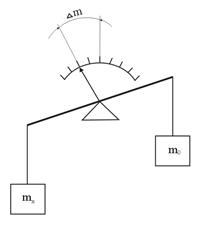
Дифференциальный метод - метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.
Дифференциальный метод измерений на примере, приведенном на рис.3,б, состоит в том, что измеряемая величина mХ сравнивается с известной величиной m0, воспроизводимой мерой, и полученная разность D m отсчитывается по шкале весов, градуированной в единицах массы. Таким образом, в отличие от нулевого метода в этом случае измеряемая величина уравновешивается не полностью. Значение измеряемой величины mХ определяется по известной величине m0 и измеренной разности Dm. Следовательно, mХ = m0 + D m, где D m – показания весов.
| 
| 
|
| Рисунок 3, а | Рисунок 3, б | Рисунок 3, в |
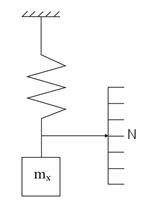
Метод замещения – метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.
Например, взвешивание на пружинных весах (рис.3,в). Измерение производят в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов; затем массу тx замещают массой гирь тo, подбирая ее так, чтобы указатель весов установился точно в том же положении, что и в первом случае. При этом ясно, что тx = тo . Метод замещения применяется при прецизионных измерениях сопротивления, индуктивности и емкости, при измерении напряженности поля и в ряде других случаев.
Метод совпадений - метод сравнения с мерой, при котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют по совпадению отметок шкал или периодических сигналов. Метод совпадений основывается на использовании совпадения отметок шкал, либо частоты сигналов, либо разности хода и т. д. По принципу данного метода построены такие измерительные приборы, как простая линейка, нониус штангенциркуля, резонансные частотомеры, различные интерферометры, а также приборы, использующие стробоскопический эффект. Например, шкала нониуса имеет десять делений по 0,9 мм, в то время как основная шкала штангенциркуля имеет обычную цену деления в 1 мм. Если начальная отметка шкалы нониуса не совпадает точно с какой-либо отметкой шкалы штангенциркуля, то это означает, что измеряемая длина имеет значение; не выражаемое целым числом. Долю миллиметра находят по совпадению какого-нибудь другого деления нониуса с отметкой основной шкалы. Таким образом, использование дополнительной шкалы (нониуса) позволяет тем же методом совпадения увеличить точность простой миллиметровой измерительной линейки на порядок (в десять раз).
В целом, достоинством группы методов сравнения с мерой является высокая точность измерений, а недостатком - сложность. Выбор того или иного метода измерений определяется назначением их результатов, требованиям к их быстроте и точности.
Результаты измерений
В соответствии с РМГ 29-99 результат измерений физической величины – значение величины, полученное путём её измерения.
Для характеристики качества измерений (кроме погрешности измерений) пользуются такими понятиями как сходимость и воспроизводимость результатов измерений.
Сходимость результатов измерений – близость друг другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.
Воспроизводимость результатов измерений – близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведённых к одним и тем же условиям измерений (температуре, давлению, влажности и др.)
Погрешности измерений
Любое измерение, как бы тщательно и аккуратно оно ни проводилось, сопровождается погрешностями получения результата. Их возникновение зависит от многих причин: качества изготовления средств измерений, их состояния при эксплуатации; от точности эталонных средств, по которым проводится их поверка; от изменения свойств объекта измерения, от температуры, влажности, атмосферного давления, сотрясений почвы, зданий и от других внешних факторов; от алгоритмов вычислений; от опыта и внимательности лиц, проводящих измерение; от применяемого метода (схемы) измерения и т.д. Поэтому результат измерений практически всегда отличается от истинного значения физической величины - значения, которое выражает размер величины идеальным образом.
Таким образом, результат измерения представляет собой приближенную оценку истинного значения величины, найденную путем измерения.
Отклонение результата измерения от истинного (действительного) значения измеряемой величины называют погрешностью результата измерения D:
D = Хизм – Хд,
где Хизм – измеренное значение величины, Хд – истинное (действительное) значение измеряемой величины.
Истинное значение физической величины неизвестно и применяется только в теоретических исследованиях. На практике вместо истинного значения ФВ пользуются её оценкой, полученной при обработке результатов наблюдений, или действительным значением величины, за которое принимают показание эталонных средств измерений.
Часто применяют понятие «точность измерения», имея в виду качество измерения, отражающее близость результата измерения к истинному значению измеряемой величины. Высокая точность измерения соответствует малым значениям погрешностей измерений.
Количество факторов, влияющих на точность измерения, достаточно велико, и любая классификация погрешностей измерений является условной. Но для практических целей в ГСИ принято за основную классификацию принимать следующую:
- по форме числового выражения: абсолютные и относительные;
- по закономерности проявления: систематические, случайные, грубые промахи.
По источникам возникновения погрешности подразделяют на: инструментальные, методические и субъективные (личные). Но какие бы разновидности погрешности измерений не рассматривались при анализе конкретной измерительной задачи, в них всегда можно выделить систематическую и случайную составляющие и выразить числом в абсолютной или относительной форме.
Дата: 2019-07-30, просмотров: 381.