Часть I. метрология
Метрология как деятельность
Обеспечение качества - одно из приложений метрологии как практической. В общем же случае метрология играет и познавательную, и созидательную роль в жизни общества.
Измерения осуществлялись и развивались от глубокой древности до наших дней.
Измерительные технологии применяются во всех без исключения сферах деятельности человека:
от торговли до навигации, здравоохранения и биологии;
от криминалистики и экологии до фундаментальных наук и промышленного производства;
от психофизиологии до землепользования, агротехники и разведки природных ресурсов.
В той или иной форме измерениями занимается практически всё население планеты. Или, другими словами, нет такой сферы общественной жизни, которая была бы свободна от измерений. Почти невозможно выбрать объект не доступный измерению.
Давно известно, что развитие теорий и их практическое применение немыслимы без первичной информации, получаемой путём измерений в процессе научного познания. Измерения распространены также как и математические методы и вычисления. И метрология, и математика рождались, развивались в тесной взаимосвязи. Но в силу отличительных особенностей у метрологии есть и своё место в науке.
Во-первых, получение достоверной измерительной информации немыслимо без привлечения арсенала метрологии. Это и методические приёмы по измерению, обработке результатов измерений, по оценке достоверности полученных результатов. Т.е. вся технология получения достоверной первичной информации о свойствах исследуемых объектов или явлений.
Во-вторых, многоплановая социальная значимость обеспечения единства измерений - было и остаётся естественной государственной монополией и осуществляется при поддержке и под надзором государственных органов управления.
В-третьих, метрология взаимосвязана в общей системе наук. Теория измерений имеет все признаки математической дисциплины. Методы измерений, воспроизведение единиц величин и шкал прочно связаны с естественными науками (физика, химия...). Прикладная метрология использует достижения технических дисциплин в области приборостроения. Законодательная метрология имеет признаки юриспруденции.
Таким образом, результаты измерений, получаемые от метрологической деятельности:
составляют объективную основу информации, необходимой для принятия решений и управления;
сопровождают каждое новое открытие в науке, лежащее в основе физических или химических явлений, а также в других областях;
уточняют многие неправильные выводы и заключения, которые были сделаны ранее на основе наблюдений за явлениями природы;
широко применяются в технике, народном хозяйстве, торговле;
служат основой для управления технологическими процессами при изготовлении продукции;
служат основой для оценки качества продукции.
Массовость и значимость измерений определяют многообразие видов практической метрологической деятельности:
обеспечение единства измерений;
воспроизведение единиц величин;
передача информации о размерах единиц;
разработка и изготовление средств измерений;
поверка и калибровка средств измерений;
метрологическое обеспечение производства;
метрологическое обеспечение систем качества;
метрологическая экспертиза технической документации;
Государственный метрологический контроль и надзор
и другие.
Физические величины
Физическая величина (ФВ) – одно из свойств физического объекта (физической системы, явления или процесса) общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них.
Между измеряемыми физическими величинами существуют связи и зависимости, выражаемые математическими соотношениями и формулами. Такие величины образуют систему.
Система величин – это совокупность физических величин, образованная в соответствии с принятыми принципами, когда одни величины принимают за независимые, а другие определяют как функции независимых величин.
Физическая величина, входящая в систему и условно принятая в качестве независимой от других величин системы, называется основной физической величиной, а ее единица - основной единицей системы единиц физических величин. За основные выбраны величины, которые могут быть воспроизведены и измерены с наиболее высокой точностью для достигнутого на современном этапе уровня развития техники.
Производная физическая величина - физическая величина, входящая в систему и определяемая через основные величины этой системы, а ее единица называется производной и образуется в соответствии с уравнением, связывающим эту единицу с основными единицами.
Зависимость каждой производной величины от основных отображается ее размерностью.
Размерность является формализованным отражением качественного различия измеряемых величин. Она определяет «род» ФВ. Например, длина – протяженность, присущая любому объекту; электрическое сопротивление – как общее свойство проводников электричества.
Размерность обозначается символом dim, происходящим от слова dimension, которое переводится - размерность.
Размерность основных физических величин обозначается соответствующими заглавными буквами, принятыми в международной практике. Для длины, массы и времени, например,
dim l =L; dim m = M; dim t = T
В общем случае размерность выражается в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях и отражающего связь данной ФВ с физическими величинами, принятыми в данной системе величин за основные с коэффициентом пропорциональности равным единице.
dim Q = Lα M β T γ …,
где dim Q – размерность какой-либо физической величины Q;
L, M, T … - размерности основных физических величин;
α, β, γ … - показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулем.
Формула размерности основной величины совпадает с ее символом.
dim l = Lα M β ∙T γ…= L 1 ∙M 0 ∙T 0… = L
Размерность величин определяют на основе соответствующих уравнений физики.
Физическая величина является размерной, если в ее размерность входит хотя бы одна из основных величин, возведенная в степень, не равную нулю. Большинство физических величин являются размерными. Однако имеются безразмерные (относительные) величины, представляющие собой отношение данной физической величины к одноименной, применяемой в качестве исходной (опорной). В этом случае основные физические величины входят в размерность в степени, равной нулю.
Безразмерными величинами являются, например, коэффициент трансформации, затухания и т.д.
Одна и та же размерность может быть присуща величинам, имеющим разную исходную качественную природу и различающимся по форме определяющего уравнения из физики, например для величин, приведенных в таблице 2.
Таблица 2
| A = F∙ l | A = i ∙U∙ t |
| где А – работа; F – сила; l – длина; | где i –сила тока; U–напряжение; t– время |
| dim A=dim F∙ dim l; | dim A =dim i ∙ dim U∙ dim t |
| dim l = L; dim F = dim m∙ dim a; | dim i = I; dim t =T; |
| dim m=M; dim a= dim l∙ dim -2 t= L∙T-2 | dim U= L2∙ M∙ T-3 I-1 |
| dim F = L∙ M∙ T-2 | dim -1 t = T-1 |
| dim A= L2 ∙M ∙T-2 | dim A= L2 ∙M ∙T-2 |
Над размерностью можно производить действия умножения, деления, возведения в степень и извлечение корня. Понятие размерность широко используется:
- для перевода единиц из одной системы в другую;
- для проверки правильности сложных расчетных формул, полученных в результате теоретического вывода;
- при выяснении зависимости между величинами;
- в теории физики (физического подобия).
Количественной характеристикой ФВ является размер. Например, длина конкретного предмета; сопротивление конкретного резистора. Размер существует объективно, независимо от того, знаем мы его или нет.
Размер ФВ – количественная определенность ФВ, присущая конкретному материальному объекту, системе, явлению или процессу. Размер ФВ – это количественное содержание в данном объекте свойства, соответствующего понятию ФВ. Например, все тела можно различать по массе, т.е. по размеру интересующей нас ФВ.
Размер нужно отличать от значения.
Значение ФВ – это выражение размера ФВ в виде некоторого числа принятых для нее единиц. Его получают в результате измерений ФВ или вычислений в соответствии с основным уравнением измерений и выражают в форме:
Q = n • [Q], (1)
где Q – значение ФВ;
n – числовое значение;
[Q] – выбранная единица.
Уравнение (1) называется основным уравнением измерения. Оно показывает, что числовое значение ФВ зависит от размера принятой единицы измерений, тогда как размер ФВ будет одним и тем же.
Например, если:
1) масса измеряется в принятой единице измерений – килограмм (кг), тогда размер массы выражается значением равным 10 кг;
2) масса измеряется в граммах (г) и ее размер (для того же случая) будет выражаться значением равным 10 000 г.
Числовое значение ФВ - это отвлеченное число, входящее в значение величины. Например, 20 кг. Значение ФВ – 20 кг, 20 - числовое значение, кг – единица физической величины.
Истинное значение ФВ, значение ФВ, которое идеальным образом характеризует в количественном и качественном отношении соответствующую ФВ. Истинное значение может быть получено при бесконечно большом числе измерений и бесконечном совершенствовании метода и средства измерений.
Действительное значение ФВ - значение ФВ, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Единицы физических величин
Единица физической величины (ЕФВ) – физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице, и применяемая для количественного выражения однородных с ней физических величин. Единица физической величины – величина того же рода, что и сама физическая величина. Например: 1 м – единица длины; 1 с – единица времени; 1 А – единица силы электрического тока и т. д.
Размер ЕФВ устанавливается путем их законодательно закрепленного определения метрологическими органами государства.
Например - метр есть длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 долей секунды.
Килограмм – единица массы, равная массе международного прототипа килограмма.
Секунда – единица времени, равная 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома Цезия – 133.
Ампер – сила не изменяющегося тока, который, проходя по двум прямолинейным параллельным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным на расстоянии одного метра один от другого в вакууме, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10-7 ньютона.
Кельвин – единица термодинамической температуры, 1/273,16 части термодинамической температуры тройной точки воды.
Кандела – единица силы света, равная силе света в заданном направлении источника, испускающее монохроматическое излучение 540·1012 герц (540 ТГц), энергетическая сила света которого в этом направлении составляет 1/683 Ватт на стерадиан.
Моль – единица количества вещества, равная количеству вещества системы, в которой содержится столько же структурных элементов( атомов, молекул, ионов, электронов и других частиц или специфицированных групп частиц) сколько содержится атомов в Углероде – 12 массой 0,012 килограмма.
Единицы измерений во всех странах узакониваются директивным методом (закон, декрет Правительства). На основании федерального закона «Об обеспечении единства измерений» на территории РФ введены к использованию единицы Международной системы единиц (SI), принятой Генеральной конференцией по мерам и весам, рекомендованной Международной организацией законодательной метрологии, которые применяются в соответствии с национальным стандартом ГОСТ 8.417-2002 «ГСИ. Единицы величин».
Так же как и величины, единицы величин подразделяются на основные и производные. Совокупность основных и производных единиц, используемых для измерений всех физических величин, образует систему единиц.
Единица физической величины, входящая в принятую систему единиц, называется системной единицей. Основные, производные, кратные и дольные единицы системы SI являются системными. Например: 1 м; 1 м/с; 1 нм.
Единица физической величины, не входящая в принятую систему единиц, называется внесистемной единицей. Внесистемные единицы (по отношению к единицам SI) разделяются на четыре группы:
- допускаемые наравне с единицами SI: единица массы – тонна; единица вместимости – литр; единицы времени – минута, сутки, неделя, месяц, год, век и др.;
- допускаемые к применению в специальных областях: в астрономии – световой год (св.год), парсек (пс) – единица длины; в оптике диоптрия (дптр) – единица оптической силы; в сельском хозяйстве – гектар (га) – единица площади; в геодезии – град или гон – единица плоского угла и др.;
- временно допускаемые: миля – единица длины (1 миля); оборот в секунду – единица скорости (1 об/с); карат – единица массы (1 кар); бар – единица давления (1 бар) и др.;
- изъятые из употребления – лошадиная сила – единица мощности (1 л.с.); единица давления – килограмм-сила на квадратный сантиметр (1 кгс/см 2); эрг – единица работы, энергии (1 эрг) и др.
Системы единиц величин
Система единиц физических величин - совокупность основных и производных единиц физических величин, образованная в соответствии с принципами для заданной системы физических величин.
Для электрических и магнитных измерений на практике известно несколько систем единиц:
Абсолютная система единиц СГС, основными единицами которой являются сантиметр, грамм, секунда и в которой электрическая постоянная eo и магнитная постоянная m0 при не рационализированной форме уравнений электромагнитного поля равны единице;
Абсолютная практическая система МКСА, основными единицами которой являются метр, килограмм, секунда и ампер ;
Международная система единиц СИ (SI), основными единицами которой являются: метр, килограмм, секунда, ампер, кельвин, кандела, моль.
Наиболее предпочтительной является система SI, имеющая ряд достоинств:
- универсальность – охват всех областей науки и техники;
- унификация единиц для всех областей и видов измерений (механических, тепловых, электрических, магнитных и т. д.);
- когерентность единиц – все производные единицы SI получаются из уравнений связи между величинами, в которых коэффициенты равны единице;
- возможность воспроизведения единиц с высокой точностью в соответствии с их определениями;
- упрощение записи уравнений и формул в физике, химии, а также в технических расчетах в связи с отсутствием переводных коэффициентов;
- уменьшение числа допускаемых единиц;
- единая система образования кратных и дольных единиц, имеющих собственные наименования.
В соответствии с ГОСТ 8.417-2002 «ГСИ. Единицы величин», система SI, принятая в качестве национальной, включает семь основных единиц, приведенных в таблице3.
Производная единица – это единица производной физической величины системы единиц, образованная в соответствии с уравнениями, связывающими ее с основными единицами или с основными и уже определенными производными. Производные единицы системы SI имеют собственные названия. Примеры производных единиц приведены в таблице 4.
Таблица 3 - Основные величины и основные единицы физических величин
| Величина | Единица величины | ||||
| наименование | обозначение | размерность (символ) | наимено- | обозначение | |
| русское | между- народное | ||||
| Длина | l | L | метр | м | m |
| Масса | m | M | килограмм | кг | kg |
| Время | t | T | секунда | с | s |
| Сила электрического тока | i | I | ампер | А | A |
| Термодинамическая температура | T | Θ | кельвин | К | K |
| Сила света | J | J | кандела | кд | kd |
| Количество вещества | n | N | моль | моль | mol |
Таблица 4 - Производные величины и производные единицы
| Величина | Единица величины | ||||
| наименование | обозначение | размерность | наименование | обозначение | выражение производной единицы через основные |
| Частота | f | T-1 | герц | Гц | с-1 |
| Сила | F | LMT -2 | ньютон | Н | м кг·с -2 |
| Давление | Р | L-1MT-2 | паскаль | Па | м-1 ·кг с -2 |
| Работа | А | L2MT-2 | джоуль | Дж | м2 кг с-2 |
| Мощность | N | L2MT-3 | ватт | Вт | м2 кг с-3 |
Производные единицы бывают когерентными и некогерентными.
Когерентной называется производная единица физической величины, связанная с другими единицами системы уравнением, в котором числовой множитель принят равным единице. Все остальные производные единицы относятся к некогерентным.
Кратные и дольные единицы
Числовые значения физических величин изменяются в значительных пределах. Поэтому для удобства практических измерений наряду с основными и производными единицами, называемыми главными, введены также кратные и дольные единицы, которые обычно находятся в декадном отношении к главной единице. Кратные и дольные единицы образуются добавлением соответствующих приставок к главной единице согласно таблице 5.
Например: 1 пФ (пикофарада) = 10-12 Ф; наносекундный импульс - импульс, длительность которого 10-9 с; 1 мкВ (микровольт) =10-6 В и т.д.
Таблица 5 - Приставки для образования кратных и дольных единиц
| Кратные единицы |
Дольные единицы
Рисунок 1- Государственная поверочная схема
Виды измерений
В метрологии существует множество видов (разновидностей) измерений и число их постоянно увеличивается.
Виды измерений определяются физическим характером измеряемой величины, требуемой точностью измерения, условиями и режимом измерений и т.д. Можно, например, выделить виды измерений в зависимости от их цели: контрольные, диагностические, лабораторные и технические, эталонные и поверочные и т.д.
В зависимости от способа получения числового значения измеряемой величины все измерения условно подразделяются на четыре основных вида: прямые, косвенные, совокупные и совместные.
Прямое измерение – измерение, при котором искомое значение физической величины получают непосредственно.
При прямых измерениях числовое значение измеряемой величины отсчитывается непосредственно по показаниям измерительных приборов. Символически прямое измерение может быть выражено формулой:
Y»X,
где Y - истинное значение измеряемой величины;
X- показание измерительного прибора.
К этому виду измерений относятся, например, измерения тока амперметром, напряжения источника - вольтметром и т.д.
Косвенное измерение – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. К этому виду измерений относится, например, косвенное измерение сопротивления резистора R путем прямых измерений напряжения и тока, связанных с искомой величиной сопротивления зависимостью:
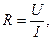
где R - сопротивление, Ом;
u - напряжение, В;
I - ток, А.
Измерение мощности постоянного тока амперметром и вольтметром с использованием зависимости, связывающей мощность постоянного тока с током и напряжением, а также нахождение плотности тела по его массе и геометрическим размерам следует отнести к косвенным измерениям.
Совокупными измерениями называются производимые одновременно измерения нескольких одноименных (однородных) величин, при которых искомые значения величин определяют путём решения системы уравнений, получаемых при измерении этих величин в различных сочетаниях. Пример совокупного измерения: измерение сопротивлений резисторов, соединенных треугольником, путем измерений сопротивлений между различными вершинами треугольника; по результатам трех измерений определяют сопротивления резисторов.
При совместных измерениях производятся одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними. Результат измерений получают путем решения системы уравнений.
По характеру точности различаются равноточные и неравноточные измерения.
Равноточные измерения – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений и в одних и тех же условиях c одинаковой тщательностью.
Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
По количеству измерительной информации различают однократные и многократные измерения.
Однократное измерение – измерение, выполненное один раз. Недостатком этих измерений является возможность грубой ошибки – промаха. Для предотвращения этого рекомендуется (при возможности) проводить не менее 2-3-х измерений и за результат измерений принимать их среднее значение. Во многих случаях на практике выполняются именно однократные измерения. Например, измерение конкретного момента времени по часам обычно проводится один раз.
Многократное измерение - измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т.е. состоящее из ряда однократных измерений. Обычно их число n³3. Многократные измерения проводят с целью уменьшения влияния случайных факторов на результат измерений.
По характеру изменения получаемой информации в процессе измерений измерения разделяются на статические и динамические измерения.
Статическое измерение - измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Они проводятся при практическом постоянстве измеряемой величины.
Пример. Средство измерений работает в статическом режиме. Выходной сигнал средства измерений, например, отклонение указателя, остается неизменным в течение времени использования выходного сигнала, следовательно, измерение - статическое.
К статическим измерениям можно отнести измерения размеров детали, измерения напряжения и сопротивления резистора постоянного тока. Пределы допускаемых отклонений не существенны по отношению к номинальному значению измеряемой величины.
Динамическое измерение - измерение изменяющейся по размеру физической величины, для получения результата измерения которой необходимо учитывать это изменение. К этим измерениям можно отнести измерение переменного тока, измерение параметров периодических и апериодических сигналов. Результат измерений в этом случае представляется изменяющейся во времени величиной и представляется совокупностью ее значений с указанием моментов времени, которым соответствуют эти значения.
По метрологическому назначению используемых средств измерений измерения подразделяются на технические и метрологические.
Технические измерения - измерения с помощью рабочих средств измерений.
Метрологические измерения - измерения при помощи эталонных средств измерений с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.
По отношению к основным единицам измерения делятся на абсолютные измерения и относительные измерения.
Абсолютное измерение - измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Абсолютное измерение рассматривается как измерение величины в ее единицах.
Относительное измерение - измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.
Пример. Измеритель скорости у сверхзвукового самолета, показывающий отношение скорости самолета к скорости звука, или указатель расхода бензина в автомобилях проводят относительные измерения указанных величин.
В метрологической практике под видом измерений понимают часть области измерений, имеющую свои особенности и отличающуюся однородностью измеряемых величин. Например, измерения геометрических, механических, электрических и магнитных величин, измерения электрического сопротивления, электродвижущей силы и др. Им присваивают коды, например: 27 – измерения геометрических величин; 28 – измерения механических величин и т.д.
Методы измерений
Взаимодействие СИ с объектом при измерении основано на физических явлениях, совокупность которых составляет принцип измерений, а совокупность приемов использования принципов и СИ называется методом измерений.
Принцип измерений – физическое явление или эффект, положенные в основу измерений. Например, применение пьезоэлектрического эффекта при измерении Э.Д.С. (электрического напряжения); эффект Холла при измерении сопротивления; эффект Доплера при измерении скорости; эффект Джозефсона для измерения электрического напряжения.
Метод измерений это прием или совокупность приемов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Например, измерение постоянного тока методом непосредственной оценки может быть выполнено на основе механического взаимодействия магнитного поля и измеряемого тока; определение напряженности поля производится на основе использования явления электромагнитной индукции, путем оценки значения э.д.с., которая индуцируется в антенне под действием измеряемого поля. Метод измерений обычно обусловлен устройством средств измерений и определяет способы решения измерительной задачи по принятой методике выполнения измерений (МВИ). Под методикой понимают технологию выполнения измерений (совокупность операций) с целью наилучшей реализации метода.
Для прямых измерений, где физический принцип, как правило, однозначно определяется принципом действия используемого СИ, совокупность методических приёмов (содержание метода) носит метрологический характер. Такие общие приёмы, называемые методами прямых измерений, позволяют в ряде случаев исключать или компенсировать наиболее существенные систематические погрешности измерений.
По способу сравнения измеряемой величины с её единицей методы прямых измерений подразделяют на метод непосредственной оценки («шкальный») и метод сравнения с мерой (рис.2).
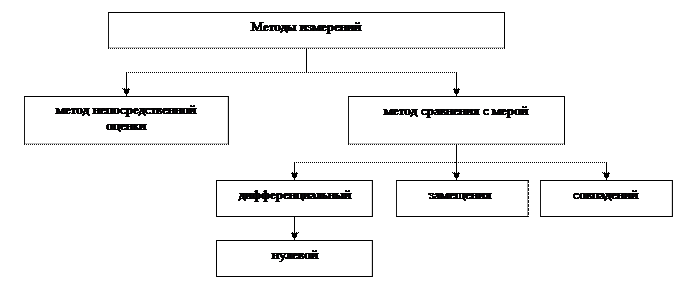
Рисунок 2
Метод сравнения с мерой имеет ряд разновидностей, отличающихся приёмами и способами сравнения.
При измерениях методом непосредственной оценки значение измеряемой величины определяют непосредственно по отсчетному устройству средства измерений, шкала которого заранее была проградуирована в единицах измеряемой величины.
К достоинствам метода непосредственной оценки можно отнести быстроту получения результата измерений и возможность непосредственного наблюдения за изменениями измеряемой величины, а к недостаткам то, что точностные возможности ограничены погрешностями градуировки СИ.
Метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
Отличительной чертой методов сравнения является непосредственное участие в процессе измерения меры известной величины, однородной с измеряемой. Сравнение может быть непосредственным или опосредствованным через другие величины, однозначно связанные с первыми.
Группа методов сравнения с мерой включает: нулевой, дифференциальный, замещения и совпадений.
Нулевой метод измерений - метод сравнения с мерой, в котором результирующей эффект воздействия измеряемой величины и (встречного воздействия) меры на прибор сравнения доводят до нуля.
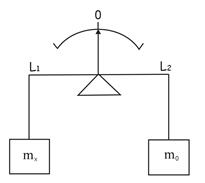
При нулевом методе измерений разность измеряемой величины и известной величины или разность эффектов, производимых измеряемой и известной величинами, сводится в процессе измерения к нулю, что фиксируется высокочувствительным прибором - нуль-индикатором. Нулевой метод широко используют при измерении массы на равноплечих весах (рис.3,а); при измерении сопротивления, индуктивности и емкости мостовыми схемами или тока и напряжения компенсационными устройствами.
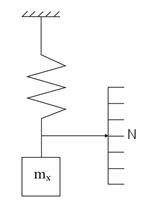
Дифференциальный метод - метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.
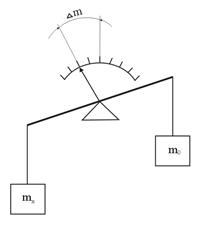
Дифференциальный метод измерений на примере, приведенном на рис.3,б, состоит в том, что измеряемая величина mХ сравнивается с известной величиной m0, воспроизводимой мерой, и полученная разность D m отсчитывается по шкале весов, градуированной в единицах массы. Таким образом, в отличие от нулевого метода в этом случае измеряемая величина уравновешивается не полностью. Значение измеряемой величины mХ определяется по известной величине m0 и измеренной разности Dm. Следовательно, mХ = m0 + D m, где D m – показания весов.
| 
| 
|
| Рисунок 3, а | Рисунок 3, б | Рисунок 3, в |
Метод замещения – метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.
Например, взвешивание на пружинных весах (рис.3,в). Измерение производят в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов; затем массу тx замещают массой гирь тo, подбирая ее так, чтобы указатель весов установился точно в том же положении, что и в первом случае. При этом ясно, что тx = тo . Метод замещения применяется при прецизионных измерениях сопротивления, индуктивности и емкости, при измерении напряженности поля и в ряде других случаев.
Метод совпадений - метод сравнения с мерой, при котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют по совпадению отметок шкал или периодических сигналов. Метод совпадений основывается на использовании совпадения отметок шкал, либо частоты сигналов, либо разности хода и т. д. По принципу данного метода построены такие измерительные приборы, как простая линейка, нониус штангенциркуля, резонансные частотомеры, различные интерферометры, а также приборы, использующие стробоскопический эффект. Например, шкала нониуса имеет десять делений по 0,9 мм, в то время как основная шкала штангенциркуля имеет обычную цену деления в 1 мм. Если начальная отметка шкалы нониуса не совпадает точно с какой-либо отметкой шкалы штангенциркуля, то это означает, что измеряемая длина имеет значение; не выражаемое целым числом. Долю миллиметра находят по совпадению какого-нибудь другого деления нониуса с отметкой основной шкалы. Таким образом, использование дополнительной шкалы (нониуса) позволяет тем же методом совпадения увеличить точность простой миллиметровой измерительной линейки на порядок (в десять раз).
В целом, достоинством группы методов сравнения с мерой является высокая точность измерений, а недостатком - сложность. Выбор того или иного метода измерений определяется назначением их результатов, требованиям к их быстроте и точности.
Результаты измерений
В соответствии с РМГ 29-99 результат измерений физической величины – значение величины, полученное путём её измерения.
Для характеристики качества измерений (кроме погрешности измерений) пользуются такими понятиями как сходимость и воспроизводимость результатов измерений.
Сходимость результатов измерений – близость друг другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.
Воспроизводимость результатов измерений – близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведённых к одним и тем же условиям измерений (температуре, давлению, влажности и др.)
Погрешности измерений
Любое измерение, как бы тщательно и аккуратно оно ни проводилось, сопровождается погрешностями получения результата. Их возникновение зависит от многих причин: качества изготовления средств измерений, их состояния при эксплуатации; от точности эталонных средств, по которым проводится их поверка; от изменения свойств объекта измерения, от температуры, влажности, атмосферного давления, сотрясений почвы, зданий и от других внешних факторов; от алгоритмов вычислений; от опыта и внимательности лиц, проводящих измерение; от применяемого метода (схемы) измерения и т.д. Поэтому результат измерений практически всегда отличается от истинного значения физической величины - значения, которое выражает размер величины идеальным образом.
Таким образом, результат измерения представляет собой приближенную оценку истинного значения величины, найденную путем измерения.
Отклонение результата измерения от истинного (действительного) значения измеряемой величины называют погрешностью результата измерения D:
D = Хизм – Хд,
где Хизм – измеренное значение величины, Хд – истинное (действительное) значение измеряемой величины.
Истинное значение физической величины неизвестно и применяется только в теоретических исследованиях. На практике вместо истинного значения ФВ пользуются её оценкой, полученной при обработке результатов наблюдений, или действительным значением величины, за которое принимают показание эталонных средств измерений.
Часто применяют понятие «точность измерения», имея в виду качество измерения, отражающее близость результата измерения к истинному значению измеряемой величины. Высокая точность измерения соответствует малым значениям погрешностей измерений.
Количество факторов, влияющих на точность измерения, достаточно велико, и любая классификация погрешностей измерений является условной. Но для практических целей в ГСИ принято за основную классификацию принимать следующую:
- по форме числового выражения: абсолютные и относительные;
- по закономерности проявления: систематические, случайные, грубые промахи.
По источникам возникновения погрешности подразделяют на: инструментальные, методические и субъективные (личные). Но какие бы разновидности погрешности измерений не рассматривались при анализе конкретной измерительной задачи, в них всегда можно выделить систематическую и случайную составляющие и выразить числом в абсолютной или относительной форме.
Систематические погрешности
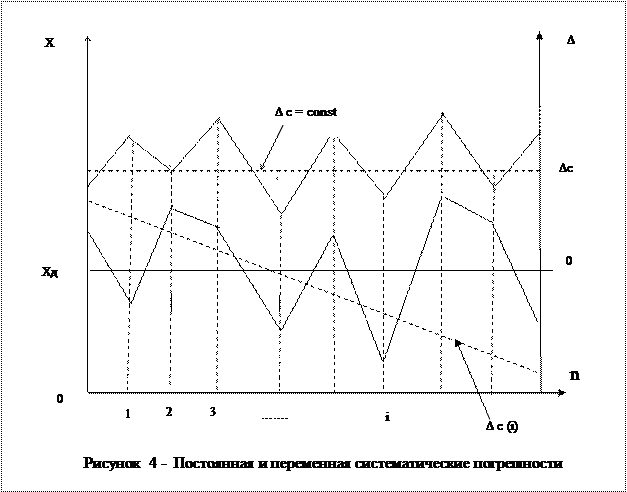
Систематическими погрешностями Dс называются составляющие погрешности измерения, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях одной и той же величины (рис. 4). Они возникают под действием отдельных определенных факторов - источников погрешностей. Примером систематических погрешностей являются погрешности показаний измерительных приборов вследствие их неправильной градуировки или изменения окружающей температуры.
Причиной появления систематических погрешностей также могут быть неисправности измерительной аппаратуры, несовершенство метода измерений, неправильная установка измерительных приборов и отступление от нормальных условий работы, особенно самого оператора. Систематические погрешности в принципе могут быть выявлены и устранены. Для этого требуется проведение тщательного анализа возможных источников погрешностей в каждом конкретном случае.
Если известны причины, вызывающие появление систематической погрешности, то её можно обнаружить при измерениях и исключить из результата полностью или частично введением соответствующих поправок или устранить изменением условий измерений, юстировкой, подгонкой меры и т.д.
Поправка определяется значением величины, одноименной с измеряемой, которую необходимо прибавить к измеренному значению с целью исключения систематической погрешности. Количественно поправка с равна абсолютной систематической погрешности, взятой с обратным знаком:
с = - Dс.
Однако систематическую составляющую погрешности удаётся исключить не полностью. Оставшуюся неустранённой из результатов систематическую погрешность называют неисключённой систематической погрешностью.
Случайные погрешности
Случайная погрешность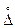 
– составляющая погрешности, изменяющаяся случайным образом при повторных измерениях одной и той же величины (рис. 5).
Случайная погрешность является результатом случайных изменений многочисленных условий измерений, учёт которых практически не осуществим, и её можно обнаружить только при многократных измерениях.
Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения. Их влияние может быть учтено теоретически, путём применения специальных способов обработки результатов наблюдений методами теории вероятностей и математической статистики.
Грубые промахи
Грубая погрешность (промах) – погрешность измерения, существенно превышающая ожидаемую при данных условиях погрешность.
|
|
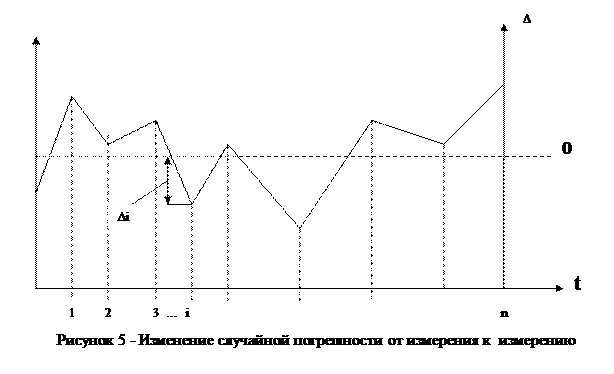
Причиной грубой погрешности может служить невнимательность оператора, неисправность прибора, кратковременные изменения условий измерения. Как правило, грубые погрешности выявляются в результате обработки результатов измерений с помощью специальных критериев.
Методические погрешности
Методические погрешности относятся к погрешностям, не зависящим от свойств используемых СИ. Факторы, вызывающие методические погрешности, самые разнообразные и зависят от области измерений (геометрические, радиотехнические, теплотехнические и др.), выбранного метода измерений, способов вычисления результатов измерений, различных допущений и упрощений в процессе измерения и др. При выборе метода измерений руководствуются их назначением, требуемой точностью результатов, удобствами использования и другими факторами.
Методические погрешности измерений могут возникнуть вследствие недостаточной разработанности теории тех явлений, которые положены в основу измерения, и неточности тех соотношений, которые используются для нахождения оценки измеряемой величины.
Субъективные погрешности
Субъективные погрешности вызываются состоянием оператора, проводящего измерения, его положением во время работы, несовершенством органов чувств, эргономическими свойствами средств измерений, недоработкой программного обеспечения современных измерительных систем. Всё это, как правило, сказывается на точности визирования и отсчёта.
В то же время широкое применение цифровых СИ, возможность их комплексного использования в автоматизированных системах измерений и обработки измерительной информации позволяет значительно уменьшить значения субъективных погрешностей.
Погрешности
Обозначение класса точности
Примечания
D- пределы допускаемой основной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы;
х – значение измеряемой величины на входе
(выходе) средств измерений или число делений, отсчитанных по шкале;
а и b–положительные числа, не зависящие от х.
0,5
Деятельность по ОЕИ осуществляется в соответствии с:
- Конституцией Российской Федерации (статья 71р);
- Законом РФ "Об обеспечении единства измерений";
- постановлением Правительства РФ от 12.02.94 № 100 «Об организации работ по стандартизации, обеспечению единства измерений, сертификации продукции и услуг»;
- НД ГСИ, принимаемыми и утверждаемыми Федеральным агентством по техническому регулированию и метрологии (Ростехрегулирование, бывший Госстандарт России).
Деятельность по ОЕИ осуществляется на:
- государственном уровне;
- уровне федеральных органов исполнительной власти;
- уровне юридического лица.
ОЕИ в пределах установленной ответственности федерального органа исполнительной власти и области деятельности юридического лица осуществляет метрологическая служба.
Метрологические службы
ОЕИ обеспечивается следующими субъектами метрологии:
- Государственной метрологической службой - (ГМС);
- метрологическими службами федеральных органов исполнительной власти и юридических лиц (МС).
В ГМС входят:
- подразделения центрального аппарата Госстандарта России, осуществляющие функции планирования, управления и контроля деятельности по ОЕИ на межотраслевом уровне;
- государственные научные метрологические центры (ГНМЦ);
- органы ГМС в субъектах РФ (на территориях республик в составе РФ, автономной области, автономных округов, краев, областей, округов и городов) – центры стандартизации и метрологии (ЦСМ).
Государственные научные метрологические центры представлены такими институтами, как ВНИИ метрологической службы (ВНИИМС, г. Москва), ВНИИ метрологии им. Д.И. Менделеева (ВНИИМ, г. Санкт-Петербург); НПО "ВНИИ физико-технических и радиотехнических измерений" (ВНИИФТРИ, пос. Менделеево Московской обл.); Уральский НИИ метрологии (УНИИМ, г. Екатеринбург) и др. Указанные научные центры не только занимаются разработкой научно-методических основ совершенствования российской системы измерений, но и являются держателями государственных эталонов.
В России функционирует около 90 ЦСМ (соответственно их метрологических подразделений), которые выполняют функции региональных органов ГМС на территориях субъектов РФ.
Ростехрегулирование осуществляет методическое руководство тремя государственными справочными службами: Государственной службой времени, частоты и определения параметров вращения Земли (ГСВЧ), Государственной службой стандартных образцов состава и свойств веществ и материалов (ГССО) и Государственной службой стандартных справочных данных о физических константах и свойствах веществ и материалов (ГСССД).
ГСВЧ осуществляет межрегиональную и межотраслевую координацию работ по обеспечению единства измерений времени, частоты и определения параметров вращения Земли. Об этой службе рядовой житель страны узнает 2 раза в год - при переходе на летнее и зимнее время. Потребителями измерительной информации ГСВЧ являются службы навигации и управления самолетами, судами и спутниками, Единая энергетическая система и пр.
ГССО обеспечивает создание и применение системы стандартных (эталонных) образцов состава и свойств веществ и материалов - металлов и сплавов, нефтепродуктов, медицинских препаратов, образцов почв, образцов твердости различных материалов, образцов газов и газовых смесей и др. Практическое значение СО показано выше.
ГСССД обеспечивает разработку достоверных данных о физических константах, о свойствах веществ и материалов, в том числе конструкционных материалов, минерального сырья, нефти, газа и др. Потребителями информации ГСССД являются организации, проектирующие изделия техники, к точности характеристик которых предъявляются особо жесткие требования. Конструкторы этой техники не могут полагаться на противоречивую информацию о показателях свойств, содержащуюся в справочной литературе.
Метрологические службы федеральных органов исполнительной власти и юридических лиц могут создаваться в министерствах (ведомствах), организациях, на предприятиях и в учреждениях, являющихся юридическими лицами для выполнения работ по обеспечению единства и требуемой точности измерений, осуществления метрологического контроля и надзора.
При выполнении работ в сферах, предусмотренных ст. 13 Закона РФ от 27.04.93 № 4871-1 "Об обеспечении единства измерений", создание МС для обеспечения единства измерений является обязательным. Так, МС созданы в Минздраве, Минатоме, Минприроде, Миноборонпроме и других федеральных органах исполнительной власти. МС функционируют в РАО ЕЭС России, РАО "Газпром", НК ЮКОС, НК "Лукойл". Права и обязанности МС определяются положениями о них, утверждаемыми руководителями органов управления или юридических лиц.
Если на достаточно крупных предприятиях (в законодательно утвержденных сферах) организуются полноценные МС, то на небольших предприятиях Госстандарт рекомендует назначать лиц, ответственных за обеспечение единства измерений. Для ответственных лиц утверждается должностная инструкция, в которой устанавливаются их функции, права, обязанности и ответственность.
ГМС России в своей деятельности учитывает документы международных региональных организаций по метрологии.
Вопросы для самопроверки
1) Что такое метрология?
2) Какие разделы метрологии вы знаете?
3) В чем заключается смысл основного уравнения измерений?
4) Дайте определение понятию «физическая величина».
5) Что характеризуют понятия размерность и размер физической величины?
6) Какая система единиц величин принята к использованию в Российской Федерации?
7) Что такое метод измерений? Какие методы вы знаете?
8) Какие характеристики отражают понятие «качество измерений»?
9) Каким документом регламентированы характеристики погрешности измерений и формы их представления?
10) Приведите уравнение модели для оценивания общей погрешности измерений.
11) Какие характеристики средств измерений называют метрологическими?
12) Что означает понятие «единство измерений»?
13) Что устанавливает Закон «Об обеспечении единства измерений»?
14) Перечислите субъекты метрологии, входящие в Государственную метрологическую службу.
15) Назовите виды Государственного метрологического контроля и надзора. В каких сферах они действуют?
16) Что такое поверка и какие средства измерений подлежат поверке?
17) Кому предоставляют право применения знака "Ф" о соответствии количества фасованных товаров в упаковках установленным требованиям?
Содержание
Часть 1. Метрология
1 Метрология как деятельность
2 Метрология – наука об измерениях
2.1 Основные положения. Термины и определения
2.2 Измеряемые свойства и их меры
2.3 Физические величины. Единицы физических величин. Международная система единиц
2.4 Измерение физических величин. Классификация видов и методов измерений. Результаты измерений
2.5 Погрешности измерений
2.6 Последовательность и содержание операций при проведении измерений
2.7 Средства измерений, основные понятия и классификация. Метрологические характеристики средств измерений
3 Обеспечение единства измерений
3.1 Государственная система обеспечения единства измерений
3.2 Государственный метрологический контроль и надзор
Вопросы для самопроверки
Часть I. метрология
Метрология как деятельность
Обеспечение качества - одно из приложений метрологии как практической. В общем же случае метрология играет и познавательную, и созидательную роль в жизни общества.
Измерения осуществлялись и развивались от глубокой древности до наших дней.
Измерительные технологии применяются во всех без исключения сферах деятельности человека:
от торговли до навигации, здравоохранения и биологии;
от криминалистики и экологии до фундаментальных наук и промышленного производства;
от психофизиологии до землепользования, агротехники и разведки природных ресурсов.
В той или иной форме измерениями занимается практически всё население планеты. Или, другими словами, нет такой сферы общественной жизни, которая была бы свободна от измерений. Почти невозможно выбрать объект не доступный измерению.
Давно известно, что развитие теорий и их практическое применение немыслимы без первичной информации, получаемой путём измерений в процессе научного познания. Измерения распространены также как и математические методы и вычисления. И метрология, и математика рождались, развивались в тесной взаимосвязи. Но в силу отличительных особенностей у метрологии есть и своё место в науке.
Во-первых, получение достоверной измерительной информации немыслимо без привлечения арсенала метрологии. Это и методические приёмы по измерению, обработке результатов измерений, по оценке достоверности полученных результатов. Т.е. вся технология получения достоверной первичной информации о свойствах исследуемых объектов или явлений.
Во-вторых, многоплановая социальная значимость обеспечения единства измерений - было и остаётся естественной государственной монополией и осуществляется при поддержке и под надзором государственных органов управления.
В-третьих, метрология взаимосвязана в общей системе наук. Теория измерений имеет все признаки математической дисциплины. Методы измерений, воспроизведение единиц величин и шкал прочно связаны с естественными науками (физика, химия...). Прикладная метрология использует достижения технических дисциплин в области приборостроения. Законодательная метрология имеет признаки юриспруденции.
Таким образом, результаты измерений, получаемые от метрологической деятельности:
составляют объективную основу информации, необходимой для принятия решений и управления;
сопровождают каждое новое открытие в науке, лежащее в основе физических или химических явлений, а также в других областях;
уточняют многие неправильные выводы и заключения, которые были сделаны ранее на основе наблюдений за явлениями природы;
широко применяются в технике, народном хозяйстве, торговле;
служат основой для управления технологическими процессами при изготовлении продукции;
служат основой для оценки качества продукции.
Массовость и значимость измерений определяют многообразие видов практической метрологической деятельности:
обеспечение единства измерений;
воспроизведение единиц величин;
передача информации о размерах единиц;
разработка и изготовление средств измерений;
поверка и калибровка средств измерений;
метрологическое обеспечение производства;
метрологическое обеспечение систем качества;
метрологическая экспертиза технической документации;
Государственный метрологический контроль и надзор
и другие.
Метрология - наука об измерениях
2.1 Основные положения. Термины и определения
Термин «метрология» произошел от греческих слов: mετρoν- мера и loγoς– учение, слово. Но это лишь первичный смысл данного понятия.
Вплоть до 20 века содержание метрологии носило справочно-описательный характер: «метрология есть описание всякого рода мер по их наименованиям, подразделениям и взаимным отношениям» (Петрушевский Ф.И., 1849г.).
Современная метрология, опирающаяся на достижения различных наук, их методы и технические средства, в свою очередь, способствующая развитию наук, сама стала наукой в современном понимании этого слова:
метрология - наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Основные термины и определения, используемые в метрологии в настоящее время, приведены в документе Рекомендации РМГ 29-99 «ГСИ. Метрология. Основные термины и определения».
Различают: теоретическую, законодательную и прикладную метрологию.
Теоретическая метрология - раздел метрологии, предметом которого является разработка фундаментальных основ метрологии. Теоретическая метрология занимается изучением фундаментальных вопросов теории измерений и включает: основные понятия и термины; учение о физических величинах; теорию единства измерений; теорию построения СИ; теорию точности измерений (теория погрешностей СИ, теория методов измерений; методы обработки измерительной информации).
Законодательная метрология- раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц физических величин, эталонов, методов и средств измерений, направленных на обеспечение единства и необходимой точности измерений в интересах общества. Нормативной основой обеспечения единства измерений в РФ является Государственная система обеспечения единства измерений (ГСИ), сформированная в виде межотраслевого комплекса нормативных документов, устанавливающих соответствующие правила и нормы, утверждаемые Федеральным органом исполнительной власти в области технического регулирования и метрологии. Общие положения, цель, задачи и состав ГСИ определяет национальный стандарт ГОСТ Р 8.000-2000 «Государственная система обеспечения единства измерений. Основные положения».
Практическая (прикладная) метрология посвящается изучению и решению вопросов практического применения разработок теоретической метрологии и положений законодательной метрологии. К ней относятся вопросы метрологического обеспечения. Под метрологическим обеспечением (МО) понимается установление и применение научных и организационных основ, технических средств, правил и норм, необходимых для достижения единства и требуемой точности измерений, а также качества измерений.
Основными понятиями в метрологии являются:
- измеряемая (в т.ч. физическая) величина;
- единица ФВ;
- измерение;
- погрешность измерений;
- метод измерений;
- средство измерений;
- условия измерений.
Дата: 2019-07-30, просмотров: 251.
