Прежде чем исправить одиночную ошибку в принятой комбинации из п разрядов, необходимо определить, какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенном разряде соответствуют свой класс вычетов и свой опознаватель. Так как в циклическом коде опознавателями ошибок являются остатки от деления многочленов ошибок на образующий многочлен кода g ( x ), то g ( x ) должно обеспечить требуемое число различных остатков при делении векторов ошибок с единицей в искаженном разряде. Как отмечалось, наибольшее число остатков дает неприводимый многочлен. При степени многочлена m = n-k он может дать 2n-k - 1 ненулевых остатков (нулевой остаток является опознавателем безошибочной передачи).
Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравенства
2 n - k - 1 ³ 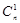 = n ,
= n ,
где 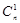 - общее число разновидностей одиночных ошибок в кодовой комбинации из п символов; отсюда находим степень образующего многочлена кода
- общее число разновидностей одиночных ошибок в кодовой комбинации из п символов; отсюда находим степень образующего многочлена кода
m = n – k ³ log 2 ( n +1)
и общее число символов в кодовой комбинации. Наибольшие значения k и п для различных m можно найти пользуясь табл. 4.13.
Таблица 4.13.
| M | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| N | 1 | 3 | 7 | 15 | 31 | 63 | 127 | 255 | 511 | 1023 |
| K | 0 | 1 | 4 | 11 | 26 | 57 | 120 | 247 | 502 | 1013 |
Как указывалось, образующий многочлен g ( x ) должен быть делителем двучлена х n +1. Доказано, что любой двучлен типа х2m-1+ 1 = хn+1 может быть представлен произведением всех неприводимых многочленов, степени которых являются делителями числа т (от 1 до т включительно). Следовательно, для любого т существует по крайней мере один неприводимый многочлен степени т, входящий сомножителем в разложение двучлена хn+1.
Пользуясь этим свойством, а также имеющимися в ряде книг таблицами многочленов, неприводимых при двоичных коэффициентах, выбрать образующий многочлен при известных n и m несложно. Определив образующий многочлен, необходимо убедиться в том, что он обеспечивает заданное число остатков.
Пример 35. Выберем образующий многочлен для случая n = 15 и m = 4.
Двучлен x15 + 1 можно записать в виде произведения всех неприводимых многочленов, степени которых являются делителями числа 4. Последнее делится на 1, 2, 4.
В таблице неприводимых многочленов находим один многочлен первой степени, а именно x+1, один многочлен второй степени x2 + x + 1 и три многочлена четвертой степени: х4 + x + 1, х4 + х3 + 1, х4 + х3 + х2 + х + 1. Перемножив все многочлены, убедимся в справедливости соотношения (х + 1)(х2 + х + 1)(х4 + х + 1)(х4 + х3+ 1)(х4 + х3 + х2 + х + 1) = x15 + 1
Один из сомножителей четвертой степени может быть принят за образующий многочлен кода. Возьмем, например, многочлен х4 + х3 + 1, или в виде двоичной последовательности 11001.
Чтобы убедиться, что каждому вектору ошибки соответствует отличный от других остаток, необходимо поделить каждый из этих векторов на 11001.Векторы ошибок m младших разрядов имеют вид: 00…000, 00…0010, 00…0100, 00…1000.
Степени соответствующих им многочленов меньше степени образующего многочлена g(x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий вектору ошибки в следующем старшем разряде, получаем при делении 00...10000 на 11001, т.е.
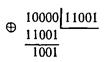
Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g(x) комбинацию в виде единицы с рядом нулей и выписывая все промежуточные остатки:

При последующем делении остатки повторяются.
Таким образом, мы убедились в том, что число различных остатков при выбранном g(x) равно п = 15, и, следовательно, код, образованный таким g(x), способен исправить любую одиночную ошибку. С тем же успехом за образующий многочлен кода мог быть принят и многочлен х4 + х + 1. При этом был бы получен код, эквивалентный выбранному.
Однако использовать для тех же целей многочлен х4 + х3 + x2 + х + 1 нельзя. При проверке числа различных остатков обнаруживается, что их у него не 15, а только 5. Действительно,
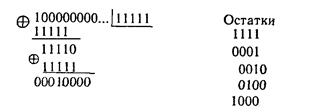
Это объясняется тем, что многочлен x4 + х3 + х2 + х + 1 входит в разложение не только двучлена x15+ 1, но и двучлена x5 + 1.
Из приведенного примера следует, что в качестве образующего следует выбирать такой неприводимый многочлен g ( x ) (или произведение таких многочленов), который, являясь делителем двучлена хп + 1, не входит в разложение ни одного двучлена типа хλ+ 1, степень которого λ меньше п. В этом случае говорят, что многочлен g ( x ) принадлежит показателю степени п.
В табл. 4.14 приведены основные характеристики некоторых кодов, способных исправлять одиночные ошибки или обнаруживать все одиночные и двойные ошибки.
Таблица 4.14.
| Показатель неприводимого многочлена | Образующий многочлен | Число остатков | Длина кода |
| 2 3 3 4 4 5 5 | x2 + x + 1 x3 + x + 1 x3 + x2 + 1 x4 + x3 + 1 x4 + x + 1 x5 + x2 + 1 x5 + x3 + 1 | 3 7 7 15 15 31 31 | 3 7 7 15 15 31 31 |
Это циклические коды Хэмминга для исправления одной ошибки, в которых в отличие от групповых кодов Хэмминга все проверочные разряды размещаются в конце кодовой комбинации.
Эти коды могут быть использованы для обнаружения любых двойных ошибок. Многочлен, соответствующий вектору двойной ошибки, имеет вид ξ(х) = х i – х j , или ξ(x) = х i (х j – i + 1) при j>i. Так как j – i<n, a g ( x ) не кратен х и принадлежит показателю степени п, то ξ(x) не делится на g ( x ), что и позволяет обнаружить двойные ошибки.
Дата: 2019-07-30, просмотров: 332.