Все формулы алгебры логики делятся на три класса: тавтологии (тождественно истинные),тождественно ложные, выполнимые.

Формулу А называют тождественно истинной, если она при всех значениях входящих в неё переменных высказываний принимает значение 1(истина). Формулу А называют тождественно ложной, если она при всех значениях входящих в неё переменных принимает значение 0(ложь).Формулу A называют выполнимой, если она принимает значение 1(истина), хотя бы на одном наборе входящих в нее переменных и не является тождественно истинной.

Вопрос к какому классу формул относится текущая формула A и называется проблемой разрешимости. Эта проблема решается элементарно с помощью таблицы истинности, однако для больших формул таблицы очень громоздки и их использование затруднительно.

Другой способ основан на приведение формулы A к КНФ (конъюнктивная нормальная формула) или ДНФ (дизъюнктивная) и использовании специального алгоритма, который позволяет определить является ли данная формула тождественно истинной или не является. Одновременно с этим решается проблема разрешимости.

Механизм применения вышеназванного алгоритма таков. Сначала он применяется к формуле A. Если A 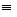1 то задача решена. Если это не так, то алгоритм применяется к формуле A Если A 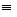1 то A 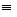0 и задача решена. Если это не так, то A - выполнимая формула.

Механизм установления тождественной истинности формулы A основан на следующих теоремах.

 Теорема 3. Для того, чтобы элементарная дизъюнкция (сумма переменных и их отрицаний) была тождественно истинной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание ( x_i v x_i 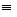1)

Теорема 4. Для того, чтобы элементарная конъюнкция (произведение переменных и их отрицаний) была тождественно ложной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание.

( x_i ^ x_i 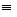0)

Теорема 5. Для того, чтобы формула алгебры логики A была тождественно истинна, необходимо и достаточно, чтобы каждая элементарная дизъюнкция, входящая в КНФ (конъюктивная нормальная форма – произведение элементарных сумм (дизъюнкций)) A, содержала переменную и ее отрицание. Доказательство:

Необходимо. Пусть A 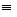1 Тогда КНФ A 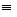1 и КНФA 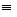A₁ ^A₂ ^A₃ ^...^A_n ^ 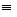1 -> ^V₁=(1,n), A_i 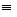1

Так как A_i - элементарная дизъюнкция, то по теореме 3 A_i содержит переменную и ее отрицание.

Достаточно. Пусть A_i - содержит переменную и ее отрицание. Тогда по теореме 3 A_i 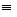1, i=(1,n) Но 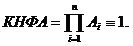Следовательно A- тождественно истинная формула.

Теорема 6. Для того, чтобы формула алгебры логики A была тождественно ложной, необходимо и достаточно, чтобы каждая элементарная конъюнкция, входящая в ДНФ (дизъюнктивная нормальная форма сумма элементарных произведений (конъюнкций)) A, содержала переменную и ее отрицание.

Примеры. A=((xy) -> x) ^ (xy -> y) Получить СДНФ и СКНФ с помощью таблицы истинности и путем элементарных преобразований

Основные логические выводы

Вывод – это процедура получения нового высказывания на основе одного или более уже принятых высказываний.

Правило вывода – это рецепт, предписание, позволяющее из признанных за истинные высказываний одной схемы (посылок) получить и признать за истинное некоторое высказывание другой схемы (заключение).

Вывод, соответствующий правилу вывода, называется правильным. Формулирование правил вывода – не менее важная задача логики, чем нахождение и отбор логических законов.

Важнейшей характеристикой вывода является отношение совместимости между его посылками и заключением. Не может быть выводом, например, связь высказываний, противоречащих друг другу. Отношение совместимости может быть взято в качестве основания классификации выводов.

Выводы подразделяются на дедуктивные и недедуктивные. В дедуктивных выводах между посылками (их конъюнкцией) и заключением имеет место отношение следования: не бывает так, что посылки истинны, а заключение ложно. В некоторых случаях отношение между посылками и заключениями характеризуется равнозначностью, т.е. не только из посылок следует заключение, но и из заключения следуют посылки.

При определении отношения следования (и, стало быть, дедуктивности вывода) можно использовать понятие логического закона: из конъюнкции посылок A следует заключение B , если и только если выражение A ® B – логический закон.

Истинность заключения в дедуктивном выводе гарантируется истинностью посылок. Знание, получаемое с его помощью, не может быть более общим, чем то, которое заложено в исходных посылках.

Вывод, в котором заключение не следует из посылок, но, тем не менее, совместимо с ними, называется правдоподобным. Правила дедуктивных выводов в логике высказываний. С помощью правил вывода устанавливается зависимость логической структуры заключения от логической структуры посылок. В простейшем случае правило вывода можно записать в виде схемы, которая состоит из двух частей (верхней и нижней), разделенных горизонтальной чертой; причем над чертой в столбец будем выписывать логические схемы посылок, а под ней – заключения.

Схема правила вывода, в котором посылки имеют вид A₁ ,A₂ ,A₃ , ... , A_n, а заключение – B.

Правила дедуктивных выводов логики высказываний подразделяются на основные и производные. Основные правила являются более простыми. Их перечень можно составить так, чтобы, во-первых, они были содержательно очевидными (для этой цели можно воспользоваться определениями логических союзов), во-вторых, образованная из них система определяла бы все возможные правила выводов логики высказываний, т.е. чтобы система удовлетворяла требованию полноты. В рамках современной логики доказано, что для логики высказываний такая система правил существует.

Производные правила выводятся из основных правил. В сущности их можно признать излишними, так как можно обойтись и без них. Но их введение в систему зачастую сокращает процесс вывода. Производные правила, таким образом, играют вспомогательную роль.

Как основные, так и производные правила, в свою очередь, делятся на прямые и непрямые (косвенные). Прямыеправила вывода указывают на выводимость некоторых высказываний из других высказываний (заключений из посылок). Непрямые (косвенные) правила выводов дают возможность заключать о правомерности некоторых выводов из правомерности других выводов. Сначала рассмотрим основные прямые правила.