Цель работы: исследовать свойства и поведение динамических объектов, описываемых системами обыкновенных нелинейных дифференциальных уравнений, используя для их решения средства пакета MathCAD.

Последовательность выполнения работы

Согласно номеру по списку группы выбрать из табл.3.1. систему уравнений (первое и второе уравнение), описывающую исследуемый динамический объект.

Построить структурную схему для исследуемого динамического объекта, аналогичную приведенной на рис. 3.1.

Составить и отладить программу решения системы дифференциальных уравнений согласно Приложению 3.1.

Примечание. Интегрирование систем уравнений проводится на интервале от 0 до 2 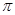.Начальные значения для  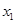в уравнениях, содержащих 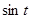, равны 0; в уравнениях, содержащих 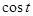, равны 1. Начальные значения для  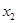для всех вариантов равны 0. Количество точек на интервале для первого расчета принять равным 8, для второго – 32.

Построить графики поведения динамического объекта для двух случаев (расчетов).

Сравнить поведение объектов для двух случаев (расчетов) и сделать вывод об изменении точности.

Номер по списку 5	Задание
	Первое уравнение 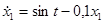; Второе уравнение ;

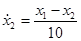Пояснительная записка

1) Выполняем пункт №1

2) Выполняем пункт №2. Анализируем структуру объекта, которая определяется интеграторами И₁ и И₂, сумматорами S_1, S₂, S_3, и S_4, линейно– усилительными блоками а₁₁ , а₁₂ , а₂₁ ,а₂₂ и системой связей между ними. Видим, что в нашем задании отсутствуют элементы а₁₂ и f₂. То есть отсутствуют один линейно– усилительный блок а₁₂ и внешнее (входное) воздействие f₂ на объект.

Структурная схема для исследуемого динамического объекта показана в файле 3zad_struktura.bmp.

3) Выполняем пункт №3.

Запускаем программу “Mathcad v11.0a.

Сохраняем созданный программой файл под именем 5_3_8.mcd (File->Save As…), в котором будем создавать листинг программы для выполнения 3 задания, где количество точек расчёта на интервале (t0, t1) равно восьми .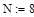

Ориентируясь на образец (Приложение 3.1) начинаем с клавиатуры вводить необходимые выражения, а также пользуясь манипулятором (мышь) для визуального выбора команд в нашей программе “Mathcad v11.0a”.

Чтобы ввести символ производной по времени, например, в выражении

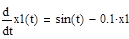
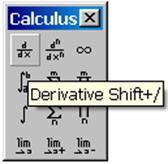
надо нажать пиктограмму 6 (см. рис. 1) в файле для задания №1 и после в окне выбрать указанный элемент.

Так как интегрирование систем уравнений проводится на интервале от 0 до 2 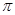, то задаём конечное значение независимой переменной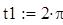

Начальное значения для 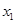 в уравнении, содержащем 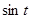, равны 0, то есть .

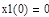При изменении содержания листинга программа автоматически пересчитывает все промежуточные результаты и ответ. Чтобы задать пересчёт всех формул на странице листинга выбираем команду в программе (Tools->Calculate-> Calculate Worksheet).

4) В этом же файле создаём таблицу S и графики.

Чтобы вставить таблицу S надо просто набрать её имя и нажать клавишу Enter.

В выражении 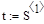 цифра в угловых скобках означает массив данных 1-го столбца таблицы (S).

Чтобы создать область для отображения графиков нажимаем пиктограмму 3 (см. Рис. 1) или вводим имя зависимой переменной (x1 или x2), а потом нажимаем символ @, то есть вводим выражение x1@ или x2@. В первом случае слева вводим имена зависимых переменных (x1 или x2), а снизу вводим независимую переменную (t). Также предусмотрено задание числового интервала по осям ОХ и OY для отображения графиков.

Аналогично проводим вычисления для N=32 и сохраняем листинг с результатами в другом файле 5_3_32.mcd.

5) При увеличении точности (N) гладкость графиков улучшается, но общее поведение объектов не изменяется.

То, что мы набрали (листинг программы) в рабочей области программы для N=8 и сохранили в файле 5_3_8.mcd можно просмотреть в файле 5_3_8.rtf.

То, что мы набрали (листинг программы) в рабочей области программы для N=32 и сохранили в файле 5_3_32.mcd можно просмотреть в файле 5_3_32.rtf.

Вывод: из полученных результатов видим, что вышеупомянутые зависимости нелинейны, что представлено графически.

Задание на контрольную работу

по дисциплине “Основы системного анализа объектов и процессов компьютеризации ”