Высокая точность взвешивания дозируемых материалов необходима для наиболее рационального их расхода и более точного соблюдения технологических операций. Это влияет на качество и себестоимость готовой продукции.
Кривые, получаемые при взвешивании и дозировании материалов, имеют сходство с кривыми измерения температуры в плане наличия локально-стационарного участка типа "полочки". Поэтому было произведено исследования алгоритма, работа которого основана на действии робастного фильтра, применительно к весовым кривым изменения сигнала. Исследование проводилось путем сравнения предлагаемого алгоритма с более простым - алгоритмом текущего среднего.
Выбор алгоритмов РЭС в качестве базовой процедуры оценивания объясняется следующими причинами:
ü достигается эффективное совмещение операций обнаружения и отбраковки выбросов (как операций проверки и повышения достоверности) с операциями собственно сглаживания, то есть выделения медленно меняющегося полезного сигнала и фильтрации, соответственно, высокочастотной составляющей измерительных помех;
ü настроечные коэффициенты РЭС сравнительно просто связать с содержательными технологическими характеристиками процессов и параметрами контролируемых сигналов; тем самым методики настройки РЭС удачно вписываются в концепцию описания желаемых свойств полезного сигнала по целевым (общесистемным) критериям и ограничениям, а результаты их применения оказываются хорошо интерпретируемыми;
Результаты обработки весовых кривых с использованием алгоритма текущего среднего представлены в таблице 5 и показаны графически на рисунке 7. Результаты обработки при помощи алгоритма робастной фильтрации сведены в таблицу 6 и показаны на рисунке8.
Сравнивая полученные при обработки кривых результаты видно, что использование сложного алгоритма позволяет более точно определять массу дозируемых материалов. Точность определения массы достигается за счет более точной и надежной обработки данных и выделений на весовых кривых локально-стационарного участка, по которому можно судить о действительной величине массы с достаточной объективностью.
Следовательно, при сравнении рассмотренных алгоритмов предпочтение следует отдавать более сложному и более надежному.
Таблица 4 – Весовая кривая измерения в цифровом виде
| t, мин | Значение массы m | t, мин | Значение массы m |
| 1 | 2 | 3 | 4 |
| 0 | 0.697 | 23 | 1.2 |
| 1 | 0.749 | 24 | 1.17 |
| 2 | 0.810 | 25 | 1.2 |
| 3 | 0.855 | 26 | 1.751 |
| 4 | 0.910 | 27 | 0.99 |
| 5 | 0.951 | 28 | 0.946 |
| 6 | 1.015 | 29 | 0.905 |
| 7 | 1.08 | 30 | 0.851 |
| 8 | 1.03 | 31 | 0.825 |
| 9 | 1.09 | 32 | 0.77 |
| 10 | 1.14 | 33 | 0.72 |
| 11 | 1.21 | 34 | 0.66 |
| 12 | 1.17 | 35 | 0.68 |
| 13 | 1.27 | 36 | 0.665 |
| 14 | 1.165 | 37 | 0.69 |
| 15 | 1.12 | 38 | 0.705 |
| 16 | 1.169 | 39 | 0.73 |
| 17 | 1.215 | 40 | 0.72 |
| 18 | 1.26 | 41 | 0.7 |
| 19 | 1.33 | 42 | 0.72 |
| 20 | 1.28 | 43 | 0.74 |
| 21 | 1.32 | 44 | 0.755 |
| 22 | 1.26 | 45 | 0.753 |
Таблица 5 – Результаты обработки весовой кривой по методу текущего среднего
| t, мин | Значение массы m при n=5 | Значение массы m при n=7 |
| 1 | 2 | 3 |
| 0 | 0.647 | 0.677 |
| 1 | 0.710 | 0.694 |
| 2 | 0.754 | 0.696 |
| 3 | 0.804 | 0.693 |
| 4 | 0.855 | 0.680 |
| 5 | 0.908 | 0.677 |
| 6 | 0.962 | 0.669 |
| 7 | 0.997 | 0.661 |
| 8 | 1.033 | 0.667 |
| 9 | 1.071 | 0.689 |
| 10 | 1.110 | 0.719 |
| 11 | 1.130 | 0.759 |
| 12 | 1.196 | 0.805 |
| 13 | 1.211 | 0.855 |
| 14 | 1.207 | 0.910 |
| 15 | 1.199 | 0.950 |
| 16 | 1.208 | 0.99 |
| 17 | 1.186 | 1.031 |
| 18 | 1.219 | 1.074 |
| 19 | 1.251 | 1.105 |
| 20 | 1.281 | 1.156 |
| 21 | 1.290 | 1.168 |
| 22 | 1.278 | 1.186 |
| 23 | 1.246 | 1.192 |
| 24 | 1.214 | 1.203 |
| 25 | 1.160 | 1.210 |
| 26 | 1.106 | 1.233 |
| 27 | 1.055 | 1.220 |
| 28 | 1.002 | 1.246 |
| 29 | 0.949 | 1.262 |
| 30 | 0.903 | 1.260 |
| 31 | 0.859 | 1.240 |
| 1 | 2 | 3 |
| 32 | 0.814 | 1.200 |
| 33 | 0.765 | 1.159 |
| 34 | 0.731 | 1.105 |
| 35 | 0.699 | 1.055 |
| 36 | 0.683 | 1.005 |
| 37 | 0.680 | 0.955 |
| 38 | 0.698 | 0.905 |
| 39 | 0.708 | 0.858 |
| 40 | 0.719 | 0.811 |
| 41 | 0.721 | 0.773 |
| 42 | 0.725 | 0.739 |
| 43 | 0.723 | 0.716 |
| 44 | 0.728 | 0.699 |
| 45 | 0.735 | 0.696 |
Таблица 6 – Результаты обработки весовой кривой робастным алгоритмом
| t, мин | Скорость изменения показаний, кг/с | Значение массы m |
| 1 | 2 | 3 |
| 0 | 4.00 | 0.57 |
| 1 | 5.00 | 0.66 |
| 2 | 6.00 | 0.76 |
| 3 | 6.4 | 0.84 |
| 4 | 6.46 | 0.90 |
| 5 | 6.24 | 0.96 |
| 6 | 6.21 | 1.02 |
| 7 | 6.17 | 1.08 |
| 8 | 5.17 | 1.09 |
| 9 | 4.62 | 1.11 |
| 10 | 4.38 | 1.15 |
| 11 | 4.52 | 1.20 |
| 12 | 3.74 | 1.21 |
| 13 | 4.74 | 1.30 |
| 14 | 3.74 | 1.29 |
| 15 | 2.74 | 1.28 |
| 16 | 1.74 | 1.26 |
| 17 | 1.18 | 1.25 |
| 18 | 1.18 | 1.26 |
| 19 | 1.76 | 1.30 |
| 20 | 1.38 | 1.30 |
| 21 | 1.45 | 1.32 |

Рисунок 7 – Результаты обработки кривой методом текущего среднего
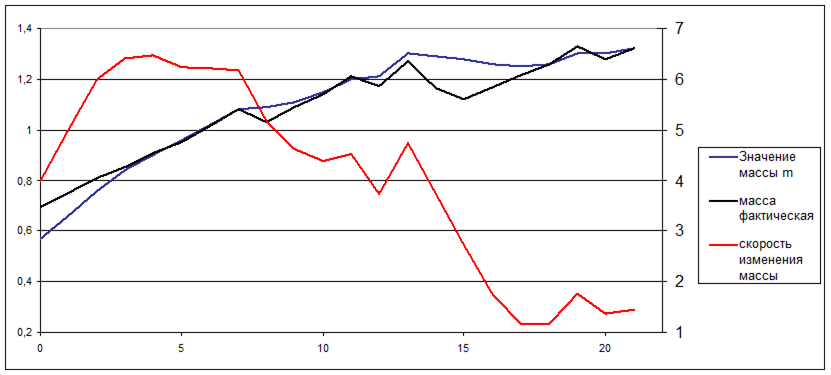
Рисунок 8 – Результаты обработки весовой кривой методом робастной фильтрации
Дата: 2019-07-30, просмотров: 297.