Эмпирическое исследование становления самосознания у детей, воспитывающихся вне семьи проводилось по схеме, представленной в алгоритме 1 (см. приложение1).

1.«Сырые» эмпирические данные по самооценке, взаимооценке и рефлексивной оценке были представлены в упорядоченном виде (см. табл. 1 и 2 приложения1)

По каждой шкале было высчитано среднее арифметическое значение признаков (оценка математического ожидания). Оно вычисляется по формуле:

,

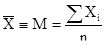где 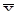- каждое наблюдаемое явление признака;

  i - индекс, указывающий на порядковый номер данного значения признака;

  n – количество наблюдений;

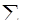- знак суммирования.

Числовые значения  по каждому показателю представлены в сводной матрице составляющих самосознания (см. табл. 3 приложения1). На их основании была выведена суммарная средняя оценка, характеризуемая как «Я- концепция» (табл.3 приложения1).

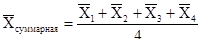
Этот показатель характеризуется как основной, интегрирующий эмпирический материал

исследования. Полученное значение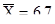

Графическое представление данного ряда (рис.1) характеризует его как непараметрический.

Во-первых, это видно визуально (в представленном ряду недостаточно низких значений, и поэтому он не может быть представлен кривой нормального распределения).

Во-вторых, при расчете 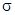 (среднеквадратичного отклонения) по формуле:

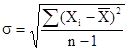
- было получено значение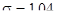

Как известно в практике исследований, часто берутся границы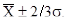

При полученном значении 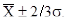=0,69 ,что соответствует значениям 6,01 – 6,7 – 7,39 , а это соответствует лишь – 29,6% от исследуемой выборки: вместо 50% при нормальном распределении.

В-третьих показатель асимметрии (А), высчитываемый по формуле:

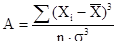 , отличен от нуля (А=0 при симметричных распределениях)

А = - 0,029 , что свидетельствует о левосторонней (положительной) асимметрии в распределении признака.

На основании вышеизложенного исследователь решает перейти на методы непараметрической статистики.

2. При обработке ряда, не имеющего признаков нормального распределения, иначе – непараметрического ряда – для величины, которая выражала бы его центральную тенденцию, более всего пригодна медиана, т.е. величина, расположенная в середине ряда. Её определяют по срединному рангу по формуле:

,

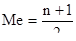где Ме – означает медиану,

  n – как в ранее приводившихся формулах – число членов ряда.

Изучаемый нами ряд имеет 27 членов. В проранжированном виде он представлен в табл.3.1. приложения.

Его ранговая медиана равна:

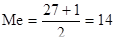 ,что соответствует величине 6,8 (по обе стороны данной величины находятся по 50% величин ряда)

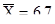(оценка математического ожидания).

3. Характеристика распределения численностей в исследуемом ряду получается из отношения его квартилей. Квартиль первая – её обозначение Q1 вычисляется по формуле:

,

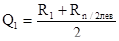это полусумма первого и последнего рангов первой – левой от медианы половины ряда; квартиль третья, обозначаемая 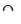, вычисляется по формуле:

,

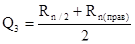т.е. как полусумма первого и последнего рангов второй, правой от медианы, половины ряда. Берутся порядковые значения рангов по их последовательности в ряду. В обрабатываемом ряду:

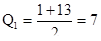
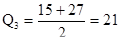
Рангу 7 , соответствует величина – 5,8

Рангу 21, соответствует величина – 7,4.

Для характеристики распределения в исследуемом непараметрическом ряду вычисляется среднее квартильное отклонение, обозначаемое Q.

Формула для Q такова:

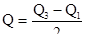
Для исследуемого ряда:

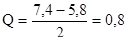
Полученные данные: Me = 6,8 и Q = 0,8 статистически описывают исследуемый непараметрический ряд, относящийся к шкале порядка.

В связи с тем, что полученное значение Me = 6,8 незначительно отличается от 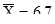, то исследователь оставляет за собой право изучения представленной совокупности по среднему значению признака.

4. Все представленные выше показатели характеризуют исследуемую совокупность по фактору самосознания в общем, виде. Однако, в представленном исследовании этого недостаточно. Необходимо дополнительно подтвердить, что:

1) представленные данные подобраны неслучайно;

2) в результате действия каких-либо факторов произошли достоверные изменения («сдвиги») в измеряемых показателях;

3) между измеряемыми признаками существуют определённые связи.

Исходя из проведённых исследований, мы можем утверждать, что предъявленные психометрические методики (самооценки, взаимооценки и рефлексивной оценки) принадлежат к особой категории структурных сдвигов исследуемого признака. Благодаря этому мы можем сопоставлять между собой показатели одних и тех же испытуемых по разным признакам, так как они измерены в одних и тех же единицах, по одной и той же шкале. В принципе, мы могли бы для такого рода «перепадов» использовать критерии оценки достоверности в средних тенденциях для независимых выборок: U – критерий Манна-Уитни, Q – критерий Розенбаума и 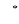 критерий - угловое преобразование Фишера. Однако, строго говоря, перед нами в исследовании – зависимые ряды значений, поскольку они измерены на одних и тех же испытуемых, поэтому будет более обоснованным использовать критерии оценки достоверности сдвигов для связанных выборок. Поэтому для сопоставления составляющих самооценки применяем критерий 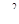Фридмана.

Данный критерий позволяет установить, что величины показателей самооценки (табл.1.1.приложения1) от показателя к показателю изменяются.

Проранжируем полученные по десяти показателям самооценки каждым испытуемым (см. табл. 1.1. приложения1).

Сумма рангов по каждому испытуемому должна составлять – 55. Расчётная общая сумма рангов в критерии определяется по формуле:

,

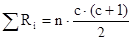где n – количество испытуемых;

c – количество условий измерения (замеров).

В данном случае,

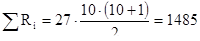(см.табл.1.1.)

Общая эмпирическая сумма рангов составляет:

152,5+117+130,5+136,5+149+146,5+177,5+169,5+155,5+150,5=1485,что совпадает с расчётной величиной.

Сформулируем гипотезы:

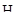: Различия в показателях самооценки, при каждом из 10 измерений, являются случайными.

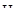: Различия в показателях самооценки, при каждом из 10 измерений, не являются случайными.

Теперь нам нужно определить эмпирическое значение 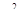 по формуле:

,

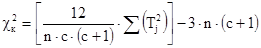где с - количество условий;

n – количество испытуемых;

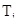- суммы рангов по каждому из условий.

Определим 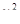 для данного случая:

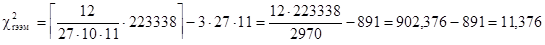
Поскольку в данном примере рассматривается десять измерений, то есть10 условий, с =10. Количество испытуемых n = 27. Это заставляет нас использовать критические значения 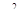,поскольку при больших n  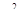имеет распределение, сходное с распределением 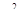, а существующие таблицы 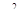предназначены только для 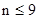. Количество степеней свободы  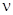определим по формуле:

,

где с – количество условий.

По специальной таблице критических значений (70) определяем критические значения критерия 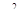 при данном числе степеней свободы .

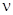Для :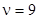  

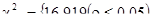
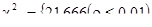
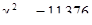
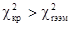
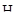принимается.

Ответ: 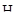принимается. Различия в показателях самооценки при каждом из десяти измерений являются случайными.